
Accessible category
Encyclopedia
The theory of accessible categories was introduced in 1989 by mathematicians Michael Makkai
and Robert Paré in the setting of category theory
. While the original motivation came from model theory
, a branch of mathematical logic
, it turned out that accessible categories have applications in homotopy theory. Some properties of accessible categories depend on the set universe in use, particularly on the cardinal
properties.
 be an infinite regular cardinal
be an infinite regular cardinal
and let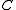 be a category
be a category
.
An object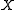 of
of 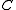 is called
is called  -presentable if the Hom functor
-presentable if the Hom functor
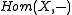 preserves
preserves 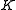 -directed colimits.
-directed colimits.
The category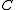 is called
is called 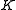 -accessible provided that :
-accessible provided that :
A category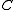 is called accessible if
is called accessible if 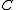 is
is 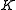 -accessible for some infinite regular cardinal
-accessible for some infinite regular cardinal 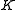 .
.
A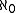 -presentable object is usually called finitely presentable, and
-presentable object is usually called finitely presentable, and
an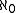 -accessible category is often called finitely accessible.
-accessible category is often called finitely accessible.
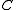 is cocomplete,
is cocomplete, 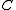 is called a locally presentable category.
is called a locally presentable category.
Locally presentable categories are also complete
.
Michael Makkai
Michael Makkai is a Canadian mathematician, specializing in mathematical logic. He works in model theory, category theory, algebraic logic, and in the theory of topoi. He graduated from the Eötvös Loránd University, Budapest, then worked at the Mathematical Institute of the Hungarian Academy of...
and Robert Paré in the setting of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. While the original motivation came from model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, it turned out that accessible categories have applications in homotopy theory. Some properties of accessible categories depend on the set universe in use, particularly on the cardinal
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
properties.
Definition
Let be an infinite regular cardinal
be an infinite regular cardinalRegular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
and let
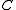 be a category
be a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
An object
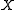 of
of 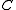 is called
is called  -presentable if the Hom functor
-presentable if the Hom functorHom functor
In mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.-Formal...
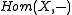 preserves
preserves 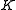 -directed colimits.
-directed colimits.The category
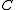 is called
is called 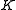 -accessible provided that :
-accessible provided that :
-
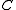 has
has  -directed colimits
-directed colimits -
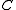 has a set
has a set 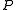 of
of 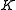 -presentable objects such that every object of
-presentable objects such that every object of 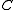 is a
is a 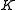 -directed colimit of objects of
-directed colimit of objects of 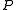
A category
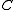 is called accessible if
is called accessible if 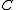 is
is 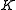 -accessible for some infinite regular cardinal
-accessible for some infinite regular cardinal 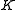 .
.A
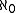 -presentable object is usually called finitely presentable, and
-presentable object is usually called finitely presentable, andan
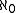 -accessible category is often called finitely accessible.
-accessible category is often called finitely accessible.Examples
- The category
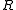 -Mod of (left)
-Mod of (left) 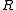 -modules is finitely accessible for any ring
-modules is finitely accessible for any ring 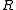 . The objects that are finitely presentable in the above sense are precisely the finitely presented modules (which are not necessarily the same class of objects than finitely generated modules unless
. The objects that are finitely presentable in the above sense are precisely the finitely presented modules (which are not necessarily the same class of objects than finitely generated modules unless 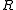 is noetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
is noetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
). - The category of simplicial setSimplicial setIn mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
s is finitely-accessible. - The category Mod(T) of models of some first-order theory T with countable signature is
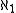 -accessible.
-accessible.  -presentable objects are models with a countable number of elements.
-presentable objects are models with a countable number of elements.
Further notions
When the category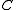 is cocomplete,
is cocomplete, 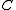 is called a locally presentable category.
is called a locally presentable category.Locally presentable categories are also complete
Complete category
In mathematics, a complete category is a category in which all small limits exist. That is, a category C is complete if every diagram F : J → C where J is small has a limit in C. Dually, a cocomplete category is one in which all small colimits exist...
.

