
Acoustic wave equation
Encyclopedia
In physics
, the acoustic wave equation governs the propagation of acoustic wave
s through a material medium. The form of the equation is a second order partial differential equation
. The equation describes the evolution of acoustic pressure or particle velocity
or particle velocity
u as a function of position r and time . A simplified form of the equation describes acoustic waves in only one spatial dimension, while a more general form describes waves in three dimensions.
. A simplified form of the equation describes acoustic waves in only one spatial dimension, while a more general form describes waves in three dimensions.
 ) as:
) as:
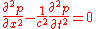
where is the acoustic pressure (the local deviation from the ambient pressure), and where
is the acoustic pressure (the local deviation from the ambient pressure), and where  is the speed of sound
is the speed of sound
.
 is a constant, not dependent on frequency (the dispersionless case), then the most general solution is
is a constant, not dependent on frequency (the dispersionless case), then the most general solution is
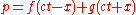
where and
and 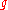 are any two twice-differentiable functions. This may be pictured as the superposition
are any two twice-differentiable functions. This may be pictured as the superposition
of two waveforms of arbitrary profile, one ( ) travelling up the x-axis and the other (
) travelling up the x-axis and the other ( ) down the x-axis at the speed
) down the x-axis at the speed  . The particular case of a sinusoidal wave travelling in one direction is obtained by choosing either
. The particular case of a sinusoidal wave travelling in one direction is obtained by choosing either  or
or 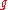 to be a sinusoid, and the other to be zero, giving
to be a sinusoid, and the other to be zero, giving
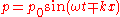 .
.
where is the angular frequency
is the angular frequency
of the wave and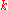 is its wave number.
is its wave number.
The equation of state (ideal gas law)

In an adiabatic process, pressure P as a function of density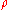 can be linearized to
can be linearized to

where C is some constant. Breaking the pressure and density into their mean and total components and noting that :
:
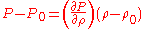 .
.
The adiabatic bulk modulus
for a fluid is defined as
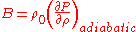
which gives the result
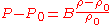 .
.
Condensation, s, is defined as the change in density for a given ambient fluid density.
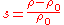
The linearized equation of state becomes
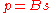 where p is the acoustic pressure(
where p is the acoustic pressure(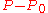 ).
).
The continuity equation
(conservation of mass) in one dimension is
Again the equation must be linearized and the variables split into mean and variable components.

Rearranging and noting that ambient density does not change with time or position and that the condensation multiplied by the velocity is a very small number:

Euler's Force equation (conservation of momentum) is the last needed component. In one dimension the equation is:
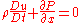 ,
,
where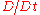 represents the convective, substantial or material derivative
represents the convective, substantial or material derivative
, which is the derivative at a point moving with medium rather than at a fixed point.
Linearizing the variables:
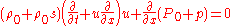 .
.
Rearranging and neglecting small terms, the resultant equation becomes:
 .
.
Taking the time derivative of the continuity equation and the spatial derivative of the force equation results in:
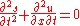
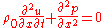 .
.
Multiplying the first by , subtracting the two, and substituting the linearized equation of state,
, subtracting the two, and substituting the linearized equation of state,
 .
.
The final result is

where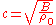 is the speed of propagation.
is the speed of propagation.
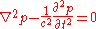
where is the Laplace operator
is the Laplace operator
,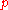 is the acoustic pressure (the local deviation from the ambient pressure), and where
is the acoustic pressure (the local deviation from the ambient pressure), and where  is the speed of sound
is the speed of sound
.
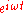 where
where 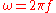 is the angular frequency
is the angular frequency
. The explicit time dependence is given by
Here is the wave number.
is the wave number.
where the asymptotic approximations to the Hankel functions, when , are
, are

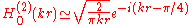 .
.
Depending on the chosen Fourier convention, one of these represents an outward travelling wave and the other an unphysical inward travelling wave. The inward travelling wave is only unphysical because of the singularity that occurs at r=0; inward travelling waves do exist.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the acoustic wave equation governs the propagation of acoustic wave
Acoustic wave
Acoustic waves are a type of longitudinal waves that propagate by means of adiabatic compression and decompression. Longitudinal waves are waves that have the same direction of vibration as their direction of travel. Important quantities for describing acoustic waves are sound pressure, particle...
s through a material medium. The form of the equation is a second order partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
. The equation describes the evolution of acoustic pressure
 or particle velocity
or particle velocityParticle velocity
Particle velocity is the velocity v of a particle in a medium as it transmits a wave. In many cases this is a longitudinal wave of pressure as with sound, but it can also be a transverse wave as with the vibration of a taut string....
u as a function of position r and time
 . A simplified form of the equation describes acoustic waves in only one spatial dimension, while a more general form describes waves in three dimensions.
. A simplified form of the equation describes acoustic waves in only one spatial dimension, while a more general form describes waves in three dimensions.Equation
Feynman derives the wave equation that describes the behaviour of sound in matter in one dimension (position ) as:
) as: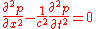
where
 is the acoustic pressure (the local deviation from the ambient pressure), and where
is the acoustic pressure (the local deviation from the ambient pressure), and where  is the speed of sound
is the speed of soundSpeed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
.
Solution
Provided that the speed is a constant, not dependent on frequency (the dispersionless case), then the most general solution is
is a constant, not dependent on frequency (the dispersionless case), then the most general solution is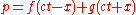
where
 and
and 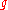 are any two twice-differentiable functions. This may be pictured as the superposition
are any two twice-differentiable functions. This may be pictured as the superpositionSuperposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of two waveforms of arbitrary profile, one (
 ) travelling up the x-axis and the other (
) travelling up the x-axis and the other ( ) down the x-axis at the speed
) down the x-axis at the speed  . The particular case of a sinusoidal wave travelling in one direction is obtained by choosing either
. The particular case of a sinusoidal wave travelling in one direction is obtained by choosing either  or
or 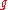 to be a sinusoid, and the other to be zero, giving
to be a sinusoid, and the other to be zero, giving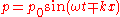 .
.where
 is the angular frequency
is the angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the wave and
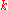 is its wave number.
is its wave number.Derivation
The wave equation can be developed from the linearized one-dimensional continuity equation, the linearized one-dimensional force equation and the equation of state.The equation of state (ideal gas law)

In an adiabatic process, pressure P as a function of density
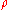 can be linearized to
can be linearized to
where C is some constant. Breaking the pressure and density into their mean and total components and noting that
 :
: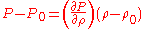 .
.The adiabatic bulk modulus
Bulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
for a fluid is defined as
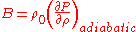
which gives the result
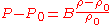 .
.Condensation, s, is defined as the change in density for a given ambient fluid density.
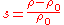
The linearized equation of state becomes
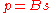 where p is the acoustic pressure(
where p is the acoustic pressure(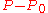 ).
).The continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
(conservation of mass) in one dimension is
-
 .
.
Again the equation must be linearized and the variables split into mean and variable components.

Rearranging and noting that ambient density does not change with time or position and that the condensation multiplied by the velocity is a very small number:

Euler's Force equation (conservation of momentum) is the last needed component. In one dimension the equation is:
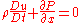 ,
,where
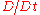 represents the convective, substantial or material derivative
represents the convective, substantial or material derivativeConvective derivative
The material derivative is a derivative taken along a path moving with velocity v, and is often used in fluid mechanics and classical mechanics...
, which is the derivative at a point moving with medium rather than at a fixed point.
Linearizing the variables:
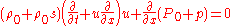 .
.Rearranging and neglecting small terms, the resultant equation becomes:
 .
.Taking the time derivative of the continuity equation and the spatial derivative of the force equation results in:
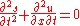
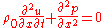 .
.Multiplying the first by
 , subtracting the two, and substituting the linearized equation of state,
, subtracting the two, and substituting the linearized equation of state, .
.The final result is

where
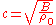 is the speed of propagation.
is the speed of propagation.Equation
Feynman derives the wave equation that describes the behaviour of sound in matter in three dimensions as: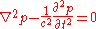
where
 is the Laplace operator
is the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
,
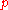 is the acoustic pressure (the local deviation from the ambient pressure), and where
is the acoustic pressure (the local deviation from the ambient pressure), and where  is the speed of sound
is the speed of soundSpeed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
.
Solution
The following solutions are obtained by separation of variables in different coordinate systems. They are phasor solutions, that is they have an implicit time-dependence factor of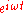 where
where 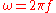 is the angular frequency
is the angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
. The explicit time dependence is given by

Here
 is the wave number.
is the wave number.Cylindrical coordinates
-
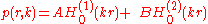 .
.
where the asymptotic approximations to the Hankel functions, when
 , are
, are
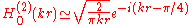 .
.Spherical coordinates
-
 .
.
Depending on the chosen Fourier convention, one of these represents an outward travelling wave and the other an unphysical inward travelling wave. The inward travelling wave is only unphysical because of the singularity that occurs at r=0; inward travelling waves do exist.
See also
- AcousticsAcousticsAcoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
- Wave EquationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
- Differential Equations
- ThermodynamicsThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
- Fluid DynamicsFluid dynamicsIn physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
- PressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
- Ideal Gas LawIdeal gas lawThe ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...

