Actuarial present value
Encyclopedia
In actuarial science
, the actuarial present value of a payment or series of payments which are random variable
s is the expected value
of the present value
of the payments, or equivalently, the present value of their expected values.
Actuarial present values are calculated for the payment or series of payments associated with life insurance
and life annuities
. In this case, the probability of a future payment is based on assumptions about the person's future mortality taking into account the person's age and an assumed life table
, while the present value of those future assumed payments depend upon the interest rate
(or rates) used to discount them for the passage of time.
The internal rate of return
of a contract is the rate of return
for which the actuarial present value of all cash flows is zero.
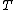be the future lifetime random variable
of an individual age x and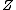
be the present value random variable of a whole life insurance
benefit of 1 payable at the instant of death.
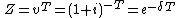
where i is the interest rate and δ is the equivalent force of interest.
To calculate the actuarial present value we need to calculate the expected value
of this random variable Z. For someone aged x this is denoted as 
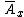in actuarial notation
. It can be calculated as
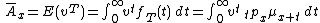
where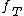
is the probability density function
of T,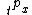
is the probability of a life age 
surviving to age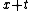 
and μ denotes force of mortality
.
The actuarial present value of an n-year term insurance policy can be found similarly by integrating from 0 to n.
The actuarial present value of an n year pure endowment
insurance benefit of 1 payable after n years if alive, can be found as
In practice the best information available about the random variable T is drawn from life table
s, which give figures by year. The actuarial present value of a benefit of 1 payable at the birthday after death would be
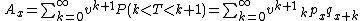
where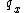
is the probability of death between the ages of 
and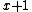 
.
In practice an insurance policy pays soon after death, which requires an adjustment of the formula.
of 1 per year paid continuously can be found in two ways:
Aggregate payment technique (taking the expected value
of the total present value
):
This is similar to the method for a life insurance policy. This time the random variable Y is the total present value random variable of the life annuity of 1 per year paid continuously as long as the person is alive, and is given by:
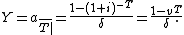
The expected value of Y is:
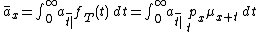
Current payment technique (taking the total present value of the function of time representing the expected values of payments):
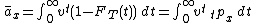
where F(t) is the cumulative distribution function
of the random variable T.
The equivalence follows also from integration by parts.
In practice life annuities are not paid continuously. If the payments are made at the end of each period the actuarial present value is given by
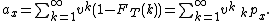
Keeping the total payment per year equal to 1, the longer the period, the smaller the present value is due to two effects:
Conversely, for contracts costing an equal lumpsum and having the same internal rate of return
, the longer the period between payments, the larger the total payment per year.
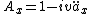
This is also commonly written as:
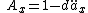
The formula also works equally well in the continuous case. In the case where the annuity and life insurance are not whole life, one should replace the insurance with an n-year endowment insurance (which can be expressed as the sum of an n-year term insurance and an n-year pure endowment), and the annuity with an n-year annuity due.
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
, the actuarial present value of a payment or series of payments which are random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the present value
Present value
Present value, also known as present discounted value, is the value on a given date of a future payment or series of future payments, discounted to reflect the time value of money and other factors such as investment risk...
of the payments, or equivalently, the present value of their expected values.
Actuarial present values are calculated for the payment or series of payments associated with life insurance
Life insurance
Life insurance is a contract between an insurance policy holder and an insurer, where the insurer promises to pay a designated beneficiary a sum of money upon the death of the insured person. Depending on the contract, other events such as terminal illness or critical illness may also trigger...
and life annuities
Life annuity
A life annuity is a financial contract in the form of an insurance product according to which a seller — typically a financial institution such as a life insurance company — makes a series of future payments to a buyer in exchange for the immediate payment of a lump sum or a series...
. In this case, the probability of a future payment is based on assumptions about the person's future mortality taking into account the person's age and an assumed life table
Life table
In actuarial science, a life table is a table which shows, for each age, what the probability is that a person of that age will die before his or her next birthday...
, while the present value of those future assumed payments depend upon the interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
(or rates) used to discount them for the passage of time.
The internal rate of return
Internal rate of return
The internal rate of return is a rate of return used in capital budgeting to measure and compare the profitability of investments. It is also called the discounted cash flow rate of return or the rate of return . In the context of savings and loans the IRR is also called the effective interest rate...
of a contract is the rate of return
Rate of return
In finance, rate of return , also known as return on investment , rate of profit or sometimes just return, is the ratio of money gained or lost on an investment relative to the amount of money invested. The amount of money gained or lost may be referred to as interest, profit/loss, gain/loss, or...
for which the actuarial present value of all cash flows is zero.
Life insurance
Let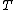 be the future lifetime random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
of an individual age x and
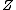be the present value random variable of a whole life insuranceWhole life insurance
Whole Life Insurance, or Whole of Life Assurance , is a life insurance policy that remains in force for the insured's whole life and requires premiums to be paid every year into the policy.-History:...
benefit of 1 payable at the instant of death.
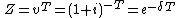
where i is the interest rate and δ is the equivalent force of interest.
To calculate the actuarial present value we need to calculate the expected value
of this random variable Z. For someone aged x this is denoted as 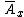in actuarial notationActuarial notation
Actuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.Traditional notation uses a halo system where symbols are placed as superscript or subscript before or after the main letter...
. It can be calculated as
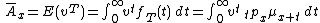
where
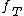is the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of T,
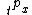is the probability of a life age surviving to age 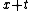and μ denotes force of mortalityForce of mortality
In actuarial science, force of mortality represents the instantaneous rate of mortality at a certain age measured on an annualized basis. It is identical in concept to failure rate, also called hazard function, in reliability theory....
.
The actuarial present value of an n-year term insurance policy can be found similarly by integrating from 0 to n.
The actuarial present value of an n year pure endowment
Endowment policy
An endowment policy is a life insurance contract designed to pay a lump sum after a specified term or on death. Typical maturities are ten, fifteen or twenty years up to a certain age limit...
insurance benefit of 1 payable after n years if alive, can be found as
In practice the best information available about the random variable T is drawn from life table
Life table
In actuarial science, a life table is a table which shows, for each age, what the probability is that a person of that age will die before his or her next birthday...
s, which give figures by year. The actuarial present value of a benefit of 1 payable at the birthday after death would be
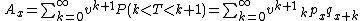
where
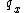is the probability of death between the ages of and 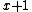.In practice an insurance policy pays soon after death, which requires an adjustment of the formula.
Life annuity
The actuarial present value of a life annuityLife annuity
A life annuity is a financial contract in the form of an insurance product according to which a seller — typically a financial institution such as a life insurance company — makes a series of future payments to a buyer in exchange for the immediate payment of a lump sum or a series...
of 1 per year paid continuously can be found in two ways:
Aggregate payment technique (taking the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the total present value
Present value
Present value, also known as present discounted value, is the value on a given date of a future payment or series of future payments, discounted to reflect the time value of money and other factors such as investment risk...
):
This is similar to the method for a life insurance policy. This time the random variable Y is the total present value random variable of the life annuity of 1 per year paid continuously as long as the person is alive, and is given by:
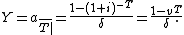
The expected value of Y is:
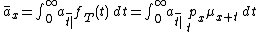
Current payment technique (taking the total present value of the function of time representing the expected values of payments):
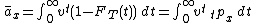
where F(t) is the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the random variable T.
The equivalence follows also from integration by parts.
In practice life annuities are not paid continuously. If the payments are made at the end of each period the actuarial present value is given by
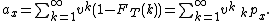
Keeping the total payment per year equal to 1, the longer the period, the smaller the present value is due to two effects:
- The payments are made on average half a period later than in the continuous case.
- There is no proportional payment for the time in the period of death, i.e. a "loss" of payment for on average half a period.
Conversely, for contracts costing an equal lumpsum and having the same internal rate of return
Internal rate of return
The internal rate of return is a rate of return used in capital budgeting to measure and compare the profitability of investments. It is also called the discounted cash flow rate of return or the rate of return . In the context of savings and loans the IRR is also called the effective interest rate...
, the longer the period between payments, the larger the total payment per year.
Life insurance as a function of the life annuity
The value of a life insurance can be derived from the value of a life annuity-due this way: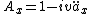This is also commonly written as:
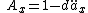
The formula also works equally well in the continuous case. In the case where the annuity and life insurance are not whole life, one should replace the insurance with an n-year endowment insurance (which can be expressed as the sum of an n-year term insurance and an n-year pure endowment), and the annuity with an n-year annuity due.
See also
- Actuarial scienceActuarial scienceActuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
- Actuarial notationActuarial notationActuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.Traditional notation uses a halo system where symbols are placed as superscript or subscript before or after the main letter...
- Actuarial reserveActuarial reservesAn actuarial reserve is a liability equal to the net present value of the future expected cash flows of a contingent event. In the insurance context an actuarial reserve is the present value of the future cash flows of an insurance policy and the total liability of the insurer is the sum of the...
- ActuaryActuaryAn actuary is a business professional who deals with the financial impact of risk and uncertainty. Actuaries provide expert assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms ....
- Force of mortalityForce of mortalityIn actuarial science, force of mortality represents the instantaneous rate of mortality at a certain age measured on an annualized basis. It is identical in concept to failure rate, also called hazard function, in reliability theory....
- Life tableLife tableIn actuarial science, a life table is a table which shows, for each age, what the probability is that a person of that age will die before his or her next birthday...
- Present valuePresent valuePresent value, also known as present discounted value, is the value on a given date of a future payment or series of future payments, discounted to reflect the time value of money and other factors such as investment risk...