Adaptive Huffman coding
Encyclopedia
Adaptive Huffman coding is an adaptive coding
technique based on Huffman coding
. It permits building the code as the symbols are being transmitted, having no initial knowledge of source distribution, that allows one-pass encoding and adaptation to changing conditions in data.
The benefit of one-pass procedure is that the source can be encoded in real time, though it becomes more sensitive to transmission errors, since just a single loss ruins the whole code.
-Gallager
-Knuth
) and Vitter
algorithm.
Numbers go down, and from right to left.
Weights must satisfy the sibling property, which states that nodes must be listed in the order of decreasing weight with each node adjacent to its sibling. Thus if A is the parent node of B and C is a child of B, then .
.
The weight is merely the count of symbols transmitted which codes are associated with children of that node.
A set of nodes with same weights make a block.
To get the code for every node, in case of binary tree we could just traverse all the path from the root to the node, writing down (for example) "1" if we go to the right and "0" if we go to the left.
We need some general and straightforward method to transmit symbols that are "not yet transmitted" (NYT). We could use, for example, transmission of binary numbers for every symbol in alphabet.
Encoder and decoder start with only the root node, which has the maximum number. In the beginning it is our initial NYT node.
When we transmit an NYT symbol, we have to transmit code for the NYT node, then for its generic code.
For every symbol that is already in the tree, we only have to transmit code for its leaf node.
For every symbol transmitted both the transmitter and receiver execute the update procedure:
Note: swapping nodes means swapping weights and corresponding symbols, but not the numbers.
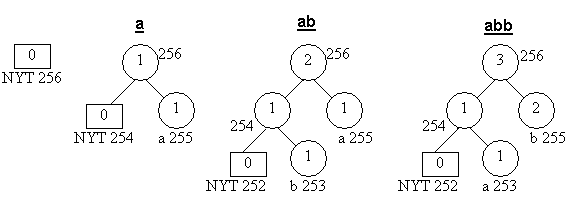
Start with an empty tree.
For "a" transmit its binary code.
NYT spawns two child nodes: 254 and 255.
Increase weight for root.
Code for "a", associated with node 255, is 1.
For "b" transmit 0 (for NYT node) then its binary code.
NYT spawns two child nodes: 252 for NYT and 253 for leaf node.
Increase weights for 253, 254, and root.
Code for "b" is 01.
For the second "b" transmit 01.
Go to that leaf node, 253. We have a block of weights of 1 and the biggest number in the block is 255, so swap the weights and symbols of nodes 253 and 255, increase weight, go to root, increase weight for root.
Future code for "b" is 1, and for "a" is now 01, which reflects their frequency.
Adaptive coding
Adaptive coding refers to variants of entropy encoding methods of lossless data compression. They are particularly suited to streaming data, as they adapt to localized changes in the characteristics of the data, and don't require a first pass over the data to calculate a probability model...
technique based on Huffman coding
Huffman coding
In computer science and information theory, Huffman coding is an entropy encoding algorithm used for lossless data compression. The term refers to the use of a variable-length code table for encoding a source symbol where the variable-length code table has been derived in a particular way based on...
. It permits building the code as the symbols are being transmitted, having no initial knowledge of source distribution, that allows one-pass encoding and adaptation to changing conditions in data.
The benefit of one-pass procedure is that the source can be encoded in real time, though it becomes more sensitive to transmission errors, since just a single loss ruins the whole code.
Algorithms
There are a number of implementations of this method, the most notable are FGK (FallerNewton Faller
Newton Faller the son of Kurt Faller and Ada Faller from Rio Grande do Sul, was a Brazilian computer scientist and electrical engineer. He is credited with the discovery of adaptive Huffman codes while an employee of IBM do Brasil in Rio...
-Gallager
Robert G. Gallager
Robert Gray Gallager is an American electrical engineer known for his work on information theory and communications networks. He was elected an IEEE Fellow in 1968 and a member of the National Academy of Engineering in 1979. He received the Claude E. Shannon Award from the IEEE Information Theory...
-Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
) and Vitter
Jeffrey Vitter
Jeffrey Scott Vitter is provost and executive vice chancellor and Roy A. Roberts Distinguished Professor at the University of Kansas in Lawrence, Kansas.-Education:...
algorithm.
Vitter algorithm
Code is represented as a tree structure in which every node has a corresponding weight and a unique number.Numbers go down, and from right to left.
Weights must satisfy the sibling property, which states that nodes must be listed in the order of decreasing weight with each node adjacent to its sibling. Thus if A is the parent node of B and C is a child of B, then
 .
.The weight is merely the count of symbols transmitted which codes are associated with children of that node.
A set of nodes with same weights make a block.
To get the code for every node, in case of binary tree we could just traverse all the path from the root to the node, writing down (for example) "1" if we go to the right and "0" if we go to the left.
We need some general and straightforward method to transmit symbols that are "not yet transmitted" (NYT). We could use, for example, transmission of binary numbers for every symbol in alphabet.
Encoder and decoder start with only the root node, which has the maximum number. In the beginning it is our initial NYT node.
When we transmit an NYT symbol, we have to transmit code for the NYT node, then for its generic code.
For every symbol that is already in the tree, we only have to transmit code for its leaf node.
For every symbol transmitted both the transmitter and receiver execute the update procedure:
- If current symbol is NYT, add two child nodes to NYT node. One will be a new NYT node the other is a leaf node for our symbol. Increase weight for the new leaf node and the old NYT and go to step 4. If not, go to symbol's leaf node.
- If this node does not have the highest number in a block, swap it with the node having the highest number, except if that node is its parent http://www.cs.duke.edu/csed/curious/compression/adaptivehuff.html#tree
- Increase weight for current node
- If this is not the root node go to parent node then go to step 2. If this is the root, end.
Note: swapping nodes means swapping weights and corresponding symbols, but not the numbers.
Example

Start with an empty tree.
For "a" transmit its binary code.
NYT spawns two child nodes: 254 and 255.
Increase weight for root.
Code for "a", associated with node 255, is 1.
For "b" transmit 0 (for NYT node) then its binary code.
NYT spawns two child nodes: 252 for NYT and 253 for leaf node.
Increase weights for 253, 254, and root.
Code for "b" is 01.
For the second "b" transmit 01.
Go to that leaf node, 253. We have a block of weights of 1 and the biggest number in the block is 255, so swap the weights and symbols of nodes 253 and 255, increase weight, go to root, increase weight for root.
Future code for "b" is 1, and for "a" is now 01, which reflects their frequency.

