Adaptive quadrature
Encyclopedia
In applied mathematics
, adaptive quadrature is a process in which the integral
of a function
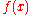is approximated
using static quadrature rules
on adaptively refined subintervals of the integration domain
. Generally, adaptive algorithms are just as efficient and effective as traditional algorithms for "well-behaved" integrands, but are also effective for "badly-behaved" integrands for which traditional algorithms fail.
1. procedure integrate ( f , a , b , tau )
2.
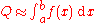
3.
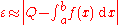
4. if
then
5. m = (a + b) / 2
6. Q = integrate(f,a,m,tau/2) + integrate(f,m,b,tau/2)
7. endif
8. return Q
An approximation
to the integral of 
over the interval 
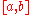is computed (line 2), as well as an error estimate 
(line 3). If the estimated error is larger than the required tolerance 
(line 4), the interval is subdivided (line 5) and the quadrature is applied on both halves separately (line 6). Either the initial estimate or the sum of the recursively computed halves is returned (line 7).
The important components are the quadrature
rule itself
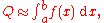
the error estimator
and the logic for deciding which interval to subdivide, and when to terminate.
There are, of course, several variants of this scheme. The most common will be discussed later.
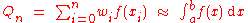
where the nodes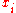
and weights 
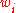are generally pre-computed.
In the simplest case, Newton–Cotes formulas of even degree are used, where the nodes
are evenly spaced in the interval:
.
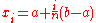When such rules are used, the points at which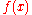
has been evaluated can be re-used upon recursion:
A similar strategy is used with Clenshaw–Curtis quadrature, where the nodes are chosen as
Or, when Fejér quadrature is used,
.
Other quadrature rules, such as Gaussian quadrature
or Gauss-Kronrod quadrature, may also be used.
An algorithm may elect to use different quadrature methods on different subintervals, for example using a high-order method only where the integrand is smooth.
See:
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, adaptive quadrature is a process in which the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
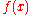is approximatedFunction approximation
The need for function approximations arises in many branches of applied mathematics, and computer science in particular. In general, a function approximation problem asks us to select a function among a well-defined class that closely matches a target function in a task-specific way.One can...
using static quadrature rules
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
on adaptively refined subintervals of the integration domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
. Generally, adaptive algorithms are just as efficient and effective as traditional algorithms for "well-behaved" integrands, but are also effective for "badly-behaved" integrands for which traditional algorithms fail.
General scheme
Adaptive quadrature follows the general scheme1. procedure integrate ( f , a , b , tau )
2.
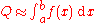
3.
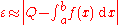
4. if
then5. m = (a + b) / 2
6. Q = integrate(f,a,m,tau/2) + integrate(f,m,b,tau/2)
7. endif
8. return Q
An approximation
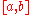to the integral of over the interval is computed (line 2), as well as an error estimate (line 3). If the estimated error is larger than the required tolerance (line 4), the interval is subdivided (line 5) and the quadrature is applied on both halves separately (line 6). Either the initial estimate or the sum of the recursively computed halves is returned (line 7).The important components are the quadrature
Quadrature
Quadrature may refer to:In signal processing:*Quadrature amplitude modulation , a modulation method of using both an carrier wave and a 'quadrature' carrier wave that is 90° out of phase with the main, or in-phase, carrier...
rule itself
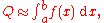
the error estimator
and the logic for deciding which interval to subdivide, and when to terminate.
There are, of course, several variants of this scheme. The most common will be discussed later.
Basic quadrature rules
The quadrature rules generally have the form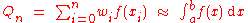where the nodes
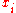and weights 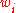are generally pre-computed.In the simplest case, Newton–Cotes formulas of even degree are used, where the nodes
are evenly spaced in the interval: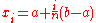.When such rules are used, the points at which
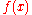has been evaluated can be re-used upon recursion:
A similar strategy is used with Clenshaw–Curtis quadrature, where the nodes are chosen as
Or, when Fejér quadrature is used,
.Other quadrature rules, such as Gaussian quadrature
Gaussian quadrature
In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
or Gauss-Kronrod quadrature, may also be used.
An algorithm may elect to use different quadrature methods on different subintervals, for example using a high-order method only where the integrand is smooth.
Error estimation
Some quadrature algorithms generate a sequence of results which should approach the correct value. Otherwise one can use a "null rule" which has the form of the above quadrature rule, but whose value would be zero for a simple integrand (for example, if the integrand were a polynomial of the appropriate degree).See:
- Richardson extrapolationRichardson extrapolationIn numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century. In the words of Birkhoff and Rota, ".....
(see also Romberg's methodRomberg's methodIn numerical analysis, Romberg's method is used to estimate the definite integral \int_a^b f \, dx by applying Richardson extrapolation repeatedly on the trapezium rule or the rectangle rule . The estimates generate a triangular array...
) - Null rules
- Epsilon algorithm
Subdivision logic
"Local" adaptive quadrature makes the acceptable error for a given interval proportional to the length of that interval. This criterion can be difficult to satisfy if the integrand are badly behaved at only a few points, for example with a few step discontinuities. Alternatively, one could require only that the sum of the errors on each of the subintervals be less than the user's requirement. This would be "global" adaptive quadrature. Global adaptive quadrature can be more efficient (using fewer evaluations of the integrand) but are generally more complex to program and may require more working space to record information on the current set of intervals.See also
- Adaptive Simpson's methodAdaptive Simpson's methodAdaptive Simpson's method, also called adaptive Simpson's rule, is a method of numerical integration proposed by G.F. Kuncir in 1962. It is probably the first recursive adaptive algorithm for numerical integration to appear in print, although more modern adaptive methods based on Gauss–Kronrod...
for an example of adaptive quadrature - QUADPACKQUADPACKQUADPACK is a FORTRAN 77 library for numerical integration of one-dimensional functions. It was included in the SLATEC Common Mathematical Library and is therefore in the public domain. The individual subprograms are also available on netlib....
, a FORTRAN library that uses global adaptive quadrature