Advantage (cryptography)
Encyclopedia
In cryptography
, an adversary's advantage is a measure of how successfully it can attack a cryptographic algorithm
, by distinguishing it from an idealized version of that type of algorithm. Note that in this context, the "adversary
" is itself an algorithm and not a person
. A cryptographic algorithm is considered secure if no adversary has a non-negligible
advantage, subject to specified bounds on the adversary's computational resources (see concrete security
). "Negligible" usually means "within O
(2-p)" where p is a security parameter
associated with the algorithm. For example, p might be the number of bits in a block cipher's key
.
for the function being studied, and let G be an oracle for an idealized function of that type. The adversary A is a probabilistic algorithm given F or G as input and which outputs 1 or 0. A's job is to distinguish F from G based on making queries to the oracle that it's given. We say:
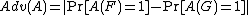
block cipher
. This cipher has 64-bit blocks and a 56-bit key. The key therefore selects one of a family of 256 permutation
s on the 264 possible 64-bit blocks. A "random DES instance" means our oracle F computes DES using some key K (which is unknown to the adversary) where K is selected from the 256 possible keys with equal probability.
We want to compare the DES instance with an idealized 64-bit block cipher, meaning a permutation selected at random from the (264)!
possible permutations on 64-bit blocks. Call this randomly selected permutation G. Note from Stirling's approximation
that (264)! is around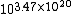
, so even specifying which permutation is selected requires writing down a number too large to represent exactly in any real computer. Viewed another way, G is an instance of a "cipher" whose "key length" is about 1021 bits, which again is too large to fit in a computer. (We can, however, implement G with storage space proportional to the number of queries, using a random oracle
).
Note that because the oracles we're given encrypt plaintext of our choosing, we're modelling a chosen-plaintext attack
or CPA, and the advantage we're calculating can be called the CPA-advantage of a given adversary. If we also had decryption oracles available, we'd be doing a chosen-ciphertext attack
or CCA and finding the CCA-advantage of the adversary.
We'll look at several different adversaries and see how they perform.
. It has its own DES implementation. It gives a single query to its oracle, asking for the 64-bit string of all zeroes to be encrypted. Call the resulting ciphertext E0. It then runs an exhaustive key search.
The algorithm looks like this:
E0 = oracle_query(0)
for k in 0,1,...,256-1:
if DESk(0) E0:
return 1
return 0
This searches the entire 56-bit DES keyspace and returns "1" if it probably finds a matching key. In practice, several plaintexts are required to confirm the key, as two different keys can result in one or more matching plaintext-ciphertext pairs. If no key is found, it returns 0.
If the input oracle is DES, this exhaustive search is certain to find the key, so Pr[A1(F)=1] = 1. If the input oracle is a random permutation, there are 264 possible values of E0, and at most 256 of them will get examined in the DES keysearch. So the probability of A1 returning 1 is at most 2-8. That is:
Pr[A1(G)=1] <= 2-8, so
Adv(A1) = |Pr[A1(F)=1] - Pr[A1(G)=1]| >= 1 - 2-8
so the advantage is at least about 0.996. This is a near-certain distinguisher, but it's not a security failure because it's no faster than brute force search--because it is brute force search.
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, an adversary's advantage is a measure of how successfully it can attack a cryptographic algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, by distinguishing it from an idealized version of that type of algorithm. Note that in this context, the "adversary
Adversary (cryptography)
In cryptography, an adversary is a malicious entity whose aim is to prevent the users of the cryptosystem from achieving their goal...
" is itself an algorithm and not a person
Person
A person is a human being, or an entity that has certain capacities or attributes strongly associated with being human , for example in a particular moral or legal context...
. A cryptographic algorithm is considered secure if no adversary has a non-negligible
Negligible
Negligible refers to the quantities so small that they can be ignored when studying the larger effect. Although related to the more mathematical concepts of infinitesimal, the idea of negligibility is particularly useful in practical disciplines like physics, chemistry, mechanical and electronic...
advantage, subject to specified bounds on the adversary's computational resources (see concrete security
Concrete security
In cryptography, concrete security or exact security is a practice-oriented approach that aims to give more precise estimates of the computational complexities of adversarial tasks than polynomial equivalence would allow....
). "Negligible" usually means "within O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(2-p)" where p is a security parameter
Security parameter
In cryptography, the security parameter is a variable that measures the input size of the problem. Both the resource requirements of the cryptographic algorithm or protocol as well as the adversary's probability of breaking security are expressed in terms of the security parameter.The security...
associated with the algorithm. For example, p might be the number of bits in a block cipher's key
Key (cryptography)
In cryptography, a key is a piece of information that determines the functional output of a cryptographic algorithm or cipher. Without a key, the algorithm would produce no useful result. In encryption, a key specifies the particular transformation of plaintext into ciphertext, or vice versa...
.
Description of concept
Let F be an oracleOracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
for the function being studied, and let G be an oracle for an idealized function of that type. The adversary A is a probabilistic algorithm given F or G as input and which outputs 1 or 0. A's job is to distinguish F from G based on making queries to the oracle that it's given. We say:
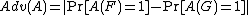
Examples
Let F be a random instance of the DESData Encryption Standard
The Data Encryption Standard is a block cipher that uses shared secret encryption. It was selected by the National Bureau of Standards as an official Federal Information Processing Standard for the United States in 1976 and which has subsequently enjoyed widespread use internationally. It is...
block cipher
Block cipher
In cryptography, a block cipher is a symmetric key cipher operating on fixed-length groups of bits, called blocks, with an unvarying transformation. A block cipher encryption algorithm might take a 128-bit block of plaintext as input, and output a corresponding 128-bit block of ciphertext...
. This cipher has 64-bit blocks and a 56-bit key. The key therefore selects one of a family of 256 permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s on the 264 possible 64-bit blocks. A "random DES instance" means our oracle F computes DES using some key K (which is unknown to the adversary) where K is selected from the 256 possible keys with equal probability.
We want to compare the DES instance with an idealized 64-bit block cipher, meaning a permutation selected at random from the (264)!
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
possible permutations on 64-bit blocks. Call this randomly selected permutation G. Note from Stirling's approximation
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
that (264)! is around
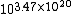, so even specifying which permutation is selected requires writing down a number too large to represent exactly in any real computer. Viewed another way, G is an instance of a "cipher" whose "key length" is about 1021 bits, which again is too large to fit in a computer. (We can, however, implement G with storage space proportional to the number of queries, using a random oracleRandom oracle
In cryptography, a random oracle is an oracle that responds to every query with a random response chosen uniformly from its output domain, except that for any specific query, it responds the same way every time it receives that query...
).
Note that because the oracles we're given encrypt plaintext of our choosing, we're modelling a chosen-plaintext attack
Chosen-plaintext attack
A chosen-plaintext attack is an attack model for cryptanalysis which presumes that the attacker has the capability to choose arbitrary plaintexts to be encrypted and obtain the corresponding ciphertexts. The goal of the attack is to gain some further information which reduces the security of the...
or CPA, and the advantage we're calculating can be called the CPA-advantage of a given adversary. If we also had decryption oracles available, we'd be doing a chosen-ciphertext attack
Chosen-ciphertext attack
A chosen-ciphertext attack is an attack model for cryptanalysis in which the cryptanalyst gathers information, at least in part, by choosing a ciphertext and obtaining its decryption under an unknown key. In the attack, an adversary has a chance to enter one or more known ciphertexts into the...
or CCA and finding the CCA-advantage of the adversary.
We'll look at several different adversaries and see how they perform.
Example 1: Guess at random
We'll call this adversary A0. It simply flips a coin and returns 1 or 0 with equal probability and without making any oracle calls. Thus, Pr[A0(F)=1] and Pr[A0(G)=1] are both 0.5. The difference between these probabilities is zero, so Adv(A0) is zero. The same thing applies if we always return 0, or always return 1: the probability is the same for both F and G, so the advantage is zero. This adversary can't tell F and G apart. If we're cipher designers, our desire (maybe not achievable) is to make it so that it's computationally infeasible for any adversary to do significantly better than this. We will have succeeded if we can make a cipher for which there's no distinguisher faster than brute force search.Example 2: Brute force search
This adversary (call it A1) will attempt to cryptanalyze its input by brute forceBrute force attack
In cryptography, a brute-force attack, or exhaustive key search, is a strategy that can, in theory, be used against any encrypted data. Such an attack might be utilized when it is not possible to take advantage of other weaknesses in an encryption system that would make the task easier...
. It has its own DES implementation. It gives a single query to its oracle, asking for the 64-bit string of all zeroes to be encrypted. Call the resulting ciphertext E0. It then runs an exhaustive key search.
The algorithm looks like this:
E0 = oracle_query(0)
for k in 0,1,...,256-1:
if DESk(0) E0:
return 1
return 0
This searches the entire 56-bit DES keyspace and returns "1" if it probably finds a matching key. In practice, several plaintexts are required to confirm the key, as two different keys can result in one or more matching plaintext-ciphertext pairs. If no key is found, it returns 0.
If the input oracle is DES, this exhaustive search is certain to find the key, so Pr[A1(F)=1] = 1. If the input oracle is a random permutation, there are 264 possible values of E0, and at most 256 of them will get examined in the DES keysearch. So the probability of A1 returning 1 is at most 2-8. That is:
Pr[A1(G)=1] <= 2-8, so
Adv(A1) = |Pr[A1(F)=1] - Pr[A1(G)=1]| >= 1 - 2-8
so the advantage is at least about 0.996. This is a near-certain distinguisher, but it's not a security failure because it's no faster than brute force search--because it is brute force search.