Ak singularity
Encyclopedia
In mathematics, and in particular singularity theory
an Ak, where k ≥ 0 is an integer
, describes a level of degeneracy of a function
. The notation was introduced by V. I. Arnold.
Let f : Rn → R be a smooth function
. We denote by Ω(Rn,R) the infinite-dimensional space
of all such functions. Let diff(Rn) denote the infinite-dimensional Lie group
of diffeomorphism
s Rn → Rn, and diff(R) the infinite-dimensional Lie group of diffeomorphisms R → R. The product group
diff(Rn) × diff(R) acts
on Ω(Rn,R) in the following way: let φ : Rn → Rn and ψ : R → R be diffeormorphisms and f : Rn → R any smooth function. We define the group action as follows: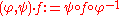
The orbit of f, denoted orb(f), of this group action is given by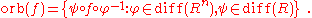
The members of a given orbit of this action have the following fact in common: we can find a diffeomorphic change of coordinate in Rn and a diffeomorphic change of coordinate in R such that one member of the orbit is carried to any other. A function f is said to have a type Ak-singularity if it lies in the orbit of
where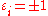
and k ≥ 0 is an integer.
By a normal form we mean a particularly simple representative of any given orbit. The above expressions for f give normal forms for the type Ak-singularities. The type Ak-singularities are special because they are amongst the simple singularities, this means that there are only a finite number of other orbits in a sufficiently small neighbourhood of the orbit of f.
This idea extends over the complex number
s where the normal forms are much simpler; for example: there is no need to distinguish εi = +1 from εi = −1.
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
an Ak, where k ≥ 0 is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, describes a level of degeneracy of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. The notation was introduced by V. I. Arnold.
Let f : Rn → R be a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. We denote by Ω(Rn,R) the infinite-dimensional space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
of all such functions. Let diff(Rn) denote the infinite-dimensional Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s Rn → Rn, and diff(R) the infinite-dimensional Lie group of diffeomorphisms R → R. The product group
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
diff(Rn) × diff(R) acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on Ω(Rn,R) in the following way: let φ : Rn → Rn and ψ : R → R be diffeormorphisms and f : Rn → R any smooth function. We define the group action as follows:
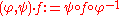
The orbit of f, denoted orb(f), of this group action is given by
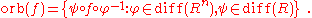
The members of a given orbit of this action have the following fact in common: we can find a diffeomorphic change of coordinate in Rn and a diffeomorphic change of coordinate in R such that one member of the orbit is carried to any other. A function f is said to have a type Ak-singularity if it lies in the orbit of
where
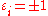and k ≥ 0 is an integer.By a normal form we mean a particularly simple representative of any given orbit. The above expressions for f give normal forms for the type Ak-singularities. The type Ak-singularities are special because they are amongst the simple singularities, this means that there are only a finite number of other orbits in a sufficiently small neighbourhood of the orbit of f.
This idea extends over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s where the normal forms are much simpler; for example: there is no need to distinguish εi = +1 from εi = −1.