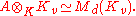Albert–Brauer–Hasse–Noether theorem
Encyclopedia
In algebraic number theory
, the Albert–Brauer–Hasse–Noether theorem states that a central simple algebra
over an algebraic number field
K which splits over every completion
Kv is a matrix algebra
over K. The theorem is an example of a local – global principle in algebraic number theory and
leads to a complete description of finite-dimensional division algebras over algebraic number fields in terms of their local invariants. It was proved independently by Helmut Hasse
, Richard Brauer
, and Emmy Noether
and by Abraham Adrian Albert
and Hasse.
of rank d over an algebraic number field
K. Suppose that for any valuation v, A splits over the corresponding local field Kv:
Then A is isomorphic to the matrix algebra Md(K).
, one shows that two central simple algebras A and B over an algebraic number field K are isomorphic over K if and only if their completions Av and Bv are isomorphic over the completion Kv for every v.
Together with the Grunwald–Wang theorem, the Albert–Brauer–Hasse–Noether theorem implies that every central simple algebra over an algebraic number field is cyclic, i.e. can be obtained by an explicit construction from a cyclic field extension L/K .
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, the Albert–Brauer–Hasse–Noether theorem states that a central simple algebra
Central simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
over an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
K which splits over every completion
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
Kv is a matrix algebra
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
over K. The theorem is an example of a local – global principle in algebraic number theory and
leads to a complete description of finite-dimensional division algebras over algebraic number fields in terms of their local invariants. It was proved independently by Helmut Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
, Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
, and Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
and by Abraham Adrian Albert
Abraham Adrian Albert
Abraham Adrian Albert was an American mathematician. In 1939, he received the first American Mathematical Society's Cole Prize in Algebra for his work on Riemann matrices...
and Hasse.
Statement of the theorem
Let A be a central simple algebraCentral simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
of rank d over an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
K. Suppose that for any valuation v, A splits over the corresponding local field Kv:
Then A is isomorphic to the matrix algebra Md(K).
Applications
Using the theory of Brauer groupBrauer group
In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
, one shows that two central simple algebras A and B over an algebraic number field K are isomorphic over K if and only if their completions Av and Bv are isomorphic over the completion Kv for every v.
Together with the Grunwald–Wang theorem, the Albert–Brauer–Hasse–Noether theorem implies that every central simple algebra over an algebraic number field is cyclic, i.e. can be obtained by an explicit construction from a cyclic field extension L/K .