Alexander's Star is a puzzle

Puzzle

A puzzle is a problem or enigma that tests the ingenuity of the solver. In a basic puzzle, one is intended to put together pieces in a logical way in order to come up with the desired solution...

 similar to the Rubik's Cube

Rubik's Cube

Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...

, in the shape of a great dodecahedron.

History

Alexander's Star was invented by Adam Alexander, an American mathematician, in 1982. It was patented on 26 March 1985, with US patent number 4,506,891, and sold by the Ideal Toy Corporation.

Description

The puzzle has 30 moving pieces, which rotate in star-shaped groups of five around its outermost vertices. The purpose of the puzzle is to rearrange the moving pieces so that each star is surrounded by five faces of the same color, and opposite stars are surrounded by the same color. This is equivalent to solving just the edges of a six-color Megaminx

Megaminx

The Megaminx is a dodecahedron-shaped puzzle similar to the Rubik's Cube. It has a total of 50 movable pieces to rearrange, compared to the 20 movable pieces of the Rubik's cube.- History :...

.

Permutations

There are 30 edges, each of which can be flipped into two positions, giving a theoretical maximum of 30!×2³⁰ permutations. This value is not reached for the following reasons:

1. Only even permutations of edges are possible, reducing the possible edge arrangements to 30!/2.
2. The orientation of the last edge is determined by the orientation of the other edges, reducing the number of edge orientations to 2²⁹.
3. Since opposite sides of the solved puzzle are the same color, each edge piece has a duplicate. It would be impossible to swap all 15 pairs (an odd permutation), so a reducing factor of 2¹⁴ is applied.
4. The orientation of the puzzle does not matter (since there are no fixed face centers to serve as reference points), dividing the final total by 60. There are 60 possible positions and orientations of the first edge, but all of them are equivalent because of the lack of face centers.

This gives a total of 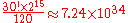possible combinations.

The precise figure is 72 431 714 252 715 638 411 621 302 272 000 000 (roughly 72.4 decillion on the short scale

Names of large numbers

This article lists and discusses the usage and derivation of names of large numbers, together with their possible extensions.The following table lists those names of large numbers which are found in many English dictionaries and thus have a special claim to being "real words"...

or 72.4 quintilliard on the long scale).

External links

• Description and solution