
Great dodecahedron
Encyclopedia
In geometry
, the great dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter-Dynkin diagram
of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), with five pentagons meeting at each vertex, intersecting each other making a pentagram
mic path.
.
If the great dodecahedron is considered as a properly intersected surface geometry, it has the same topology as a triakis icosahedron
with concave pyramids rather than convex ones.
A truncation
process applied to the great dodecahedron produces a series of nonconvex uniform polyhedra
. Truncating edges down to points produces the dodecadodecahedron as a rectified great dodecahedron. The process completes as a birectification, reducing the original faces down to points, and producing the small stellated dodecahedron.
The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 pentagon
al faces: 12 as the truncation facets of the former vertices, and 12 more (coinciding with the first set) as truncated pentagrams.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the great dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), with five pentagons meeting at each vertex, intersecting each other making a pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
mic path.
Images
| Transparent model | Spherical tiling |
|---|---|
 (With animation) |
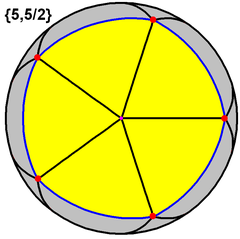 This polyhedron represents a spherical tiling with a density of 3. (One spherical pentagon face is shown above in yellow) |
| Net Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... |
Stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again... |
 Net for surface geometry |
 It can also be constructed as the second of three stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again... s of the dodecahedron, and referenced as Wenninger model [W21]. |
Related polyhedra
It shares the same edge arrangement as the convex regular icosahedronIcosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
.
If the great dodecahedron is considered as a properly intersected surface geometry, it has the same topology as a triakis icosahedron
Triakis icosahedron
In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron...
with concave pyramids rather than convex ones.
A truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
process applied to the great dodecahedron produces a series of nonconvex uniform polyhedra
Nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
. Truncating edges down to points produces the dodecadodecahedron as a rectified great dodecahedron. The process completes as a birectification, reducing the original faces down to points, and producing the small stellated dodecahedron.
The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
al faces: 12 as the truncation facets of the former vertices, and 12 more (coinciding with the first set) as truncated pentagrams.
| Name | Small stellated dodecahedron | Truncated small stellated dodecahedron | Dodecadodecahedron | Truncated great dodecahedron |
Great dodecahedron |
|---|---|---|---|---|---|
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||||
| Picture |  |
 |
 |
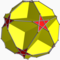 |
 |

