In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

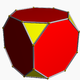
, a truncation is an operation in any dimension that cuts polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

 vertices, creating a new facet in place of each vertex.

Uniform truncation

In general any polyhedron (or polytope) can also be truncated with a degree of freedom how deep the cut is, as shown in Conway polyhedron notation

Conway polyhedron notation

Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...

 truncation operation.

A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron

Regular polyhedron

A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

 (or regular polytope

Regular polytope

In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...

) which creates a resulting uniform polyhedron

Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...

 (uniform polytope

Uniform polytope

A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....

) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra.

More abstractly any uniform polytope

Uniform polytope

A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....

 defined by a Coxeter-Dynkin diagram

Coxeter-Dynkin diagram

In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...

 with a single ring, can be also uniformly truncated, although it is not a geometric operation, but requires adjusted proportions to reach uniformity. For example Kepler's truncated icosidodecahedron

Truncated icosidodecahedron

In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....

 represents a uniform truncation of the icosidodecahedron

Icosidodecahedron

In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...

. It isn't a geometric truncation, which would produce rectangular faces, but a topological truncation that has been adjusted to fit the uniformity requirement.

Truncation of polygons

A truncated n-sided polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

 will have 2n sides (edges). A regular polygon uniformly truncated will become another regular polygon: t{n} is {2n}.

Star polygons can also be truncated. A truncated pentagram

Pentagram

A pentagram is the shape of a five-pointed star drawn with five straight strokes...

 {5/2} will look like a pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

, but is actually a double-covered (degenerate) decagon

Decagon

In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...

 with two sets of overlapping vertices and edges.

Truncation in regular polyhedra and tilings

When the term applies to truncating platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

s or regular tilings, usually "uniform truncation" is implied, which means to truncate until the original faces become regular polygons with double the sides.

This sequence shows an example of the truncation of a cube, using four steps of a continuous truncating process between a full cube

 and a rectified

Rectification (geometry)

In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...

 cube. The final polyhedron is a cuboctahedron

Cuboctahedron

In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...

.

The middle image is the uniform truncated cube

. It is represented by an extended Schläfli symbol t_0,1{p,q,...}.

Other truncations

In quasiregular polyhedra, a truncation is a more qualitative term where some other adjustments are made to adjust truncated faces to become regular. These are sometimes called rhombitruncations.

For example, the truncated cuboctahedron

Truncated cuboctahedron

In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...

 is not really a truncation since the cut vertices of the cuboctahedron

Cuboctahedron

In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...

 would form rectangular faces rather than squares, so a wider operation is needed to adjust the polyhedron to fit desired squares.

In the quasiregular duals, an alternate truncation operation only truncates alternate vertices. (This operation can also apply to any zonohedron

Zonohedron

A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...

 which have even-sided faces.)

The dual

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

 operation to truncation is the construction of a Kleetope

Kleetope

In geometry and polyhedral combinatorics, the Kleetope of a polyhedron or higher-dimensional convex polytope is another polyhedron or polytope formed by replacing each facet of with a shallow pyramid...

.

Uniform polyhedron and tiling examples

This table shows the truncation progression between the regular forms, with the rectified forms (full truncation) in the center. Comparable faces are colored red and yellow to show the continuum in the sequences.

Family	Original	Truncation	Rectification	Bitruncation (truncated dual)	Birecification (dual)
[3,3]	Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	Truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...	Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	Truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...	Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
[4,3]	Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...	Truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....	Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...	Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....	Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
[5,3]	Dodecahedron	Truncated dodecahedron Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :...	Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...	Truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....	Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
[6,3]	Hexagonal tiling	Truncated hexagonal tiling Truncated hexagonal tiling In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons and one triangle on each vertex....	Trihexagonal tiling Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex...	Hexagonal tiling	Triangular tiling
[7,3]	Order-3 heptagonal tiling	Order-3 truncated heptagonal tiling Order-3 truncated heptagonal tiling In geometry, the Truncated order-3 heptagonal tiling is a semiregular tiling of the hyperbolic plane. There is one triangle and two tetrakaidecagons on each vertex...	Triheptagonal tiling Triheptagonal tiling In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex...	Order-7 truncated triangular tiling Order-7 truncated triangular tiling In geometry, the Order 7 truncated heptagonal tiling, sometimes called the hyperbolic soccerball, is a semiregular tiling of the hyperbolic plane. There are two hexagons and one heptagon on each vertex, forming a pattern similar to a conventional soccer ball with heptagons in place of pentagons...	Order-7 triangular tiling
[8,3]	Order-3 Octagonal tiling	Order-3 truncated Octagonal tiling	Trioctagonal tiling	Order-8 truncated triangular tiling	Order-8 triangular tiling
[4,4]	Square tiling	Truncated square tiling Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon...	Square tiling	Truncated square tiling Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon...	Square tiling
[5,4]	pentagonal	truncated pentagonal	Rectified pentagonal	Truncated square	Square
[5,5]	Pentagonal	Truncated pentagonal	Rectified pentagonal	Truncated pentagonal	Pentagonal

Prismatic polyhedron examples

Family	Original	Truncation	Rectification (And dual)
[2,p]	Hexagonal hosohedron (As spherical tiling) {2,p}	Hexagonal prism Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... t{2,p}	Hexagonal dihedron Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... (As spherical tiling) {p,2}

rhombitruncated examples

These forms start with a rectified

Rectification (geometry)

In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...

 regular form which is truncated. The vertices are order-4, and a true geometric truncation would create rectangular faces. The uniform rhombitruction requires adjustment to create square faces.

Original	Rectification	Rhombitruncation
		Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
	Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...	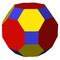Truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...
	Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...	Truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
	Trihexagonal tiling Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex...	Truncated trihexagonal tiling Great rhombitrihexagonal tiling In geometry, the truncated trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex... or great rhombitrihexagonal tiling
	Triheptagonal tiling Triheptagonal tiling In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex...	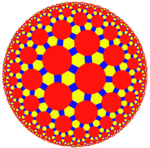Truncated triheptagonal tiling or great rhombitriheptagonal tiling
	Trioctagonal tiling	Truncated trioctagonal tiling or great rhombitrioctagonal tiling
	Square tiling	Truncated square tiling Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon...
	Tetrapentagonal tiling	Truncated tetrapentagonal tiling
	Order-4 pentagonal tiling	Order-4 truncated pentagonal tiling

Truncation in polychora and honeycomb tessellation

A regular polychoron or tessellation {p,q,r}, truncated becomes a uniform polychoron or tessellation with 2 cells: truncated {p,q}, and {q,r} cells are created on the truncated section.

See: uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

 and convex uniform honeycomb

Convex uniform honeycomb

In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...

.

Family [p,q,r]	Parent	Truncation	Rectification (birectified dual)	Bitruncation (bitruncated dual)
[3,3,3]	5-cell (self-dual)	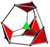truncated 5-cell Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...	rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10...	bitruncated 5-cell
[3,3,4]	16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....	truncated 16-cell	rectified 16-cell (Same as 24-cell)	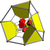bitruncated 16-cell (bitruncated tesseract)
[4,3,3]	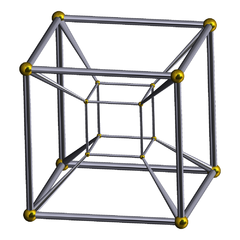Tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...	truncated tesseract Truncated tesseract In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell....	rectified tesseract Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra....	bitruncated tesseract (bitruncated 16-cell)
[3,4,3]	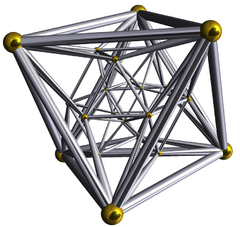24-cell (self-dual)	truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...	rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra....	bitruncated 24-cell
[3,3,5]	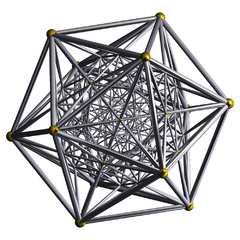600-cell	truncated 600-cell	rectified 600-cell Rectified 600-cell In geometry, a rectified 600-cell is a uniform polychoron formed as the rectification of the regular 600-cell.There are four rectifications of the 600-cell, including the zeroth, the 600-cell itself...	bitruncated 600-cell (bitruncated 120-cell)
[5,3,3]	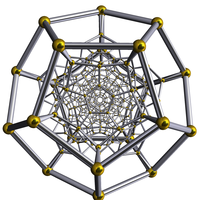120-cell	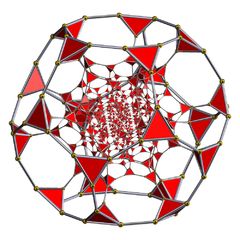truncated 120-cell Truncated 120-cell In geometry, a truncated 120-cell is a uniform polychoron formed as the truncation of the regular 120-cell.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 600-cell....	rectified 120-cell Rectified 120-cell In geometry, a rectified 120-cell is a uniform polychoron formed as the rectification of the regular 120-cell.There are four rectifications of the 120-cell, including the zeroth, the 120-cell itself...
[4,3,4]	cubic Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....  (self-dual)	truncated cubic Truncated cubic honeycomb The truncated cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of truncated cubes and octahedra in a ratio of 1:1.- Symmetry :...	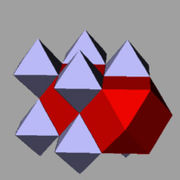rectified cubic Rectified cubic honeycomb The rectified cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of octahedra and cuboctahedra in a ratio of 1:1.- Symmetry :...	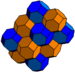bitruncated cubic Bitruncated cubic honeycomb The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra.It is one of 28 uniform honeycombs. It has 4 truncated octahedra around each vertex....
[3,5,3]	icosahedral (self-dual)	(No image) truncated icosahedral	(No image) rectified icosahedral	(No image) bitruncated icosahedral
[4,3,5]	cubic	(No image) truncated cubic	(No image) rectified cubic	(No image) bitruncated cubic (bitruncated dodecahedral)
[5,3,4]	dodecahedral	(No image) truncated dodecahedral	(No image) rectified dodecahedral
[5,3,5]	(No image) dodecahedral (self-dual)	(No image) truncated dodecahedral	(No image) rectified dodecahedral	(No image) bitruncated dodecahedral

See also

• uniform polyhedron
  Uniform polyhedron
  A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
  
  
• uniform polychoron
  Uniform polychoron
  In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
  
  
• Bitruncation (geometry)
• Rectification (geometry)
  Rectification (geometry)
  In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
  
  
• Alternation (geometry)
• Conway polyhedron notation
  Conway polyhedron notation
  Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...
  
  

External links

• Polyhedra Names, truncation