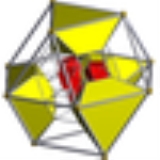
Rectified 24-cell
Encyclopedia
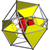 Schlegel diagram 8 of 24 cuboctahedral cells shown |
||
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
|
| Schläfli symbol | t1{3,4,3} t0,2{3,3,4} t0,2,3{31,1,1} |
|
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
||
| Cells | 48 | 24 3.4.3.4 Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...  24 4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...  |
| Faces | 240 | 96 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 144 {4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... |
| Edges | 288 | |
| Vertices | 96 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
  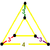 Triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
|
| Symmetry groups Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
F4 [3,4,3] B4 [3,3,4] D4 [31,1,1] |
|
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... , edge-transitive |
|
| Uniform index | 22 23 24 Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
|
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the rectified 24-cell is a uniform 4-dimensional polytope (or uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
), which is bounded by 48 cells: 24 cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s, and 24 cuboctahedra
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.
It can also be considered a cantellated 16-cell with the lower symmetries B4 = [3,3,4]. B4 would lead to a bicoloring of the cuboctahedral
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
cells into 8 and 16 each. It is also called a runcicantellated demitesseract in a D4 symmetry, giving 3 colors of cells, 8 for each.
Cartesian coordinates
A rectified 24-cell having an edge length of √2 has vertices given by all permutations and sign permutations of the following Cartesian coordinates:- (0,1,1,2) [4!/2!x23 = 96 vertices]
The dual configuration has all coordinate and sign permutations of:
- (0,2,2,2) [4x23 = 32 vertices]
- (1,1,1,3) [4x24 = 64 vertices]
Images
| Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... |
|
|---|---|
 |
|
| Center of stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... with 96 triangular faces blue |
|
Symmetry constructions
There are three different symmetry constructions of this polytope. The lowest construction can be doubled into
construction can be doubled into  by adding a mirror that maps the bifurcating nodes onto each other.
by adding a mirror that maps the bifurcating nodes onto each other.  can be mapped up to
can be mapped up to  symmetry by adding two mirror that map all three end nodes together.
symmetry by adding two mirror that map all three end nodes together.The vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is a triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
, containing two cubes and three cuboctahedra. The three symmetries can be seen with 3 colored cuboctahedra in the lowest
 construction, and two colors (1:2 ratio) in
construction, and two colors (1:2 ratio) in  , and all identical cuboctahedra in
, and all identical cuboctahedra in  .
.In
 symmetry one further symmetry exists that maps the two cubes in the vertex figure onto each other, represented by Coxeter symmetry notation
symmetry one further symmetry exists that maps the two cubes in the vertex figure onto each other, represented by Coxeter symmetry notation | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Order | Full symmetry group |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Facets | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|---|---|---|---|---|---|
 = [3,4,3] = [3,4,3] |
1152 (2304) |
3: 2: |
 |
||
 = [4,3,3] = [4,3,3] |
384 | [4,3,3] | 2,2: 2: |
 |
|
 = [3,31,1] = [3,31,1] |
192 | <[3,31,1]> = [4,3,3] [3[31,1,1]] = [3,4,3] |
1,1,1: 2: |
 |
Alternate names
- Rectified 24-cell (Norman Johnson)
- Cantellated 16-cell (Norman Johnson)
- Rectified icositetrachoron (Acronym rico) (George OlshevskyGeorge OlshevskyGeorge Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
, Jonathan Bowers)- Cantellated hexadecachoron
- Rectified polyoctahedron
- Disicositetrachoron
- Amboicositetrachoron (Neil Sloane & John Horton ConwayJohn Horton ConwayJohn Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
)

