Schlegel diagram
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Schlegel diagram is a projection of a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
from
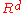into 
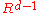through a point beyond one of its facets. The resulting entity is a polytopal subdivision of the facet in 
that is combinatorially equivalent to the original polytope. At the beginning of the 20th century, Schlegel diagrams were an important tool for studying combinatorial and topological properties of polytopes. In dimensions 3 and 4, a Schlegel diagram is a projection of a polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
into a plane figure and a projection of a polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
to 3-space, respectively. As such, Schlegel diagrams are commonly used as a means of visualizing four-dimensional polytopes.
Construction
A Schlegel diagram can be constructed by a perspective projection viewed from a point outside of the polytope, above the center of a facetFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
. All vertices and edges of the polytope are projected onto a hyperplane of that facet. If the polytope is convex, a point near the facet will exist which maps the facet outside, and all other facets inside, so no edges need to cross in the projection.
Examples
| Dodecahedron | Dodecaplex |
|---|---|
 12 pentagon faces in the plane |
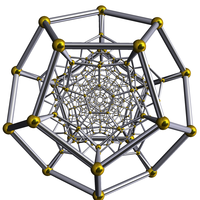 120 dodecahedral cells in 3-space |
See also
- Net (polyhedron)Net (polyhedron)In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron...
- A different approach for visualization by lowering the dimension of a polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
is to build a net, disconnecting facetFacetFacets are flat faces on geometric shapes. The organization of naturally occurring facets was key to early developments in crystallography, since they reflect the underlying symmetry of the crystal structure...
s, and unfolding until the facets can exist on a single hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
. This maintains the geometric scale and shape, but makes the topological connections harder to see.