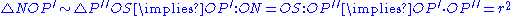Stereographic projection - AbsoluteAstronomy.com

The stereographic projection, in geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, is a particular mapping (function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

) that projects a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

onto a plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

and bijective

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

. It is conformal

Conformal map

In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...

, meaning that it preserves angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

s. It is neither isometric

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

nor area-preserving: that is, it preserves neither distances nor the areas of figures.

Intuitively, then, the stereographic projection is a way of picturing the sphere as the plane, with some inevitable compromises. Because the sphere and the plane appear in many areas of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

and its applications, so does the stereographic projection; it finds use in diverse fields including complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, cartography

Cartography

Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...

, geology

Geology

Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...

, and photography

Photography

Photography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film...

. In practice, the projection is carried out by computer

Computer

A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...

or by hand using a special kind of graph paper

Graph paper

Graph paper, graphing paper, grid paper or millimeter paper is writing paper that is printed with fine lines making up a regular grid. The lines are often used as guides for plotting mathematical functions or experimental data and drawing diagrams. It is commonly found in mathematics and...

called a stereonet or Wulff net.

History

The stereographic projection was known to Hipparchus

Hipparchus

Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...

, Ptolemy

Ptolemy

Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...

and probably earlier to the Egyptians

Ancient Egypt

Ancient Egypt was an ancient civilization of Northeastern Africa, concentrated along the lower reaches of the Nile River in what is now the modern country of Egypt. Egyptian civilization coalesced around 3150 BC with the political unification of Upper and Lower Egypt under the first pharaoh...

. It was originally known as the planisphere projection. Planisphaerium
Planisphaerium
The Planisphaerium is a work by Ptolemy. The title can be translated as "celestial plane" or "star chart". In this work Ptolemy explored the mathematics of mapping figures inscribed in the celestial sphere onto a plane by what is now known as stereographic projection...

by Ptolemy is the oldest surviving document that describes it. One of its most important uses was the representation of celestial charts. The term planisphere
Planisphere
A planisphere is a star chart analog computing instrument in the form of two adjustable disks that rotate on a common pivot. It can be adjusted to display the visible stars for any time and date. It is an instrument to assist in learning how to recognize stars and constellations...

is still used to refer to such charts.

It is believed that the earliest existing world map created by Gualterious Lud of St Dié, Lorraine, in 1507 is based upon the stereographic projection, mapping each hemisphere as a circular disk. The equator

Equator

An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....

ial aspect of the stereographic projection, commonly used for maps of the Eastern

Eastern Hemisphere

The Eastern Hemisphere, also Eastern hemisphere or eastern hemisphere, is a geographical term for the half of the Earth that is east of the Prime Meridian and west of 180° longitude. It is also used to refer to Europe, Asia, Africa, and Australasia, vis-à-vis the Western Hemisphere, which includes...

and Western Hemisphere

Western Hemisphere

The Western Hemisphere or western hemisphere is mainly used as a geographical term for the half of the Earth that lies west of the Prime Meridian and east of the Antimeridian , the other half being called the Eastern Hemisphere.In this sense, the western hemisphere consists of the western portions...

s in the 17th and 18th centuries (and 16th century - Jean Roze 1542; Rumold Mercator 1595), was utilised by the ancient astronomers like Ptolemy

Ptolemy

François d'Aiguillon

François d'Aguilon

François d'Aguilon , was a Belgian Jesuit mathematician, physicist and architect....

gave the stereographic projection its current name in his 1613 work Opticorum libri sex philosophis juxta ac mathematicis utiles (Six Books of Optics, useful for philosophers and mathematicians alike).

Definition

This section focuses on the projection of the unit sphere from the north pole onto the plane through the equator. Other formulations are treated in later sections.

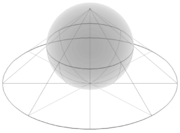
The unit sphere

Unit sphere

In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...

in three-dimensional space R³ is the set of points (x, y, z) such that x² + y² + z² = 1. Let N = (0, 0, 1) be the "north pole", and let M be the rest of the sphere. The plane z = 0 runs through the center of the sphere; the "equator" is the intersection of the sphere with this plane.

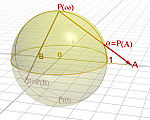
For any point P on M, there is a unique line through N and P, and this line intersects the plane z = 0 in exactly one point P'. Define the stereographic projection of P to be this point P' in the plane.

In Cartesian coordinates (x, y, z) on the sphere and (X, Y) on the plane, the projection and its inverse are given by the formulas

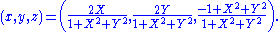
In spherical coordinates (φ, θ) on the sphere (with φ the zenith angle

Zenith Angle

Zenith Angle can refer to:* In astronomy, the angle made between the surface of the Earth and a line between the observer and the observed * The Zenith Angle is a science fiction novel authored by Bruce Sterling...

, 0 ≤ φ ≤ π, and θ the azimuth, 0 ≤ θ ≤ 2 π) and polar coordinates (R, Θ) on the plane, the projection and its inverse are

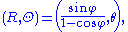
Here, φ is understood to have value π when R = 0. Also, there are many ways to rewrite these formulas using trigonometric identities. In cylindrical coordinates (r, θ, z) on the sphere and polar coordinates (R, Θ) on the plane, the projection and its inverse are

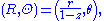
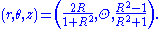
Properties

The stereographic projection defined in the preceding section sends the "south pole" (0, 0, −1) to (0, 0), the equator to the unit circle

Unit circle

In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...

, the southern hemisphere to the region inside the circle, and the northern hemisphere to the region outside the circle.

The projection is not defined at the projection point N = (0, 0, 1). Small neighborhoods of this point are sent to subsets of the plane far away from (0, 0). The closer P is to (0, 0, 1), the more distant its image is from (0, 0) in the plane. For this reason it is common to speak of (0, 0, 1) as mapping to "infinity" in the plane, and of the sphere as completing the plane by adding a "point at infinity". This notion finds utility in projective geometry

Projective geometry

In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...

and complex analysis. On a merely topological

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

level, it illustrates how the sphere is homeomorphic

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

to the one point compactification of the plane.

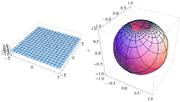
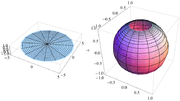
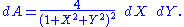
Stereographic projection is conformal, meaning that it preserves the angles at which curves cross each other (see figures). On the other hand, stereographic projection does not preserve area; in general, the area of a region of the sphere does not equal the area of its projection onto the plane. The area element is given in (X, Y) coordinates by

Along the unit circle, where X² + Y² = 1, there is no infinitesimal distortion of area. Near (0, 0) areas are distorted by a factor of 4, and near infinity areas are distorted by arbitrarily small factors.

The metric is given in (X, Y) coordinates by

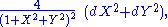
and is the unique formula found in Bernhard Riemann

Bernhard Riemann

Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....

's Habilitationsschrift on the foundations of geometry, delivered at Göttingen in 1854, and entitled Über die Hypothesen welche der Geometrie zu Grunde liegen.

No map from the sphere to the plane can be both conformal and area-preserving. If it were, then it would be a local isometry

Isometry

and would preserve Gaussian curvature

Gaussian curvature

In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...

. The sphere and the plane have different Gaussian curvatures, so this is impossible.

The conformality of the stereographic projection implies a number of convenient geometric properties. Circles on the sphere that do not pass through the point of projection are projected to circles on the plane. Circles on the sphere that do pass through the point of projection are projected to straight lines on the plane. These lines are sometimes thought of as circles through the point at infinity, or circles of infinite radius.

All lines in the plane, when transformed to circles on the sphere by the inverse of stereographic projection, intersect each other at infinity. Parallel lines, which do not intersect in the plane, are tangent at infinity. Thus all lines in the plane intersect somewhere in the sphere — either transversally at two points, or tangently at infinity. (Similar remarks hold about the real projective plane

Real projective plane

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...

, but the intersection relationships are different there.)

The loxodromes of the sphere map to curves on the plane of the form

where the parameter a measures the "tightness" of the loxodrome. Thus loxodromes correspond to logarithmic spiral

Logarithmic spiral

A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...

s. These spirals intersect radial lines in the plane at equal angles, just as the loxodromes intersect meridians on the sphere at equal angles.
The stereographic projection relates to the plane inversion in a simple way. Let P and Q be two points on the sphere with projections P' and Q' on the plane. Then P' and Q' are inversive images of each other in the image of the equatorial circle if and only if P and Q are reflections of each other in the equatorial plane.

In other words, if:

P is a point on the sphere, but not a 'north pole' N and not its antipode
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....

, the 'south pole' S,
P' is the image of P in a stereographic projection with the projection point N and
P" is the image of P in a stereographic projection with the projection point S,

then P' and P" are inversive images of each other in the unit circle.

Wulff net

Stereographic projection plots can be carried out by a computer using the explicit formulas given above. However, for graphing by hand these formulas are unwieldy; instead, it is common to use graph paper designed specifically for the task. To make this graph paper, one places a grid of parallels

Circle of latitude

A circle of latitude, on the Earth, is an imaginary east-west circle connecting all locations that share a given latitude...

and meridians on the hemisphere, and then stereographically projects these curves to the disk. The result is called a stereonet or Wulff net (named for the Russian mineralogist

Mineralogy

Mineralogy is the study of chemistry, crystal structure, and physical properties of minerals. Specific studies within mineralogy include the processes of mineral origin and formation, classification of minerals, their geographical distribution, as well as their utilization.-History:Early writing...

George (Yuri Viktorovich) Wulff ).

In the figure, the area-distorting property of the stereographic projection can be seen by comparing a grid sector near the center of the net with one at the far right of the net. The two sectors have equal areas on the sphere. On the disk, the latter has nearly four times the area as the former; if one uses finer and finer grids on the sphere, then the ratio of the areas approaches exactly 4.

The angle-preserving property of the projection can be seen by examining the grid lines. Parallels and meridians intersect at right angles on the sphere, and so do their images on the Wulff net.

For an example of the use of the Wulff net, imagine that we have two copies of it on thin paper, one atop the other, aligned and tacked at their mutual center. Suppose that we want to plot the point (0.321, 0.557, −0.766) on the lower unit hemisphere. This point lies on a line oriented 60° counterclockwise from the positive x-axis (or 30° clockwise from the positive y-axis) and 50° below the horizontal plane z = 0. Once these angles are known, there are four steps:

Using the grid lines, which are spaced 10° apart in the figures here, mark the point on the edge of the net that is 60° counterclockwise from the point (1, 0) (or 30° clockwise from the point (0, 1)).
Rotate the top net until this point is aligned with (1, 0) on the bottom net.
Using the grid lines on the bottom net, mark the point that is 50° toward the center from that point.
Rotate the top net oppositely to how it was oriented before, to bring it back into alignment with the bottom net. The point marked in step 3 is then the projection that we wanted.

To plot other points, whose angles are not such round numbers as 60° and 50°, one must visually interpolate between the nearest grid lines. It is helpful to have a net with finer spacing than 10°; spacings of 2° are common.

To find the central angle

Central angle

A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...

between two points on the sphere based on their stereographic plot, overlay the plot on a Wulff net and rotate the plot about the center until the two points lie on or near a meridian. Then measure the angle between them by counting grid lines along that meridian.

Other formulations and generalizations

Some authors define stereographic projection from the north pole (0, 0, 1) onto the plane z = −1, which is tangent to the unit sphere at the south pole (0, 0, −1). The values X and Y produced by this projection are exactly twice those produced by the equatorial projection described in the preceding section. For example, this projection sends the equator to the circle of radius 2 centered at the origin. While the equatorial projection produces no infinitesimal area distortion along the equator, this pole-tangent projection instead produces no infinitesimal area distortion at the south pole.

In general, one can define a stereographic projection from any point Q on the sphere onto any plane E such that

E is perpendicular to the diameter through Q, and
E does not contain Q.

As long as E meets these conditions, then for any point P other than Q the line through P and Q meets E in exactly one point P^′, which is defined to be the stereographic projection of P onto E.

All of the formulations of stereographic projection described thus far have the same essential properties. They are smooth bijections (diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

s) defined everywhere except at the projection point. They are conformal and not area-preserving.

More generally, stereographic projection may be applied to the n-sphere Sⁿ in (n + 1)-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

E^n + 1. If Q is a point of Sⁿ and E a hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

in E^n + 1, then the stereographic projection of a point P ∈ Sⁿ − {Q} is the point P^′ of intersection of the line

with E.

Still more generally, suppose that S is a (nonsingular) quadric hypersurface

Quadric

In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...

in the projective space

Projective space

In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....

P^n + 1. By definition, S is the locus of zeros of a non-singular quadratic form f(x₀, ..., x_n + 1) in the homogeneous coordinates

Homogeneous coordinates

In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...

x_i. Fix any point Q on S and a hyperplane E in P^n + 1 not containing Q. Then the stereographic projection of a point P in S − {Q} is the unique point of intersection of

with E. As before, the stereographic projection is conformal and invertible outside of a "small" set. The stereographic projection presents the quadric hypersurface as a rational hypersurface

Rational variety

In mathematics, a rational variety is an algebraic variety, over a given field K, which is birationally equivalent to projective space of some dimension over K...

. This construction plays a role in algebraic geometry

Algebraic geometry

Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...

and conformal geometry

Conformal geometry

In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...

Complex analysis

Although any stereographic projection misses one point on the sphere (the projection point), the entire sphere can be mapped using two projections from distinct projection points. In other words, the sphere can be covered by two stereographic parametrization

Parametrization

Parametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....

s (the inverses of the projections) from the plane. The parametrizations can be chosen to induce the same orientation

Orientation (mathematics)

In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...

on the sphere. Together, they describe the sphere as an oriented surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

(or two-dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

).

This construction has special significance in complex analysis. The point (X, Y) in the real plane can be identified with the complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

ζ = X + iY. The stereographic projection from the north pole onto the equatorial plane is then

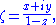
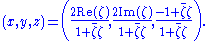
Similarly, letting ξ = X − iY be another complex coordinate, the functions

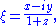
define a stereographic projection from the south pole onto the equatorial plane. The transition maps between the ζ- and ξ-coordinates are then ζ = 1 / ξ and ξ = 1 / ζ, with ζ approaching 0 as ξ goes to infinity, and vice versa. This facilitates an elegant and useful notion of infinity for the complex numbers and indeed an entire theory of meromorphic function

Meromorphic function

In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...

s mapping to the Riemann sphere

Riemann sphere

In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...

. The standard metric on the unit sphere agrees with the Fubini–Study metric on the Riemann sphere.

Visualization of lines and planes

The set of all lines through the origin in three-dimensional space forms a space called the real projective plane

Real projective plane

. This space is difficult to visualize, because it cannot be embedded

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

in three-dimensional space.

However, one can "almost" visualize it as a disk, as follows. Any line through the origin intersects the southern hemisphere z ≤ 0 in a point, which can then be stereographically projected to a point on a disk. Horizontal lines intersect the southern hemisphere in two antipodal point

Antipodal point

In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....

s along the equator, either of which can be projected to the disk; it is understood that antipodal points on the boundary of the disk represent a single line. (See quotient topology.) So any set of lines through the origin can be pictured, almost perfectly, as a set of points in a disk.

Also, every plane through the origin intersects the unit sphere in a great circle, called the trace of the plane. This circle maps to a circle under stereographic projection. So the projection lets us visualize planes as circular arcs in the disk. Prior to the availability of computers, stereographic projections with great circles often involved drawing large-radius arcs that required use of a beam compass. Computers now make this task much easier.

Further associated with each plane is a unique line, called the plane's pole, that passes through the origin and is perpendicular to the plane. This line can be plotted as a point on the disk just as any line through the origin can. So the stereographic projection also lets us visualize planes as points in the disk. For plots involving many planes, plotting their poles produces a less-cluttered picture than plotting their traces.

This construction is used to visualize directional data in crystallography and geology, as described below.

Other visualization

Stereographic projection is also applied to the visualization of polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

s. In a Schlegel diagram, an n-dimensional polytope in R^n + 1 is projected onto an n-dimensional sphere, which is then stereographically projected onto Rⁿ. The reduction from R^n + 1 to Rⁿ can make the polytope easier to visualize and understand.

Arithmetic geometry

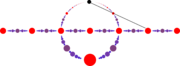
In elementary arithmetic geometry, stereographic projection from the unit circle provides a means to describe all primitive Pythagorean triple

Pythagorean triple

A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...

s. Specifically, stereographic projection from the north pole (0,1) onto the x-axis gives a one-to-one correspondence between the rational number

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

points (x,y) on the unit circle (with y ≠ 1) and the rational points of the x-axis. If (m/n, 0) is a rational point on the x-axis, then its inverse stereographic projection is the point

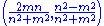
which gives Euclid's formula for a Pythagorean triple.

Weierstrass substitution

The pair of trigonometric functions can be thought of as parametrizing the unit circle. The stereographic projection gives an alternative parametrization of the unit circle: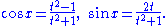

Under this reparametrization, the length element dx of the unit circle goes over to

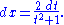
This substitution can sometimes simplify integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

s involving trigonometric functions.

Cartography

The fundamental problem of cartography is that no map from the sphere to the plane can accurately represent both angles (and thus shapes) and areas. In general, area-preserving map projection

Map projection

A map projection is any method of representing the surface of a sphere or other three-dimensional body on a plane. Map projections are necessary for creating maps. All map projections distort the surface in some fashion...

s are preferred for statistical

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

applications, because they behave well with respect to integration

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

, while angle-preserving (conformal) map projections are preferred for navigation

Navigation

Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...

.

Stereographic projection falls into the second category. When the projection is centered at the Earth's north or south pole, it has additional desirable properties: It sends meridian

Meridian (geography)

A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...

s to rays emanating from the origin and parallel

Circle of latitude

A circle of latitude, on the Earth, is an imaginary east-west circle connecting all locations that share a given latitude...

s to circles centered at the origin.

Crystallography

In crystallography

Crystallography

Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...

, the orientations of crystal

Crystal

A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...

axes and faces in three-dimensional space are a central geometric concern, for example in the interpretation of X-ray and electron diffraction

Electron diffraction

Electron diffraction refers to the wave nature of electrons. However, from a technical or practical point of view, it may be regarded as a technique used to study matter by firing electrons at a sample and observing the resulting interference pattern...

patterns. These orientations can be visualized as in the section Visualization of lines and planes above. That is, crystal axes and poles to crystal planes are intersected with the northern hemisphere and then plotted using stereographic projection. A plot of poles is called a pole figure.

In electron diffraction

Electron diffraction

, Kikuchi line

Kikuchi line

Kikuchi lines pair up to form bands in electron diffraction from single crystal specimens, there to serve as "roads in orientation-space" for microscopists not sure what they are looking at. In transmission electron microscopes, they are easily seen in diffraction from regions of the specimen thick...

pairs appear as bands decorating the intersection between lattice plane traces and the Ewald sphere thus providing experimental access to a crystal's stereographic projection. Model Kikuchi maps in reciprocal space, and fringe visibility maps for use with bend contours in direct space, thus act as road maps for exploring orientation space with crystals in the transmission electron microscope.

Geology

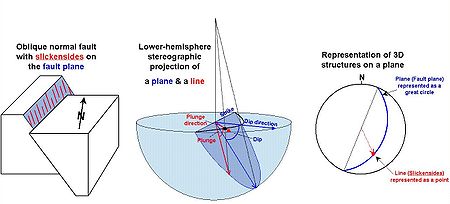
Researchers in structural geology

Structural geology

Structural geology is the study of the three-dimensional distribution of rock units with respect to their deformational histories. The primary goal of structural geology is to use measurements of present-day rock geometries to uncover information about the history of deformation in the rocks, and...

are concerned with the orientations of planes and lines for a number of reasons. The foliation

Foliation (geology)

Foliation is any penetrative planar fabric present in rocks. Foliation is common to rocks affected by regional metamorphic compression typical of orogenic belts. Rocks exhibiting foliation include the standard sequence formed by the prograde metamorphism of mudrocks; slate, phyllite, schist and...

of a rock is a planar feature that often contains a linear feature called lineation. Similarly, a fault plane is a planar feature that may contain linear features such as slickenside

Slickenside

s.

These orientations of lines and planes at various scales can be plotted using the methods of the Visualization of lines and planes section above. As in crystallography, planes are typically plotted by their poles. Unlike crystallography, the southern hemisphere is used instead of the northern one (because the geological features in question lie below the Earth's surface). In this context the stereographic projection is often referred to as the equal-angle lower-hemisphere projection. The equal-area lower-hemisphere projection defined by the Lambert azimuthal equal-area projection

Lambert azimuthal equal-area projection

The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk . It accurately represents area in all regions of the sphere, but it does not accurately represent angles...

is also used, especially when the plot is to be subjected to subsequent statistical analysis such as density contouring

Contour line

A contour line of a function of two variables is a curve along which the function has a constant value. In cartography, a contour line joins points of equal elevation above a given level, such as mean sea level...

Photography

Some fisheye lens

Fisheye lens

In photography, a fisheye lens is a wide-angle lens that takes in a broad, panoramic and hemispherical image. Originally developed for use in meteorology to study cloud formation and called "whole-sky lenses", fisheye lenses quickly became popular in general photography for their unique, distorted...

es use a stereographic projection to capture a wide angle view. Compared to more traditional fisheye lenses which use an equal-area projection, areas close to the edge retain their shape, and straight lines are less curved. However, stereographic fisheye lenses are typically more expensive to manufacture. Image remapping software, such as Panotools, allows the automatic remapping of photos from an equal-area fisheye to a stereographic projection.

The stereographic projection has been used to map spherical panoramas. This results in effects known as a little planet (when the center of projection is the nadir

Nadir

The nadir is the direction pointing directly below a particular location; that is, it is one of two vertical directions at a specified location, orthogonal to a horizontal flat surface there. Since the concept of being below is itself somewhat vague, scientists define the nadir in more rigorous...

) and a tube (when the center of projection is the zenith

Zenith

The zenith is an imaginary point directly "above" a particular location, on the imaginary celestial sphere. "Above" means in the vertical direction opposite to the apparent gravitational force at that location. The opposite direction, i.e...

).

The popularity of using stereographic projections to map panoramas over other azimuthal projections is attributed to the shape preservation that results from the conformality of the projection.

External links

Time Lapse Stereographic Projection
Planetmath.org
Table of examples and properties of all common projections, from radicalcartography.net
Three dimensional Java Applet
Stereographic Projection and Inversion from cut-the-knot
Cut-the-knot
Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
Examples of miniplanet panoramas, majority in UK
Examples of miniplanet panoramas, majority in Czech Republic
Examples of miniplanet panoramas, majority in Poland
DoITPoMS Teaching and Learning Package- "The Stereographic Projection"

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

History

Definition

Properties

Wulff net

Other formulations and generalizations

Complex analysis

Visualization of lines and planes

Other visualization

Arithmetic geometry

Weierstrass substitution

Cartography

Crystallography

Geology

Photography

See also

External links