Orientation (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the notion of orientation makes sense in arbitrary dimensions. In this setting, the orientation of an ordered basis is a kind of asymmetry that makes a reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
impossible to replicate by means of a simple rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
. Thus, in three dimensions, it is impossible to make the left hand of a human figure into the right hand of the figure by applying a rotation alone, but it is possible to do so by reflecting the figure in a mirror. As a result, in the three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the two possible basis orientations are called right-handed and left-handed (or right-chiral and left-chiral).
The orientation on a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is the arbitrary choice of which ordered bases are "positively" oriented and which are "negatively" oriented. In the three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, right-handed bases are typically declared to be positively oriented, but the choice is arbitrary, as they may also be assigned a negative orientation. A vector space with an orientation is called an oriented vector space, while one without a choice of orientation is called .
Definition
Let V be a finite-dimensional real vector space and let b1 and b2 be two ordered bases for V. It is a standard result in linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
that there exists a unique linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
A : V → V that takes b1 to b2. The bases b1 and b2 are said to have the same orientation (or be consistently oriented) if A has positive determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
; otherwise they have opposite orientations. The property of having the same orientation defines an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the set of all ordered bases for V. If V is non-zero, there are precisely two equivalence classes determined by this relation. An orientation on V is an assignment of +1 to one equivalence class and −1 to the other.
Every ordered basis lives in one equivalence class or another. Thus any choice of a privileged ordered basis for V determines an orientation: the orientation class of the privileged basis is declared to be positive. For example, the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
on Rn provides a standard orientation on Rn (in turn, the orientation of the standard basis depends on the orientation of the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
on which it is built). Any choice of a linear isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between V and Rn will then provide an orientation on V.
The ordering of elements in a basis is crucial. Two bases with a different ordering will differ by some permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
. They will have the same/opposite orientations according to whether the signature of this permutation is ±1. This is because the determinant of a permutation matrix
Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
is equal to the signature of the associated permutation.
Similarly, let A be a nonsingular linear mapping of vector space Rn to Rn. This mapping is orientation-preserving if its determinant is positive. For instance, in R3 a rotation around the Z Cartesian axis by an angle α is orientation-preserving:
-
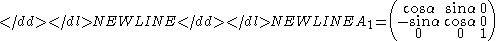
while a reflection by the XY Cartesian plane is not orientation-preserving:-
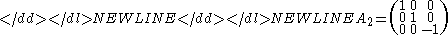
Zero-dimensional case
The concept of orientation defined above did not quite apply to zero-dimensional vector spaces (as the only empty matrix is the identity (with determinant 1), so there will be only one equivalence class). However, it is useful to be able to assign different orientations to a point (e.g. orienting the boundary of a 1-dimensional manifold). A more general definition of orientation that works regardless of dimension is the following: An orientation on V is a map from the set of ordered bases of V to the set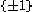
that is invariant under base changes with positive determinant and changes sign under base changes with negative determinant (it is equivarient with respect to the homomorphism 
). The set of ordered bases of the zero-dimensional vector space has one element (the empty set), and so there are two maps from this set to 
.
A subtle point is that a zero-dimensional vector space is naturally (canonically) oriented, so we can talk about an orientation being positive (agreeing with the canonical orientation) or negative (disagreeing). An application is interpreting the Fundamental theorem of calculusFundamental theorem of calculusThe first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
as a special case of Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
.
Two ways of seeing this are:- A zero-dimensional vector space is a point, and there is a unique map from a point to a point, so every zero-dimensional vector space is naturally identified with
, and thus is oriented. - The 0th exterior power of a vector space is the ground field
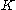, which here is 
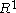, which has an orientation (given by the standard basis).
Multilinear algebra
For any n-dimensional real vector space V we can form the kth-exterior power of V, denoted ΛkV. This is a real vector space of dimension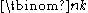
Binomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
. The vector space ΛnV (called the top exterior power) therefore has dimension 1. That is, ΛnV is just a real line. There is no a priori choice of which direction on this line is positive. An orientation is just such a choice. Any nonzero linear form ω on ΛnV determines an orientation of V by declaring that x is in the positive direction when ω(x) > 0. To connect with the basis point of view we say that the positively oriented bases are those on which ω evaluates to a positive number (since ω is an n-form we can evaluate it on an ordered set of n vectors, giving an element of R). The form ω is called an orientation form. If {ei} is a privileged basis for V and {ei*} is the dual basis, then the orientation form giving the standard orientation is e1*∧e2*∧…∧en*.
The connection of this with the determinant point of view is:
the determinant of an endomorphism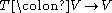
can be interpreted as the induced action on the top exterior power.
Lie group theory
Let B be the set of all ordered bases for V. Then the general linear groupGeneral linear groupIn mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(V) actsGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
freely and transitively on B. (In fancy language, B is a GL(V)-torsor). This means that as a manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, B is (noncanonically) homeomorphic to GL(V). Note that the group GL(V) is not connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, but rather has two connected componentConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
s according to whether the determinant of the transformation is positive or negative (except for GL0, which is the trivial group and thus has a single connected component; this corresponds to the canonical orientation on a zero-dimensional vector space). The identity componentIdentity componentIn mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of GL(V) is denoted GL+(V) and consists of those transformations with positive determinant. The action of GL+(V) on B is not transitive: there are two orbits which correspond to the connected components of B. These orbits are precisely the equivalence classes referred to above. Since B does not have a distinguished element (i.e. a privileged basis) there is no natural choice of which component is positive. Contrast this with GL(V) which does have a privileged component: the component of the identity. A specific choice of homeomorphism between B and GL(V) is equivalent to a choice of a privileged basis and therefore determines an orientation.
More formally: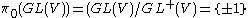
,
and the Stiefel manifoldStiefel manifoldIn mathematics, the Stiefel manifold Vk is the set of all orthonormal k-frames in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel...
of n-frames in
is a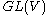 
-torsor, so 
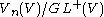is a torsor over 
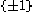, i.e., it's 2 points, and a choice of one of them is an orientation.
Geometric algebra
The various objects of geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
are charged with three attributes or features: attitude, orientation, and magnitude. For example, a vector has an attitude given by a straight line parallel to it, an orientation given by its sense (often indicated by an arrowhead) and a magnitude given by its length. Similarly, a bivectorBivectorIn mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
in three dimensions has an attitude given by the family of planes associated with it (possibly specified by the normal lineTangential and normal componentsIn mathematics, given a vector at a point on a curve, that vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the curve, called the normal component of the vector...
common to these planes ), an orientation (sometimes denoted by a curved arrow in the plane) indicating a choice of sense of traversal of its boundary (its circulation), and a magnitude given by the area of the parallelogram defined by its two vectors.
Orientation on manifolds
One can also discuss orientation on manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. Each point p on an n-dimensional differentiable manifold has a tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
TpM which is an n-dimensional real vector space. One can assign to each of these vector spaces an orientation. However, one would like to know whether it is possible to choose the orientations so that they "vary smoothly" from point to point. Due to certain topologicalTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
restrictions, there are situations when this is impossible. A manifold which admits a smooth choice of orientations for its tangents spaces is said to be orientable. See the article on orientabilityOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
for more on orientations of manifolds.
See also
- Sign conventionSign conventionIn physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
- Rotation representation (mathematics)Rotation representation (mathematics)In geometry a rotation representation expresses a rotation as a mathematical transformation. In physics, this concept extends to classical mechanics where rotational kinematics is the science of describing with numbers the purely rotational motion of an object.According to Euler's rotation theorem...
- Chirality (mathematics)Chirality (mathematics)In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
- Right-hand ruleRight-hand ruleIn mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
- Even and odd permutationsEven and odd permutationsIn mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
- Cartesian coordinate systemCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
- Attitude (geometry)
- PseudovectorPseudovectorIn physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
– Pseudovectors are a consequence of oriented spaces. - OrientabilityOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
– Discussion about the possibility of having orientations in a space.
- A zero-dimensional vector space is a point, and there is a unique map from a point to a point, so every zero-dimensional vector space is naturally identified with
-