Tangent space
Encyclopedia
In mathematics
, the tangent space of a manifold
facilitates the generalization of vectors from affine space
s to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other.
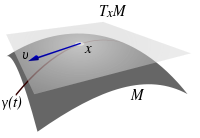
a tangent space, a real vector space
which intuitively contains the possible "directions" in which one can tangentially pass through x. The elements of the tangent space are called tangent vectors at x. This is a generalization of the notion of a bound vector in a Euclidean space
. All the tangent spaces have the same dimension, equal to the dimension of the manifold
.
For example, if the given manifold is a 2-sphere
, one can picture the tangent space at a point as the plane which touches the sphere at that point and is perpendicular
to the sphere's radius through the point. More generally, if a given manifold is thought of as an embedded
submanifold
of Euclidean space
one can picture the tangent space in this literal fashion.
In algebraic geometry
, in contrast, there is an intrinsic definition of tangent space at a point P of a variety
V, that gives a vector space of dimension at least that of V. The points P at which the dimension is exactly that of V are called the non-singular points; the others are singular points. For example, a curve that crosses itself doesn't have a unique tangent line at that point. The singular points of V are those where the 'test to be a manifold' fails. See Zariski tangent space
.
Once tangent spaces have been introduced, one can define vector field
s, which are abstractions of the velocity field of particles moving on a manifold. A vector field attaches to every point of the manifold a vector from the tangent space at that point, in a smooth manner. Such a vector field serves to define a generalized ordinary differential equation
on a manifold: a solution to such a differential equation is a differentiable curve
on the manifold whose derivative at any point is equal to the tangent vector attached to that point by the vector field.
All the tangent spaces can be "glued together" to form a new differentiable manifold of twice the dimension, the tangent bundle
of the manifold.
of M containing x. Suppose two curves γ1 : (-1,1) → M and γ2 : (-1,1) → M with γ1(0) = γ2(0) = x are given such that φ ∘ γ1 and φ ∘ γ2 are both differentiable at 0. Then γ1 and γ2 are called equivalent at 0 if the ordinary derivatives of φ ∘ γ1 and φ ∘ γ2 at 0 coincide. This defines an equivalence relation
on such curves, and the equivalence classes are known as the tangent vectors of M at x. The equivalence class of the curve γ is written as γ'(0). The tangent space of M at x, denoted by TxM, is defined as the set of all tangent vectors; it does not depend on the choice of chart φ.
To define the vector space operations on TxM, we use a chart φ : U → Rn and define the map
(dφ)x : TxM → Rn by (dφ)x(γ'(0)) =
(φ ∘ γ)(0). It turns out that this map is bijective and can thus be used to transfer the vector space operations from Rn over to TxM, turning the latter into an n-dimensional real vector space. Again, one needs to check that this construction does not depend on the particular chart φ chosen, and in fact it does not.
for the pointwise product
and sum of functions and scalar multiplication.
Pick a point x in M. A derivation
at x is a linear map D : C∞(M) → R which has the property that for all ƒ, g in C∞(M):
modeled on the product rule
of calculus. These derivations form a real vector space in a natural manner; this is the tangent space TxM.
The relation between the tangent vectors defined earlier and derivations is as follows: if γ is a curve with tangent vector γ'(0), then the corresponding derivation is D(ƒ) = (ƒ ∘ γ)'(0) (where the derivative is taken in the ordinary sense, since ƒ ∘ γ is a function from (-1,1) to R).
Generalizations of this definition are possible, for instance to complex manifold
s and algebraic varieties
. However, instead of examining derivations D from the full algebra of functions, one must instead work at the level of germs
of functions. The reason is that the structure sheaf may not be fine
for such structures. For instance, let X be an algebraic variety with structure sheaf OX. Then the Zariski tangent space
at a point p∈X is the collection of K-derivations D:OX,p→K, where K is the ground field
and OX,p is the stalk of OX at p.
, I, in C∞(M) consisting of all functions, ƒ, such that ƒ(x) = 0. Then I and I 2 are real vector spaces, and TxM may be defined as the dual space
of the quotient space
I / I 2. This latter quotient space is also known as the cotangent space
of M at x.
While this definition is the most abstract, it is also the one most easily transferred to other settings, for instance to the varieties
considered in algebraic geometry
.
If D is a derivation, then D(ƒ) = 0 for every ƒ in I2, and this means that D gives rise to a linear map I / I2 → R. Conversely, if r : I / I2 → R is a linear map, then D(ƒ) = r((ƒ - ƒ(x)) + I 2) is a derivation. This yields the correspondence between the tangent space defined via derivations and the tangent space defined via the cotangent space.
), and the tangent spaces are all naturally identified with Rn.
s. Given a vector v in Rn one defines the directional derivative of a smooth map ƒ: Rn→R at a point x by
This map is naturally a derivation. Moreover, it turns out that every derivation of C∞(Rn) is of this form. So there is a one-to-one map between vectors (thought of as tangent vectors at a point) and derivations.
Since tangent vectors to a general manifold can be defined as derivations it is natural to think of them as directional derivatives. Specifically, if v is a tangent vector of M at a point x (thought of as a derivation) then define the directional derivative in the direction v by
where ƒ: M → R is an element of C∞(M).
If we think of v as the direction of a curve, v = γ'(0), then we write
If the tangent space is defined via curves, the map is defined as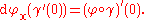
If instead the tangent space is defined via derivations, then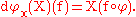
The linear map dφx is called variously the derivative, total derivative, differential, or pushforward of φ at x. It is frequently expressed using a variety of other notations: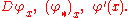
In a sense, the derivative is the best linear approximation to φ near x. Note that when N = R, the map dφx : TxM→R coincides with the usual notion of the differential
of the function φ. In local coordinates
the derivative of ƒ is given by the Jacobian.
An important result regarding the derivative map is the following:
This is a generalization of the inverse function theorem
to maps between manifolds.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the tangent space of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
facilitates the generalization of vectors from affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
s to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other.
Informal description
In differential geometry, one can attach to every point x of a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
a tangent space, a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
which intuitively contains the possible "directions" in which one can tangentially pass through x. The elements of the tangent space are called tangent vectors at x. This is a generalization of the notion of a bound vector in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. All the tangent spaces have the same dimension, equal to the dimension of the manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
For example, if the given manifold is a 2-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, one can picture the tangent space at a point as the plane which touches the sphere at that point and is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the sphere's radius through the point. More generally, if a given manifold is thought of as an embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
one can picture the tangent space in this literal fashion.
In algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, in contrast, there is an intrinsic definition of tangent space at a point P of a variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V, that gives a vector space of dimension at least that of V. The points P at which the dimension is exactly that of V are called the non-singular points; the others are singular points. For example, a curve that crosses itself doesn't have a unique tangent line at that point. The singular points of V are those where the 'test to be a manifold' fails. See Zariski tangent space
Zariski tangent space
In algebraic geometry, the Zariski tangent space is a construction that defines a tangent space at a point P on an algebraic variety V...
.
Once tangent spaces have been introduced, one can define vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s, which are abstractions of the velocity field of particles moving on a manifold. A vector field attaches to every point of the manifold a vector from the tangent space at that point, in a smooth manner. Such a vector field serves to define a generalized ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
on a manifold: a solution to such a differential equation is a differentiable curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
on the manifold whose derivative at any point is equal to the tangent vector attached to that point by the vector field.
All the tangent spaces can be "glued together" to form a new differentiable manifold of twice the dimension, the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of the manifold.
Formal definitions
There are various equivalent ways of defining the tangent spaces of a manifold. While the definition via velocities of curves is quite straightforward given the above intuition, it is also the most cumbersome to work with. More elegant and abstract approaches are described below.Definition as velocities of curves
Suppose M is a Ck manifold (k ≥ 1) and x is a point in M. Pick a chart φ : U → Rn where U is an open subsetOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of M containing x. Suppose two curves γ1 : (-1,1) → M and γ2 : (-1,1) → M with γ1(0) = γ2(0) = x are given such that φ ∘ γ1 and φ ∘ γ2 are both differentiable at 0. Then γ1 and γ2 are called equivalent at 0 if the ordinary derivatives of φ ∘ γ1 and φ ∘ γ2 at 0 coincide. This defines an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on such curves, and the equivalence classes are known as the tangent vectors of M at x. The equivalence class of the curve γ is written as γ'(0). The tangent space of M at x, denoted by TxM, is defined as the set of all tangent vectors; it does not depend on the choice of chart φ.
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
(dφ)x : TxM → Rn by (dφ)x(γ'(0)) =
(φ ∘ γ)(0). It turns out that this map is bijective and can thus be used to transfer the vector space operations from Rn over to TxM, turning the latter into an n-dimensional real vector space. Again, one needs to check that this construction does not depend on the particular chart φ chosen, and in fact it does not.Definition via derivations
Suppose M is a C∞ manifold. A real-valued function ƒ: M → R belongs to C∞(M) if ƒ ∘ φ−1 is infinitely often differentiable for every chart φ : U → Rn. C∞(M) is a real associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
for the pointwise product
Pointwise product
The pointwise product of two functions is another function, obtained by multiplying the image of the two functions at each value in the domain...
and sum of functions and scalar multiplication.
Pick a point x in M. A derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
at x is a linear map D : C∞(M) → R which has the property that for all ƒ, g in C∞(M):
modeled on the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
of calculus. These derivations form a real vector space in a natural manner; this is the tangent space TxM.
The relation between the tangent vectors defined earlier and derivations is as follows: if γ is a curve with tangent vector γ'(0), then the corresponding derivation is D(ƒ) = (ƒ ∘ γ)'(0) (where the derivative is taken in the ordinary sense, since ƒ ∘ γ is a function from (-1,1) to R).
Generalizations of this definition are possible, for instance to complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s and algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. However, instead of examining derivations D from the full algebra of functions, one must instead work at the level of germs
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of functions. The reason is that the structure sheaf may not be fine
Injective sheaf
In mathematics, injective sheaves of abelian groups are used to construct the resolutions needed to define sheaf cohomology ....
for such structures. For instance, let X be an algebraic variety with structure sheaf OX. Then the Zariski tangent space
Zariski tangent space
In algebraic geometry, the Zariski tangent space is a construction that defines a tangent space at a point P on an algebraic variety V...
at a point p∈X is the collection of K-derivations D:OX,p→K, where K is the ground field
Ground field
In mathematics, a ground field is a field K fixed at the beginning of the discussion. It is used in various areas of algebra: for example in linear algebra where the concept of a vector space may be developed over any field; and in algebraic geometry, where in the foundational developments of André...
and OX,p is the stalk of OX at p.
Definition via the cotangent space
Again we start with a C∞ manifold, M, and a point, x, in M. Consider the idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, I, in C∞(M) consisting of all functions, ƒ, such that ƒ(x) = 0. Then I and I 2 are real vector spaces, and TxM may be defined as the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
I / I 2. This latter quotient space is also known as the cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
of M at x.
While this definition is the most abstract, it is also the one most easily transferred to other settings, for instance to the varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
considered in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
If D is a derivation, then D(ƒ) = 0 for every ƒ in I2, and this means that D gives rise to a linear map I / I2 → R. Conversely, if r : I / I2 → R is a linear map, then D(ƒ) = r((ƒ - ƒ(x)) + I 2) is a derivation. This yields the correspondence between the tangent space defined via derivations and the tangent space defined via the cotangent space.
Properties
If M is an open subset of Rn, then M is a C∞ manifold in a natural manner (take the charts to be the identity mapsIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
), and the tangent spaces are all naturally identified with Rn.
Tangent vectors as directional derivatives
Another way to think about tangent vectors is as directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
s. Given a vector v in Rn one defines the directional derivative of a smooth map ƒ: Rn→R at a point x by
This map is naturally a derivation. Moreover, it turns out that every derivation of C∞(Rn) is of this form. So there is a one-to-one map between vectors (thought of as tangent vectors at a point) and derivations.
Since tangent vectors to a general manifold can be defined as derivations it is natural to think of them as directional derivatives. Specifically, if v is a tangent vector of M at a point x (thought of as a derivation) then define the directional derivative in the direction v by
where ƒ: M → R is an element of C∞(M).
If we think of v as the direction of a curve, v = γ'(0), then we write
The derivative of a map
Every smooth (or differentiable) map φ : M → N between smooth (or differentiable) manifolds induces natural linear maps between the corresponding tangent spaces:If the tangent space is defined via curves, the map is defined as
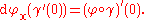
If instead the tangent space is defined via derivations, then
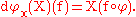
The linear map dφx is called variously the derivative, total derivative, differential, or pushforward of φ at x. It is frequently expressed using a variety of other notations:
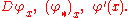
In a sense, the derivative is the best linear approximation to φ near x. Note that when N = R, the map dφx : TxM→R coincides with the usual notion of the differential
Differential (calculus)
In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
of the function φ. In local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
the derivative of ƒ is given by the Jacobian.
An important result regarding the derivative map is the following:
- Theorem. If φ : M → N is a local diffeomorphismLocal diffeomorphismIn mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
at x in M then dφx : TxM → Tφ(x)N is a linear isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. Conversely, if dφx is an isomorphism then there is an open neighborhoodOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
U of x such that φ maps U diffeomorphically onto its image.
This is a generalization of the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
to maps between manifolds.
External links
- Tangent Planes at MathWorld