Cotangent space
Encyclopedia
In differential geometry, one can attach to every point x of a smooth (or differentiable) manifold a vector space
called the cotangent space at x. Typically, the cotangent space is defined as the dual space
of the tangent space
at x, although there are more direct definitions (see below). The elements of the cotangent space are called cotangent vectors or tangent covectors.
of the manifold.
The tangent space and the cotangent space at a point are both real vector spaces of the same dimension and therefore isomorphic to each other via many possible isomorphisms. The introduction of a Riemannian metric or a symplectic form gives rise to a natural isomorphism between the tangent space and the cotangent space at a point, associating to any tangent covector a canonical tangent vector.
at x. Then the cotangent space at x is defined as the dual space
of TxM:
Concretely, elements of the cotangent space are linear functional
s on TxM. That is, every element α ∈ Tx*M is a linear map
where F is the underlying field
of the vector space being considered. In most cases, this is the field of real number
s. The elements of Tx*M are called cotangent vectors.
Let M be a smooth manifold and let x be a point in M. Let Ix be the ideal
of all functions in C∞(M) vanishing at x, and let Ix2 be the set of functions of the form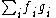
, where fi, gi ∈ Ix. Then Ix and Ix2 are real vector spaces and the cotangent space is defined as the quotient space
Tx*M = Ix / Ix2.
This formulation is analogous to the construction of the cotangent space to define the Zariski tangent space
in algebraic geometry. The construction also generalizes to locally ringed spaces.
. The differential of f at a point x is the map
where Xx is a tangent vector
at x, thought of as a derivation. That is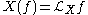
is the Lie derivative
of f in the direction X, and one has df(X)=X(f). Equivalently, we can think of tangent vectors as tangents to curves, and write
In either case, dfx is a linear map on TxM and hence it is a tangent covector at x.
We can then define the differential map d : C∞(M) → Tx*M at a point x as the map which sends f to dfx. Properties of the differential map include:
The differential map provides the link between the two alternate definitions of the cotangent bundle given above. Given a function f ∈ Ix (a smooth function vanishing at x) we can form the linear functional dfx as above. Since the map d restricts to 0 on Ix2 (the reader should verify this), d descends to a map from Ix / Ix2 to the dual of the tangent space, (TxM)*. One can show that this map is an isomorphism, establishing the equivalence of the two definitions.
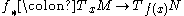
every such map induces a linear map (called the pullback) between the cotangent spaces, only this time in the reverse direction: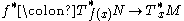
The pullback is naturally defined as the dual (or transpose) of the pushforward. Unraveling the definition, this means the following: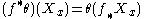
where θ ∈ Tf(x)*N and Xx ∈ TxM. Note carefully where everything lives.
If we define tangent covectors in terms of equivalence classes of smooth maps vanishing at a point then the definition of the pullback is even more straightforward. Let g be a smooth function on N vanishing at f(x). Then the pullback of the covector determined by g (denoted dg) is given by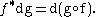
That is, it is the equivalence class of functions on M vanishing at x determined by g o f.
, are called differential k-forms
. They can be thought of as alternating, multilinear maps on k tangent vectors.
For this reason, tangent covectors are frequently called one-form
s.
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
called the cotangent space at x. Typically, the cotangent space is defined as the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at x, although there are more direct definitions (see below). The elements of the cotangent space are called cotangent vectors or tangent covectors.
Properties
All cotangent spaces on a connected manifold have the same dimension, equal to the dimension of the manifold. All the cotangent spaces of a manifold can be "glued together" (i.e. unioned and endowed with a topology) to form a new differentiable manifold of twice the dimension, the cotangent bundleCotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of the manifold.
The tangent space and the cotangent space at a point are both real vector spaces of the same dimension and therefore isomorphic to each other via many possible isomorphisms. The introduction of a Riemannian metric or a symplectic form gives rise to a natural isomorphism between the tangent space and the cotangent space at a point, associating to any tangent covector a canonical tangent vector.
Definition as linear functionals
Let M be a smooth manifold and let x be a point in M. Let TxM be the tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at x. Then the cotangent space at x is defined as the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of TxM:
- Tx*M = (TxM)*
Concretely, elements of the cotangent space are linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s on TxM. That is, every element α ∈ Tx*M is a linear map
- α : TxM → F
where F is the underlying field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of the vector space being considered. In most cases, this is the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. The elements of Tx*M are called cotangent vectors.
Alternative definition
In some cases, one might like to have a direct definition of the cotangent space without reference to the tangent space. Such a definition can be formulated in terms of equivalence classes of smooth functions on M. Informally, we will say that two smooth functions f and g are equivalent at a point x if they have the same first-order behavior near x. The cotangent space will then consist of all the possible first-order behaviors of a function near x.Let M be a smooth manifold and let x be a point in M. Let Ix be the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of all functions in C∞(M) vanishing at x, and let Ix2 be the set of functions of the form
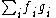, where fi, gi ∈ Ix. Then Ix and Ix2 are real vector spaces and the cotangent space is defined as the quotient spaceQuotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
Tx*M = Ix / Ix2.
This formulation is analogous to the construction of the cotangent space to define the Zariski tangent space
Zariski tangent space
In algebraic geometry, the Zariski tangent space is a construction that defines a tangent space at a point P on an algebraic variety V...
in algebraic geometry. The construction also generalizes to locally ringed spaces.
The differential of a function
Let M be a smooth manifold and let f ∈ C∞(M) be a smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. The differential of f at a point x is the map
- dfx(Xx) = Xx(f)
where Xx is a tangent vector
Differential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
at x, thought of as a derivation. That is
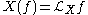is the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
of f in the direction X, and one has df(X)=X(f). Equivalently, we can think of tangent vectors as tangents to curves, and write
- dfx(γ′(0)) = (f o γ)′(0)
In either case, dfx is a linear map on TxM and hence it is a tangent covector at x.
We can then define the differential map d : C∞(M) → Tx*M at a point x as the map which sends f to dfx. Properties of the differential map include:
- d is a linear map: d(af + bg) = a df + b dg for constants a and b,
- d(fg)x = f(x)dgx + g(x)dfx,
The differential map provides the link between the two alternate definitions of the cotangent bundle given above. Given a function f ∈ Ix (a smooth function vanishing at x) we can form the linear functional dfx as above. Since the map d restricts to 0 on Ix2 (the reader should verify this), d descends to a map from Ix / Ix2 to the dual of the tangent space, (TxM)*. One can show that this map is an isomorphism, establishing the equivalence of the two definitions.
The pullback of a smooth map
Just as every differentiable map f : M → N between manifolds induces a linear map (called the pushforward or derivative) between the tangent spaces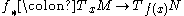every such map induces a linear map (called the pullback) between the cotangent spaces, only this time in the reverse direction:
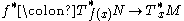
The pullback is naturally defined as the dual (or transpose) of the pushforward. Unraveling the definition, this means the following:
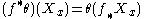
where θ ∈ Tf(x)*N and Xx ∈ TxM. Note carefully where everything lives.
If we define tangent covectors in terms of equivalence classes of smooth maps vanishing at a point then the definition of the pullback is even more straightforward. Let g be a smooth function on N vanishing at f(x). Then the pullback of the covector determined by g (denoted dg) is given by
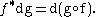
That is, it is the equivalence class of functions on M vanishing at x determined by g o f.
Exterior powers
The k-th exterior power of the cotangent space, denoted Λk(Tx*M), is another important object in differential geometry. Vectors in the kth exterior power, or more precisely sections of the k-th exterior power of the cotangent bundleCotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, are called differential k-forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
. They can be thought of as alternating, multilinear maps on k tangent vectors.
For this reason, tangent covectors are frequently called one-form
One-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
s.