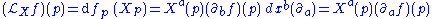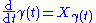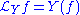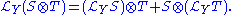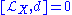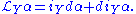Lie derivative
Encyclopedia
In mathematics
, the Lie derivative (icon), named after Sophus Lie
by Władysław Ślebodziński, evaluates the change of a vector field
or more generally a tensor field
, along the flow
of another vector field. This change is coordinate invariant and therefore the Lie derivative is defined on any differentiable manifold
.
The Lie derivative along a vector field is the evaluation of the vector field on functions, and a derivation
on the algebra
of tensor field
s over a manifold M. It also commutes with contraction and the exterior derivative on differential forms. This uniquely determines the Lie derivative and it follows that for vector fields the Lie derivative is the commutator
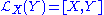
It also shows that the Lie derivatives on M are an infinite-dimensional Lie algebra
representation of the Lie algebra of vector fields with the Lie bracket
defined by the commutator,
.
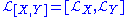Considering vector fields as infinitesimal generator
s of flows (active diffeomorphism
s) on M, the Lie Derivatives are the infinitesimal representation of the representation of the diffeomorphism group on tensor fields, analogous to Lie algebra representations as infinitesimal representations associated to group representation in Lie group
theory.
Generalisations exist for spinor
fields, fibre bundles with connection
and vector valued differential forms.
, we begin by defining the Lie derivative acting on scalar functions and vector fields. The Lie derivative can also be defined to act on general tensors, as developed later in the article.
of a pair of vector fields X and Y. There are several approaches to defining the Lie bracket, all of which are equivalent. Regardless of the chosen definition, one then defines the Lie derivative of the vector field Y to be equal to the Lie bracket of X and Y, that is,
.
Other equivalent definitions are (here,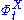
is the flow transformation
and d the tangent map derivative operator):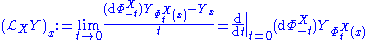
. Both the Lie derivative and the exterior derivative attempt to capture the idea of a derivative in different ways. These differences can be bridged by introducing the idea of an antiderivation or equivalently an interior product, after which the relationships fall out as a set of identities.
Let M be a manifold and X a vector field on M. Let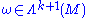
be a k+1-form. The interior product of X and ω is
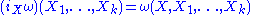
Note that
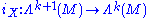
and that
is a 
-antiderivation
. That is,
is R-linear, and
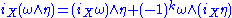
for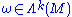
and η another differential form. Also, for a function 
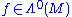, that is a real or complex-valued function on M, one has
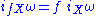
The relationship between exterior derivative
s and Lie derivatives can then be summarized as follows. For an ordinary function f, the Lie derivative is just the contraction of the exterior derivative with the vector field X:
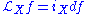
For a general differential form, the Lie derivative is likewise a contraction, taking into account the variation in X:
.
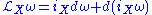This identity is known variously as "Cartan's formula" or "Cartan's magic formula," and shows in particular that:
.
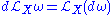The derivative of products is distributed:
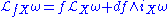
be the algebra
of functions defined on the manifold
M. Then
is a derivation
on the algebra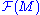
. That is,
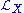is R-linear and
.
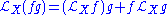Similarly, it is a derivation on
where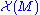 
is the set of vector fields on M:
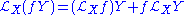
which may also be written in the equivalent notation
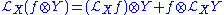
where the tensor product
symbol
is used to emphasize the fact that the product of a function times a vector field is being taken over the entire manifold.
Additional properties are consistent with that of the Lie bracket
. Thus, for example, considered as a derivation on a vector field,
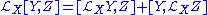
one finds the above to be just the Jacobi identity
. Thus, one has the important result that the space of vector fields over M, equipped with the Lie bracket, forms a Lie algebra
.
The Lie derivative also has important properties when acting on differential forms. Let α and β be two differential forms on M, and let X and Y be two vector fields. Then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Lie derivative (icon), named after Sophus Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
by Władysław Ślebodziński, evaluates the change of a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
or more generally a tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
, along the flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
of another vector field. This change is coordinate invariant and therefore the Lie derivative is defined on any differentiable manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
The Lie derivative along a vector field is the evaluation of the vector field on functions, and a derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
on the algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
s over a manifold M. It also commutes with contraction and the exterior derivative on differential forms. This uniquely determines the Lie derivative and it follows that for vector fields the Lie derivative is the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
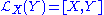
It also shows that the Lie derivatives on M are an infinite-dimensional Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
representation of the Lie algebra of vector fields with the Lie bracket
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
defined by the commutator,
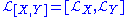.Considering vector fields as infinitesimal generator
Infinitesimal generator
In mathematics, the term infinitesimal generator may refer to:* an element of the Lie algebra associated to a Lie group;* the infinitesimal generator of a stochastic process;* the infinitesimal generator of a strongly continuous semigroup....
s of flows (active diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s) on M, the Lie Derivatives are the infinitesimal representation of the representation of the diffeomorphism group on tensor fields, analogous to Lie algebra representations as infinitesimal representations associated to group representation in Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
theory.
Generalisations exist for spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
fields, fibre bundles with connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
and vector valued differential forms.
Definition
The Lie derivative may be defined in several equivalent ways. In this section, to keep things simpleKISS principle
KISS is an acronym for the design principle Keep it simple, Stupid!. Other variations include "keep it simple and stupid", "keep it short and simple", "keep it simple sir", "keep it simple or be stupid" or "keep it simple and straightforward"...
, we begin by defining the Lie derivative acting on scalar functions and vector fields. The Lie derivative can also be defined to act on general tensors, as developed later in the article.
The Lie derivative of a function
There are several equivalent definitions of a Lie derivative of a function.- The Lie derivative can be defined in terms of the definition of vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s as first order differential operators. Given a function and a vector field X defined on M, the Lie derivative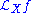
of a function ƒ along a vector field 
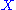is simply the application of the vector field. It can be interpreted as the directional derivativeDirectional derivativeIn mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of f along X. Hence at a point we have
-
.
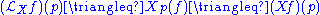- By the definition of the differentialDifferential (calculus)In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
of a function on M the definition can also be written as
.
- Choosing local coordinates xa, and writing :
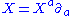, where, the 
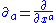are a local basis vectors for the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, we have locally
.
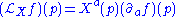- Likewise
is the 1-form locally given by 
. which implies
- recovering the original definition.
- Alternatively, the Lie derivative can be defined as
-
- where
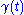is a curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
on M such that - for the smooth vector field X on M with
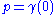. The existence of solutions to this first-order ordinary differential equationOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
is given by the Picard–Lindelöf theoremPicard–Lindelöf theoremIn mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
(more generally, the existence of such curves is given by the Frobenius theoremFrobenius theorem (differential topology)In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
).
The Lie derivative of a vector field
The Lie derivative can be defined for vector fields by first defining the Lie bracketLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of a pair of vector fields X and Y. There are several approaches to defining the Lie bracket, all of which are equivalent. Regardless of the chosen definition, one then defines the Lie derivative of the vector field Y to be equal to the Lie bracket of X and Y, that is,.Other equivalent definitions are (here,
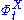is the flow transformationFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
and d the tangent map derivative operator):
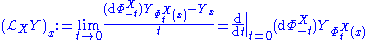
The Lie derivative of differential forms
The Lie derivative can also be defined on differential forms. In this context, it is closely related to the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
. Both the Lie derivative and the exterior derivative attempt to capture the idea of a derivative in different ways. These differences can be bridged by introducing the idea of an antiderivation or equivalently an interior product, after which the relationships fall out as a set of identities.
Let M be a manifold and X a vector field on M. Let
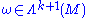be a k+1-form. The interior product of X and ω is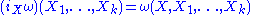Note that
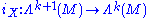
and that
is a -antiderivationDerivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
. That is,
is R-linear, and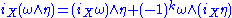for
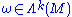and η another differential form. Also, for a function 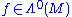, that is a real or complex-valued function on M, one has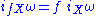The relationship between exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
s and Lie derivatives can then be summarized as follows. For an ordinary function f, the Lie derivative is just the contraction of the exterior derivative with the vector field X:
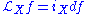
For a general differential form, the Lie derivative is likewise a contraction, taking into account the variation in X:
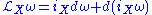.This identity is known variously as "Cartan's formula" or "Cartan's magic formula," and shows in particular that:
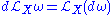.The derivative of products is distributed:
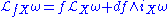
Properties
The Lie derivative has a number of properties. Let be the algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
of functions defined on the manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M. Then
is a derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
on the algebra
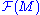. That is, 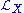is R-linear and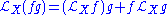.Similarly, it is a derivation on
where 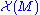is the set of vector fields on M: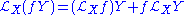which may also be written in the equivalent notation
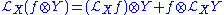
where the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
symbol
is used to emphasize the fact that the product of a function times a vector field is being taken over the entire manifold.Additional properties are consistent with that of the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
. Thus, for example, considered as a derivation on a vector field,
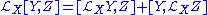
one finds the above to be just the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. Thus, one has the important result that the space of vector fields over M, equipped with the Lie bracket, forms a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
.
The Lie derivative also has important properties when acting on differential forms. Let α and β be two differential forms on M, and let X and Y be two vector fields. Then
-
-
-
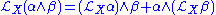
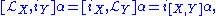where i denotes interior product defined above and it's clear whether [.,.] denotes the commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
or the Lie bracket of vector fieldsLie bracket of vector fieldsIn the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
.
Lie derivative of tensor fields
More generally, if we have a differentiable tensor field T of rank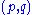
and a differentiable vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
Y (i.e. a differentiable section of the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM), then we can define the Lie derivative of T along Y. Let φ:M×R→M be the one-parameter semigroup of local diffeomorphisms of M induced by the vector flowVector flowIn mathematics, the vector flow refers to a set of closely related concepts of the flow determined by a vector field. These appear in a number of different contexts, including differential topology, Riemannian geometry and Lie group theory...
of Y and denote φt(p) := φ(p, t). For each sufficiently small t, φt is a diffeomorphism from a neighborhood in M to another neighborhood in M, and φ0 is the identity diffeomorphism. The Lie derivative of T is defined at a point p by
.
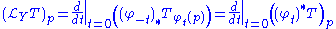where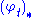
is the pushforward along the diffeomorphism and 
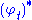is the pullback along the diffeomorphism. Intuitively, if you have a tensor field 
and a vector field Y, then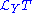 
is the infinitesimal change you would see when you flow 
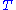using the vector field -Y, which is the same thing as the infinitesimal change you would see in 
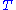if you yourself flowed along the vector field Y.
We now give an algebraic definition. The algebraic definition for the Lie derivative of a tensor field follows from the following four axioms:
- Axiom 1. The Lie derivative of a function is the directional derivative of the function. So if f is a real valued function on M, then
- Axiom 2. The Lie derivative obeys the Leibniz rule. For any tensor fields S and T, we have
- Axiom 3. The Lie derivative obeys the Leibniz rule with respect to contraction
- Axiom 4. The Lie derivative commutes with exterior derivative on functions
Taking the Lie derivative of the relation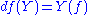
then easily shows that
that the Lie derivative of a vector field is the Lie bracket. So if X is a vector field, one has
The Lie derivative of a differential form is the anticommutator of the interior product with the exterior derivative. So if α is a differential form,
This follows easily by checking that the expression commutes with exterior derivative, is a derivation (being an anticommutator of graded derivations) and does the right thing on functions.
Explicitly, let T be a tensor field of type (p,q). Consider T to be a differentiable multilinear map of smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
sectionsSection (fiber bundle)In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
α1, α2, ..., αq of the cotangent bundle T*M and of sections X1, X2, ... Xp of the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM, written T(α1, α2, ..., X1, X2, ...) into R. Define the Lie derivative of T along Y by the formula
-
-
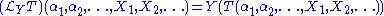
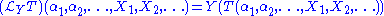
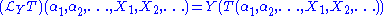
The analytic and algebraic definitions can be proven to be equivalent using the properties of the pushforward and the Leibniz rule for differentiation. Note also that the Lie derivative commutes with the contraction.
Coordinate expressions
In local coordinate notation, for a type (r,s) tensor field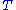
, the Lie derivative along 
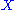is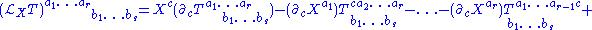
-
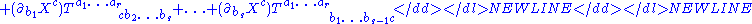
here, the notation
means taking the partial derivative with respect to the coordinate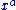 
. Alternatively, if we are using a torsion-free connectionConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
(e.g. the Levi Civita connection), then the partial derivative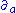
can be replaced with the covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
.
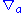The Lie derivative of a tensor is another tensor of the same type, i.e. even though the individual terms in the expression depend on the choice of coordinate system, the expression as a whole results in a tensor
which is independent of any coordinate system.
The definition can be extended further to tensor densities of weight w for any real w. If T is such a tensor density, then its Lie derivative is a tensor density of the same type and weight.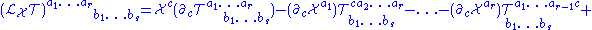
-
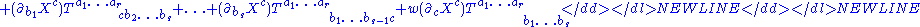
Notice the new term at the end of the expression.
Generalizations
Various generalizations of the Lie derivative play an important role in differential geometry.
The Lie derivative of a spinor field
A definition for Lie derivatives of spinors along
generic spacetime vector fields, not necessarily Killing ones, on a general (pseudo) Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
was
already proposed in 1972 by Yvette Kosmann. Later, it was provided
a geometric framework which justifies her ad hoc prescription within the general framework of
Lie derivatives on fiber bundles in the explicit context of gauge natural bundles
which turn out to be the most appropriate arena for (gauge-covariant) field theories.
In a given spin manifold, that is in a Riemannian manifold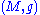
admitting
a spin structureSpin structureIn differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
, the Lie derivative of a spinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
fieldField-Places:* Field, British Columbia, Canada* Field, Minneapolis, Minnesota, United States* Field, Ontario, Canada* Field Island, Nunavut, Canada* Mount Field - Expanses of open ground :* Field...
can be defined
by first defining it with respect to
infinitesimal isometries (Killing vector fields) via the André LichnerowiczAndré LichnerowiczAndré Lichnerowicz was a noted French differential geometer and mathematical physicist of Polish descent.-Biography:...
's local expression given in 1963:
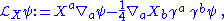
where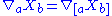
,
as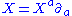
is assumed to be a Killing vector fieldKilling vector fieldIn mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
, and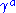
are Dirac matrices.
It is then possible to extend Lichnerowicz's definition to all vector fields (generic infinitesimal transformations)
by retaining Lichnerowicz's local expression for a generic vector field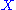
, but explicitly taking
the antisymmetric part of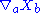
only.
More explicitly, Kosmann's local expression given in 1972 is:
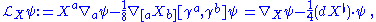
where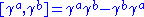
is the commutator, 
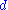is exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
,
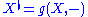is the dual 1 form corresponding to 
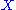under the metric (i.e. with lowered indices) and 
is Clifford multiplication.
It is worth noting that the spinor Lie derivative is independent of the metric, and hence the connection. This is not obvious from the right-hand side of Kosmann's local expression, as the right-hand side seems to depend on the metric through the spin connection (covariant derivative), the dualisation of vector fields (lowering of the indices) and the Clifford multiplication on the spinor bundle. Such is not the case: the quantities on the right-hand side of Kosmann's local expression combine so as to make all metric and connection dependent terms cancel.
To gain a better understanding of the long-debated concept of Lie derivative of spinor fields see and the original article, where the definition of a Lie derivative of spinor
fields is placed in the more general framework of the theory of Lie derivatives
of sections of fiber bundles and the direct approach by Y. Kosmann to the spinor
case is generalized to gauge natural bundles in the form of a new geometric concept
called the Kosmann lift.
Covariant Lie derivative
If we have a principal bundle over the manifold M with G as the structure group, and we pick X to be a covariant vector field as section of the tangent space of the principal bundle (i.e. it has horizontal and vertical components), then the covariant Lie derivative is just the Lie derivative with respect to X over the principal bundle.
Now, if we're given a vector field Y over M (but not the principal bundle) but we also have a connectionConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
over the principal bundle, we can define a vector field X over the principal bundle such that its horizontal component matches Y and its vertical component agrees with the connection. This is the covariant Lie derivative.
See connection formConnection formIn mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
for more details.
Nijenhuis–Lie derivative
Another generalization, due to Albert NijenhuisAlbert NijenhuisAlbert Nijenhuis is a Dutch mathematician at the University of Washington and the University of Pennsylvania working on combinatorics and differential geometry, who introduced the Nijenhuis tensor , the Schouten-Nijenhuis bracket , the Frölicher-Nijenhuis bracket , and the Nijenhuis-Richardson...
, allows one to define the Lie derivative of a differential form along any section of the bundle Ωk(M, TM) of differential forms with values in the tangent bundle. If K ∈ Ωk(M, TM) and α is a differential p-form, then it is possible to define the interior product iKα of K and α. The Nijenhuis–Lie derivative is then the anticommutator of the interior product and the exterior derivative: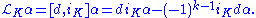
See also
- Covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
- Connection (mathematics)Connection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
- Frölicher–Nijenhuis bracket
- GeodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
- Killing fieldKilling vector fieldIn mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
- Covariant derivative
-
-
-
-
