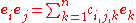Algebra over a field
Encyclopedia
In mathematics
, an algebra over a field
is a vector space
equipped with a bilinear vector product. That is to say, it is
an algebraic structure
consisting of a vector space together with an operation
, usually called multiplication
, that combines any two vectors to form a third vector; to qualify as an algebra, this multiplication must satisfy certain compatibility axiom
s with the given vector space structure, such as distributivity
. In other words, an algebra over a field is a set together with operations of multiplication, addition
, and scalar multiplication by elements of the field.
One may generalize this notion by replacing the field of scalars by a commutative ring
, and thus defining an algebra over a ring
.
Note that while some authors may use the term "algebra" to describe a unital "associative algebra
", this will not be the case for this article.
may be written a + bi, where a and b are real number
s and i is the imaginary unit
. In other words, a complex number is represented by the vector (a, b) over the field of real numbers. So the complex numbers form a two-dimensional real vector space, where addition is given by (a, b) + (c, d) = (a + c, b + d) and scalar multiplication is given by c(a, b) = (ca, cb), where all of a, b, c and d are real numbers. We use the symbol · to multiply two vectors together, which we use complex multiplication to define: (a, b) · (c, d) = (ac − bd, ad + bc).
The following statements are basic properties of the complex numbers. Let x, y, z be complex numbers, and let a, b be real numbers.
This example fits into the following definition by taking the field K to be the real numbers, and the vector space A to be the complex numbers.
over K equipped with an additional binary operation
from A × A to A, denoted here by · (i.e. if x and y are any two elements of A, x · y is the product of x and y). Then A is an algebra over K if the following identities hold for any three elements x, y, and z of A, and all elements ("scalar
s") a and b of K:
These three axioms are another way of saying that the binary operation is bilinear
. An algebra over K is sometimes also called a K-algebra, and K is called the base field of A. The binary operation is often referred to as multiplication in A. The convention adopted in this article is that multiplication of elements of an algebra is not necessarily associative
, although some authors use the term algebra to refer to an associative algebra
.
Notice that when a binary operation on a vector space is commutative, as in the above example of the complex numbers, it is left distributive exactly when it is right distributive. But in general, for non-commutative operations (such as the next example of the quaternions), they are not equivalent, and therefore require separate axioms.
has an inverse
. It is natural to ask whether one can similarly define a multiplication on a three dimensional real vector space such that every non-zero element has an inverse. The answer is no (see normed division algebra
s).
Nevertheless, in 1843, the quaternions were defined and provided the now famous four dimensional example of an algebra over the real numbers, where one can not only multiply vectors, but also divide. Any quaternion may be written as (a, b, c, d) = a + bi + cj + dk. Unlike the complex numbers, the quaternions are an example of a non-commutative
algebra: for instance, (0,1,0,0) · (0,0,1,0) = (0,0,0,1) but (0,0,1,0) · (0,1,0,0) = (0,0,0,-1).
The quaternions were soon followed by several other hypercomplex number
systems, which were the early examples of algebras over a field.
is a K-linear map f: A → B such that f(xy) = f(x) f(y) for all x,y in A. The space of all K-algebra homomorphisms is frequently written as
A K-algebra isomorphism
is a bijective K-algebra morphism. For all practical purposes, isomorphic algebras differ only by notation.
that has the property that the product of any two of its elements is again in the subspace. In other words, a subalgebra of an algebra is a subset of elements that is closed under addition, multiplication, and scalar multiplication. In symbols, we say that a subset L of a K-algebra A is a subalgebra if for every x, y in L and c in K, we have that x · y, x + y, and cx are all in L.
In the above example of the complex numbers viewed as a two-dimensional algebra over the real numbers, the one-dimensional real line is a subalgebra.
A left ideal of a K-algebra is a linear subspace that has the property that any element of the subspace multiplied on the left by any element of the algebra produces an element of the subspace. In symbols, we say that a subset L of a K-algebra A is a left ideal if for every x and y in L, z in A and c in K, we have the following three statements.
If (3) were replaced with x · z is in L, then this would define a right ideal. A two-sided ideal is a subset that is both a left and a right ideal. The term ideal on its own is usually taken to mean a two-sided ideal. Of course when the algebra is commutative, then all of these notions of ideal are equivalent. Notice that conditions (1) and (2) together are equivalent to L being a linear subspace of A. It follows from condition (3) that every left or right ideal is a subalgebra.
It is important to notice that this definition is different from the definition of an ideal of a ring
, in that here we require the condition (2). Of course if the algebra is unital, then condition (3) implies condition (2).
F/K, which is to say a bigger field F that contains K, then there is a natural way to construct an algebra over F from any algebra over K. It is the same construction one uses to make a vector space over a bigger field, namely the tensor product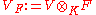
. So if A is an algebra over K, then 
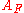is an algebra over F.
or associativity
of the multiplication operation, which are not required in the broad definition of an algebra. The theories corresponding to the different types of algebras are often very different.
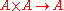. There are left and right multiplication maps
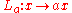and 
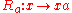. The enveloping algebra of A is the subalgebra of all K-endomorphisms of A generated by the multiplication maps.
An algebra is unital or unitary if it has a unit or identity element I with Ix = x = xI for all x in the algebra.
The best-known kinds of non-associative algebras are nearly associative—that is, some simple equation constrains the differences between different ways of associating multiplication of elements. These include:
These properties are related by: associative implies alternative, which in turn implies power associative; commutative and associative implies Jordan, which implies power associative. None of the converse implications hold.
A together with a ring homomorphism
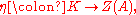
where Z(A) is the center
of A. Since η is a ring morphism, then one must have either that A is the trivial ring, or that η is injective
. This definition is equivalent to that above, with scalar multiplication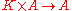
given by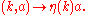
Given two such associative unital K-algebras A and B, a unital K-algebra morphism f: A → B is a ring morphism that commutes with the scalar multiplication defined by η, which one may write as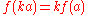
for all
and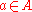 
. In other words, the following diagram commutes: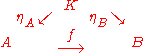
elements of A.
Conversely, once a basis for A has been chosen, the products of basis elements can be set arbitrarily, and then extended in a unique way to a bilinear operator on A, i.e., so the resulting multiplication satisfies the algebra laws.
Thus, given the field K, any algebra can be specified up to
isomorphism
by giving its dimension (say n), and specifying n3 structure coefficients ci,j,k, which are scalars
.
These structure coefficients determine the multiplication in A via the following rule:
where e1,...,en form a basis of A.
The only requirement on the structure coefficients is that, if the dimension n is infinite, then this sum must always converge (in whatever sense is appropriate for the situation).
Note however that several different sets of structure coefficients can give rise to isomorphic algebras.
When the algebra can be endowed with a metric
, then the structure coefficients are written with upper and lower indices, so as to distinguish their transformation properties under coordinate transformations. Specifically, lower indices are covariant indices, and transform via pullbacks, while upper indices are contravariant, transforming under pushforwards. Thus, in mathematical physics
, the structure coefficients are often written ci,jk, and their defining rule is written using the Einstein notation
as
If you apply this to vectors written in index notation
, then this becomes
If K is only a commutative ring and not a field, then the same process works if A is a free module
over K. If it isn't, then the multiplication is still completely determined by its action on a set that spans A; however, the structure constants can't be specified arbitrarily in this case, and knowing only the structure constants does not specify the algebra up to isomorphism.
.
There exist two two-dimensional algebras. Each algebra consists of linear combinations (with complex coefficients) of two basis elements, 1 (the unit) and a. According to the definition of a unit,
It remains to specify
for the first algebra,
for the second algebra.
There exist five three-dimensional algebras. Each algebra consists of linear combinations of three basis elements, 1 (the unit), a and b. Taking into account the definition of a unit, it is sufficient to specify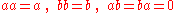
for the first algebra,
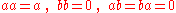for the second algebra,
for the third algebra,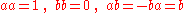
for the fourth algebra,
for the fifth algebra.
The fourth algebra is non-commutative, others are commutative.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebra over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
equipped with a bilinear vector product. That is to say, it is
an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
consisting of a vector space together with an operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, usually called multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, that combines any two vectors to form a third vector; to qualify as an algebra, this multiplication must satisfy certain compatibility axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s with the given vector space structure, such as distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
. In other words, an algebra over a field is a set together with operations of multiplication, addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, and scalar multiplication by elements of the field.
One may generalize this notion by replacing the field of scalars by a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, and thus defining an algebra over a ring
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
.
Note that while some authors may use the term "algebra" to describe a unital "associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
", this will not be the case for this article.
First example: The complex numbers
Any complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
may be written a + bi, where a and b are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. In other words, a complex number is represented by the vector (a, b) over the field of real numbers. So the complex numbers form a two-dimensional real vector space, where addition is given by (a, b) + (c, d) = (a + c, b + d) and scalar multiplication is given by c(a, b) = (ca, cb), where all of a, b, c and d are real numbers. We use the symbol · to multiply two vectors together, which we use complex multiplication to define: (a, b) · (c, d) = (ac − bd, ad + bc).
The following statements are basic properties of the complex numbers. Let x, y, z be complex numbers, and let a, b be real numbers.
- (x + y) · z = (x · z) + (y · z). In other words, multiplying a complex number by the sum of two other complex numbers, is the same as multiplying by each number in the sum, and then adding.
- (ax) · (by) = (ab)(x · y). This shows that complex multiplication is compatible with the scalar multiplication by the real numbers.
This example fits into the following definition by taking the field K to be the real numbers, and the vector space A to be the complex numbers.
Definition
Let K be a field, and let A be a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over K equipped with an additional binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
from A × A to A, denoted here by · (i.e. if x and y are any two elements of A, x · y is the product of x and y). Then A is an algebra over K if the following identities hold for any three elements x, y, and z of A, and all elements ("scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s") a and b of K:
- Left distributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
: (x + y) · z = x · z + y · z - Right distributivity: x · (y + z) = x · y + x · z
- Compatibility with scalars: (ax) · (by) = (ab)(x · y).
These three axioms are another way of saying that the binary operation is bilinear
Bilinear operator
In mathematics, a bilinear operator is a function combining elements of two vector spaces to yield an element of a third vector space that is linear in each of its arguments. Matrix multiplication is an example.-Definition:...
. An algebra over K is sometimes also called a K-algebra, and K is called the base field of A. The binary operation is often referred to as multiplication in A. The convention adopted in this article is that multiplication of elements of an algebra is not necessarily associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, although some authors use the term algebra to refer to an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
.
Notice that when a binary operation on a vector space is commutative, as in the above example of the complex numbers, it is left distributive exactly when it is right distributive. But in general, for non-commutative operations (such as the next example of the quaternions), they are not equivalent, and therefore require separate axioms.
A motivating example: quaternions
The real numbers may be viewed as a one dimensional vector space with a compatible multiplication, and hence a one dimensional algebra over itself. We saw above that the complex numbers form a two dimensional vector space over the field of real numbers, and hence form a two dimension algebra over the reals. In both these examples, every non-zero vectorNull vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
has an inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
. It is natural to ask whether one can similarly define a multiplication on a three dimensional real vector space such that every non-zero element has an inverse. The answer is no (see normed division algebra
Normed division algebra
In mathematics, a normed division algebra A is a division algebra over the real or complex numbers which is also a normed vector space, with norm || · || satisfying the following property:\|xy\| = \|x\| \|y\| for all x and y in A....
s).
Nevertheless, in 1843, the quaternions were defined and provided the now famous four dimensional example of an algebra over the real numbers, where one can not only multiply vectors, but also divide. Any quaternion may be written as (a, b, c, d) = a + bi + cj + dk. Unlike the complex numbers, the quaternions are an example of a non-commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
algebra: for instance, (0,1,0,0) · (0,0,1,0) = (0,0,0,1) but (0,0,1,0) · (0,1,0,0) = (0,0,0,-1).
The quaternions were soon followed by several other hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
systems, which were the early examples of algebras over a field.
Algebra homomorphisms
Given K-algebras A and B, a K-algebra homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
is a K-linear map f: A → B such that f(xy) = f(x) f(y) for all x,y in A. The space of all K-algebra homomorphisms is frequently written as
A K-algebra isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
is a bijective K-algebra morphism. For all practical purposes, isomorphic algebras differ only by notation.
Subalgebras and ideals
A subalgebra of an algebra over a field K, is a linear subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
that has the property that the product of any two of its elements is again in the subspace. In other words, a subalgebra of an algebra is a subset of elements that is closed under addition, multiplication, and scalar multiplication. In symbols, we say that a subset L of a K-algebra A is a subalgebra if for every x, y in L and c in K, we have that x · y, x + y, and cx are all in L.
In the above example of the complex numbers viewed as a two-dimensional algebra over the real numbers, the one-dimensional real line is a subalgebra.
A left ideal of a K-algebra is a linear subspace that has the property that any element of the subspace multiplied on the left by any element of the algebra produces an element of the subspace. In symbols, we say that a subset L of a K-algebra A is a left ideal if for every x and y in L, z in A and c in K, we have the following three statements.
- 1) x + y is in L (L is closed under addition),
- 2) cx is in L (L is closed under scalar multiplication),
- 3) z · x is in L (L is closed under left multiplication by arbitrary elements).
If (3) were replaced with x · z is in L, then this would define a right ideal. A two-sided ideal is a subset that is both a left and a right ideal. The term ideal on its own is usually taken to mean a two-sided ideal. Of course when the algebra is commutative, then all of these notions of ideal are equivalent. Notice that conditions (1) and (2) together are equivalent to L being a linear subspace of A. It follows from condition (3) that every left or right ideal is a subalgebra.
It is important to notice that this definition is different from the definition of an ideal of a ring
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, in that here we require the condition (2). Of course if the algebra is unital, then condition (3) implies condition (2).
Extension of scalars
If we have a field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
F/K, which is to say a bigger field F that contains K, then there is a natural way to construct an algebra over F from any algebra over K. It is the same construction one uses to make a vector space over a bigger field, namely the tensor product
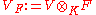. So if A is an algebra over K, then 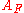is an algebra over F.Kinds of algebras and examples
Algebras over fields come in many different types. These types are specified by insisting on some further axioms, such as commutativityCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
or associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of the multiplication operation, which are not required in the broad definition of an algebra. The theories corresponding to the different types of algebras are often very different.
Associative algebras
- the algebra of all n-by-n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over the field (or commutative ring) K. Here the multiplication is ordinary matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. - Group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
s, where a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
serves as a basis of the vector space and algebra multiplication extends group multiplication. - the commutative algebra K[x] of all polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s over K. - algebras of functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s, such as the R-algebra of all real-valued continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
functions defined on the intervalInterval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0,1], or the C-algebra of all holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s defined on some fixed open set in the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. These are also commutative. - Incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
s are built on certain partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s. - algebras of linear operators, for example on a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. Here the algebra multiplication is given by the composition of operators. These algebras also carry a topologyTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
; many of them are defined on an underlying Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, which turns them into Banach algebraBanach algebraIn mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s. If an involution is given as well, we obtain B*-algebras and C*-algebras. These are studied in functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
Non-associative algebras
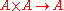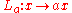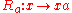A non-associative algebra (or distributive algebra) over a field K is a K-vector space A equipped with a K-bilinear map. There are left and right multiplication maps and . The enveloping algebra of A is the subalgebra of all K-endomorphisms of A generated by the multiplication maps.An algebra is unital or unitary if it has a unit or identity element I with Ix = x = xI for all x in the algebra.
The best-known kinds of non-associative algebras are nearly associative—that is, some simple equation constrains the differences between different ways of associating multiplication of elements. These include:
- Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s that are anticommutativeAnticommutativityIn mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...
, which require xx = 0 and the Jacobi identityJacobi identityIn mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
(xy)z + (yz)x + (zx)y = 0. For these algebras the product is called the Lie bracket and is conventionally written [x,y] instead of xy. Examples include:- Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3 with multiplication given by the vector cross product (with K the field R of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s); - algebras of vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s on a differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
(if K is R or the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C) or an algebraic varietyAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
(for general K); - every associative algebra gives rise to a Lie algebra by using the commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
as Lie bracket. In fact every Lie algebra can either be constructed this way, or is a subalgebra of a Lie algebra so constructed.
- Euclidean space
- Jordan algebraJordan algebraIn abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
s that are commutativeCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and satisfy the Jordan property (xy)x2 = x(yx2) and also xy = yx.- every associative algebra over a field of characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
other than 2 gives rise to a Jordan algebra by defining a new multiplication x*y = (1/2)(xy + yx). In contrast to the Lie algebra case, not every Jordan algebra can be constructed this way. Those that can are called special.
- every associative algebra over a field of characteristic
- Alternative algebraAlternative algebraIn abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
s, which require that (xx)y = x(xy) and (yx)x = y(xx). The most important examples are the octonions (an algebra over the reals), and generalizations of the octonions over other fields. (Obviously all associative algebras are alternative.) Up to isomorphism the only finite-dimensional real alternative, division algebras (see below) are the reals, complexes, quaternions and octonions.
- Power-associative algebras, which require that xmxn = xm+n, where m ≥ 1 and n ≥ 1. (Here we formally define xn recursively as x(xn−1).) Examples include all associative algebras, all alternative algebras, and the sedenionSedenionIn abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
s.
These properties are related by: associative implies alternative, which in turn implies power associative; commutative and associative implies Jordan, which implies power associative. None of the converse implications hold.
Algebras and rings
The definition of an associative K-algebra with unit is also frequently given in an alternative way. In this case, an algebra over a field K is a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
A together with a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
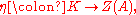
where Z(A) is the center
Center (algebra)
The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
of A. Since η is a ring morphism, then one must have either that A is the trivial ring, or that η is injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
. This definition is equivalent to that above, with scalar multiplication
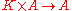
given by
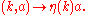
Given two such associative unital K-algebras A and B, a unital K-algebra morphism f: A → B is a ring morphism that commutes with the scalar multiplication defined by η, which one may write as
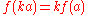
for all
and 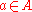. In other words, the following diagram commutes: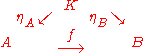Structure coefficients
For algebras over a field, the bilinear multiplication from A × A to A is completely determined by the multiplication of basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
elements of A.
Conversely, once a basis for A has been chosen, the products of basis elements can be set arbitrarily, and then extended in a unique way to a bilinear operator on A, i.e., so the resulting multiplication satisfies the algebra laws.
Thus, given the field K, any algebra can be specified up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
by giving its dimension (say n), and specifying n3 structure coefficients ci,j,k, which are scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
.
These structure coefficients determine the multiplication in A via the following rule:
where e1,...,en form a basis of A.
The only requirement on the structure coefficients is that, if the dimension n is infinite, then this sum must always converge (in whatever sense is appropriate for the situation).
Note however that several different sets of structure coefficients can give rise to isomorphic algebras.
When the algebra can be endowed with a metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, then the structure coefficients are written with upper and lower indices, so as to distinguish their transformation properties under coordinate transformations. Specifically, lower indices are covariant indices, and transform via pullbacks, while upper indices are contravariant, transforming under pushforwards. Thus, in mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the structure coefficients are often written ci,jk, and their defining rule is written using the Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
as
- eiej = ci,jkek.
If you apply this to vectors written in index notation
Index notation
Index notation is used in mathematics and computer programming to specify the elements of matrices or the components of a vector. The formalism of how indices are used varies according to the discipline...
, then this becomes
- (xy)k = ci,jkxiyj.
If K is only a commutative ring and not a field, then the same process works if A is a free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
over K. If it isn't, then the multiplication is still completely determined by its action on a set that spans A; however, the structure constants can't be specified arbitrarily in this case, and knowing only the structure constants does not specify the algebra up to isomorphism.
Classification of low-dimensional algebras
Two-dimensional, three-dimensional and four-dimensional unital associative algebras over the field of complex numbers were completely classified up to isomorphism by Eduard StudyEduard Study
Eduard Study was a German mathematician known for work on invariant theory of ternary forms and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.Study was born in Coburg in the Duchy of...
.
There exist two two-dimensional algebras. Each algebra consists of linear combinations (with complex coefficients) of two basis elements, 1 (the unit) and a. According to the definition of a unit,
It remains to specify
for the first algebra, for the second algebra.There exist five three-dimensional algebras. Each algebra consists of linear combinations of three basis elements, 1 (the unit), a and b. Taking into account the definition of a unit, it is sufficient to specify
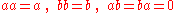for the first algebra, 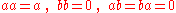for the second algebra, for the third algebra,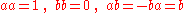 for the fourth algebra, for the fifth algebra.The fourth algebra is non-commutative, others are commutative.
See also
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Differential algebraDifferential algebraIn mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
- Geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
- Max-plus algebraMax-plus algebraA max-plus algebra is an algebra over the real numbers with maximum and addition as the two binary operations.It can be used appropriately to determine marking times within a given Petri net and a vector filled with marking state at the beginning....