Center (algebra)
Encyclopedia
The term center or centre is used in various contexts in abstract algebra
to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:
- The center of a group G consists of all those elements x in G such that xg = gx for all g in G. This is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G. - The center of a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is the subset of R consisting of all those elements x of R such that xr = rx for all r in R. The center is a commutativeCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
subringSubringIn mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of R, and R is an algebraAlgebra (ring theory)In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
over its center. - The center of an algebraAlgebra over a fieldIn mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
A consists of all those elements x of A such that xa = ax for all a in A. See also: central simple algebraCentral simple algebraIn ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
. - The center of a Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
L consists of all those elements x in L such that [x,a] = 0 for all a in L. This is an idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of the Lie algebra L. - The center of a monoidal categoryMonoidal categoryIn mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
C consists of pairs (A,u) where A is an object of C, and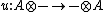
a natural isomorphism satisfying certain axioms.