Ring (mathematics)
Encyclopedia
In mathematics
, a ring is an algebraic structure
consisting of a set together with two binary operations usually called addition
and multiplication
, where the set is an abelian group
under addition (called the additive group of the ring) and a semigroup
under multiplication such that multiplication distributes over addition. In other words the ring axiom
s require that addition is commutative
, addition and multiplication are associative
, multiplication distributes
over addition, each element in the set has an additive inverse
, and there exists an additive identity
. One of the most common examples of a ring is the set of integers endowed with its natural operations of addition and multiplication. Certain variations of the definition of a ring are sometimes employed, and these are outlined later in the article.
The branch of mathematics that studies rings is known as ring theory
. Ring theorists study properties common to both familiar mathematical structure
s such as integer
s and polynomial
s, and to the many less well-known mathematical structures that also satisfy the axioms of ring theory. The ubiquity of rings makes them a central organizing principle of contemporary mathematics.
Ring theory may be used to understand fundamental physical law
s, such as those underlying special relativity
and symmetry phenomena in molecular chemistry
.
The concept of a ring first arose from attempts to prove Fermat's last theorem
, starting with Richard Dedekind
in the 1880s. After contributions from other fields, mainly number theory
, the ring notion was generalized and firmly established during the 1920s by Emmy Noether
and Wolfgang Krull
. Modern ring theory—a very active mathematical discipline—studies rings in their own right. To explore rings, mathematicians have devised various notions
to break rings into smaller, better-understandable pieces, such as ideal
s, quotient ring
s and simple ring
s. In addition to these abstract properties, ring theorists also make various distinctions between the theory of commutative ring
s and noncommutative ring
s—the former belonging to algebraic number theory
and algebraic geometry
. A particularly rich theory has been developed for a certain special class of commutative rings, known as field
s, which lies within the realm of field theory
. Likewise, the corresponding theory for noncommutative rings, that of noncommutative division ring
s, constitutes an active research interest for noncommutative ring theorists. Since the discovery of a mysterious connection between noncommutative ring theory and geometry during the 1980s by Alain Connes
, noncommutative geometry
has become a particularly active discipline in ring theory.
s, Z, consisting of the number
s
together with the usual operations of addition and multiplication. These operations satisfy the following properties:
A ring is a set R equipped with two binary operation
s + : R × R → R and · : R × R → R (where × denotes the Cartesian product
), called addition and multiplication. To qualify as a ring, the set and two operations, (R, +, · ), must satisfy the following requirements known as the ring axioms.
This definition assumes that a binary operation on R is a function
defined on R×R with values in R. Therefore, for any a and b in R, the addition a + b and the product a · b are elements of R.
The most familiar example of a ring is the set of all integer
s, Z = {..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ... }, together with the usual operations of addition and multiplication.
Another familiar example is the set of real number
s R, equipped with the usual addition and multiplication.
Another example of a ring is the set of all square matrices of a fixed size, with real elements, using the matrix addition and multiplication of linear algebra
. In this case, the ring elements 0 and 1 are the zero matrix (with all entries equal to 0) and the identity matrix
, respectively.
4 is defined to be the remainder when x is divided by 4):
It is simple (but tedious) to verify that Z4 is a ring under these operations. First of all, one can use the left-most table to show that Z4 is closed under addition (any result is either 0, 1, 2 or 3). Associativity of addition in Z4 follows from associativity of addition in the set of all integers. The additive identity is 0 as can be verified by looking at the left-most table. Given an integer x, there is always an inverse of x; this inverse is given by 4 - x as one can verify from the additive table. Therefore, Z4 is an abelian group
under addition.
Similarly, Z4 is closed under multiplication as the right-most table shows (any result above is either 0, 1, 2 or 3). Associativity of multiplication in Z4 follows from associativity of multiplication in the set of all integers. The multiplicative identity is 1 as can be verified by looking at the right-most table. Therefore, Z4 is a monoid
under multiplication.
Distributivity of the two operations over each other follow from distributivity of addition over multiplication (and vice-versa) in Z (the set of all integers).
Therefore, this set does indeed form a ring under the given operations of addition and multiplication.
Properties of this ring
0 + 0 = 0
0 × 0 = 0
then one can verify that ({0}, +, ×) forms a ring known as the trivial ring. Since there can be only one result for any product or sum (0), this ring is both closed and associative for addition and multiplication, and furthermore satisfies the distributive law. The additive and multiplicative identities are both equal to 0. Similarly, the additive inverse of 0 is 0. The trivial ring is also a (rather trivial) example of a zero ring
(see below).
of a ring is another ring that uses the "same" operations and is contained in it. More formally, suppose (R, +, ·) is a ring, and S is a subset of R such that
Let '+S' and '·S' denote the operations '+' and '·', restricted to S×S. Then (S, +S, ·S) is a subring of (R, +, ·). Since the restricted operations are completely determined by S and the original ones, the subring is often written simply as (S, +, ·).
For example, a subring of the complex number ring C is any subset of C that includes 1 and is closed under addition, multiplication, and negation, such as:
If A is a subring of R, and B is a subset
of A such that B is also a subring of R, then B is a subring of A.
from a ring (R, +, ·) to a ring (S, ‡, *) is a function f from R to S that commutes with the ring operations; namely, such that, for all a, b in R the following identities hold:
Moreover, the function f must take the identity element 1R of '·' to the identity element 1S of '*'.
(this is not required if identity is not required).
For example, the function that maps each integer x to its remainder modulo 4 (a number in {0, 1, 2, 3}) is a homomorphism from the ring Z to the ring Z4.
A ring homomorphism is said to be an isomorphism if there exists an inverse homomorphism to f (i.e., a ring homomorphism which is an inverse function
). Equivalently, any bijective
ring homomorphism is a ring isomorphism.
in a ring is to somehow allow one to define the quotient ring
of a ring (analogous to the quotient group
of a group
; see below). An ideal in a ring can therefore be thought of as a generalization of a normal subgroup
in a group. More formally, let (R, +, · ) be a ring. A subset
I of R is said to be a right ideal in R if:
A left ideal is similarly defined with the second condition being replaced. More specifically, a subset I of R is a left ideal in R if:
Notes
Examples
The study of rings originated from the theory of polynomial ring
s and the theory of algebraic integer
s. Furthermore, the appearance of hypercomplex number
s in the mid-19th century undercut the pre-eminence of fields
in mathematical analysis.
In the 1880s Richard Dedekind introduced the concept of a ring, and the term ring (Zahlring) was coined by David Hilbert
in 1892 and published in the article Die Theorie der algebraischen Zahlkörper, Jahresbericht der Deutschen Mathematiker Vereinigung, Vol. 4, 1897. According to Harvey Cohn, Hilbert used the term for a specific ring that had the property of "circling directly back" to an element of itself.
The first axiomatic definition of a ring was given by Adolf Fraenkel in an essay in Journal für die reine und angewandte Mathematik (A. L. Crelle), vol. 145, 1914. In 1921, Emmy Noether
gave the first axiomatic foundation of the theory of commutative ring
s in her monumental paper Ideal Theory in Rings.
.
In particular, since the axioms state that (R,+) is a commutative group, all pertinent theorems of group theory
apply, such as the uniqueness of the additive identity and the uniqueness of the additive inverse of a particular element. In the same way one can prove the uniqueness of the inverse of a unit in a ring
.
However, rings also have specific properties that combine addition with multiplication. In any ring (R, +, ⋅):
of a ring, is a generalization of the notion of a quotient group
of a group. More formally, given a ring (R, +, · ) and a two-sided ideal
I of (R, +, · ), the quotient ring (or factor ring) R/I is the set of cosets of I (with respect to the underlying additive group of (R, +, · ); i.e. cosets with respect to (R, +)) together with the operations:
+ (b + I) = (a + b) + I and(b + I) = (ab) + I.
For every a, b in R.
Let (R, +R, ·R) be a ring and let
where the convention that 
is the set of all nonnegative integers, is adopted. Define +S : S × S → S and ·S : S × S → S, as follows (where 
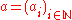and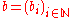 
are arbitrary elements of S):
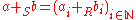
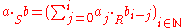
Then (S, +S, ·S) is a ring referred to as the polynomial ring over R.
Notes
Most authors write S as R[X], where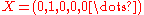
is an element of S. This convention is adopted because if 
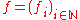is an element of S, and if 
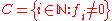, f can be written as a polynomial with coefficients in R, in the variable X, as follows:
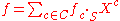
This allows one to view S as merely the set of all polynomials over R in the variable X, with multiplication and addition of polynomials defined in the canonical manner. Therefore, in all that follows, S, denoted by R[X], shall be identified in this fashion. Addition and multiplication in S, and those of the underlying ring R, will be denoted by juxtaposition.
Let (R, +R, ·R) be a ring and let
. Define +M : Mr(R) × Mr(R) → Mr(R) and ·M : Mr(R) × Mr(R) → Mr(R), as follows (where 
and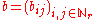 
are arbitrary elements of Mr(R)):
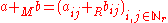
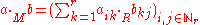
Then (Mr(R), +M, ·M) is a ring referred to as the ring of r×r matrices over R.
Notes
The ring Mr(R) can be viewed as merely the ring of r×r matrices over R with matrix addition and multiplication defined in the canonical manner. For given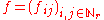
in Mr(R), f can be identified with the r×r matrix whose (i, j)-entry is 
. Therefore, in all that follows, Mr(R) and each of its elements shall be identified in this fashion. Addition and multiplication in Mr(R), and those of the underlying ring R, will be denoted by juxtaposition.
s can be fruitfully analyzed in terms of some associated ring
.
X one can associate its integral cohomology ring
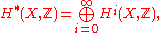
a graded ring. There are also homology groups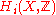
of a space, and indeed these were defined first, as a useful tool for distinguishing between certain pairs of topological spaces, like the sphere
s and tori
, for which the methods of point-set topology are not well-suited. Cohomology groups were later defined in terms of homology groups in a way which is roughly analogous to the dual of a vector space
. To know each individual integral homology group is essentially the same as knowing each individual integral cohomology group, because of the universal coefficient theorem
. However, the advantage of the cohomology groups is that there is a natural product
, which is analogous to the observation that one can multiply pointwise a k-multilinear form and an l-multilinear form to get a (k + l)-mulilinear form.
The ring structure in cohomology provides the foundation for characteristic class
es of fiber bundle
s, intersection theory on manifolds and algebraic varieties
, Schubert calculus
and much more.
is associated its Burnside ring
which uses a ring to describe the various ways the group can act
on a finite set. The Burnside ring's additive group is the free abelian group
whose basis are the transitive actions of the group and whose addition is the disjoint union of the action. Expressing an action in terms of the basis is decomposing an action into its transitive constituents. The multiplication is easily expressed in terms of the representation ring
: the multiplication in the Burnside ring is formed by writing the tensor product of two permutation modules as a permutation module. The ring structure allows a formal way of subtracting one action from another. Since the Burnside ring is contained as a finite index subring of the representation ring, one can pass easily from one to the other by extending the coefficients from integers to the rational numbers.
or Hopf algebra
is associated its representation ring
or "Green ring". The representation ring's additive group is the free abelian group whose basis are the indecomposable modules and whose addition corresponds to the direct sum. Expressing a module in terms of the basis is finding an indecomposable decomposition of the module. The multiplication is the tensor product. When the algebra is semisimple, the representation ring is just the character ring from character theory
, which is more or less the Grothendieck group
given a ring structure.
is associated its function field
. The points of an algebraic variety correspond to valuation ring
s contained in the function field and containing the coordinate ring. The study of algebraic geometry
makes heavy use of commutative algebra
to study geometric concepts in terms of ring-theoretic properties. Birational geometry
studies maps between the subrings of the function field.
has an associated face ring, also called its Stanley–Reisner ring. This ring reflects many of the combinatorial properties of the simplicial complex, so it is of particular interest in algebraic combinatorics
. In particular, the algebraic geometry of the Stanley–Reisner ring was used to characterize the numbers of faces in each dimension of simplicial polytope
s.
and the other is the Galois field.
As with finite group
s, the complexity of the classification depends upon the complexity of the prime factorization of m. If m is the square of a prime, for instance, there are precisely eleven rings having order m. On the other hand, there can be only two groups having order m; both of which are abelian.
The theory of finite rings is more complex than that of finite abelian groups, since any finite abelian group is the additive group of at least two nonisomorphic finite rings: the direct product of copies of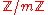
, and the zero ring. On the other hand, the theory of finite rings is simpler than that of not necessarily abelian finite groups. For instance, the classification of finite simple groups
was one of the major breakthroughs of 20th century mathematics, its proof spanning thousands of journal pages. On the other hand, any finite simple ring
is isomorphic to the ring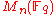
of n by n matrices over a finite field of order q. This follows from two theorems of Joseph Wedderburn
established in 1905 and 1907.
One of these theorems, known as Wedderburn's little theorem
, asserts that any finite division ring
is necessarily commutative. Nathan Jacobson
later discovered yet another condition which guarantees commutativity of a ring:
If for every element r of R there exists an integer such that , then R is commutative.
If, r2 = r for every r, the ring is called a Boolean ring
. More general conditions which guarantee commutativity of a ring are also known.
The number of rings with m elements, for m a natural number, is listed under A027623 in the On-Line Encyclopedia of Integer Sequences
.
is a ring that is also a vector space
over a field K. For instance, the set of n by n matrices over the real field R has dimension n2 as a real vector space, and the matrix multiplication
corresponds to the ring multiplication. For a non-trivial but elementary example consider 2 × 2 real matrices.
is defined to be a ring that is nonassociative
and anticommutative under multiplication, that also satisfies the Jacobi identity
. More specifically we can define a Lie ring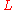
to be an abelian group
under addition with an operation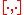
that has the following properties:
Lie rings need not be Lie group
s under addition. Any Lie algebra
is an example of a Lie ring. Any associative ring can be made into a Lie ring by defining a bracket operator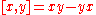
. Conversely to any Lie algebra there is a corresponding ring, called the universal enveloping algebra
.
Lie rings are used in the study of finite p-group
s through the Lazard correspondence. The lower central factors of a p-group are finite abelian p-groups, so modules over Z/pZ. The direct sum of the lower central factors is given the structure of a Lie ring by defining the bracket to be the commutator
of two coset representatives. The Lie ring structure is enriched with another module homomorphism, then pth power map, making the associated Lie ring a so-called restricted Lie ring.
Lie rings are also useful in the definition of a p-adic analytic groups and their endomorphisms by studying Lie algebras over rings of integers such as the p-adic integers. The definition of finite groups of Lie type due to Chevalley involves restricting from a Lie algebra over the complex numbers to a Lie algebra over the integers, and the reducing modulo p to get a Lie algebra over a finite field.
and (X, +, · ) be a ring. Then (X, T, +, · ) is said to be a topological ring
, if its ring structure and topological structure are both compatible (i.e work together) over each other. That is, the addition map (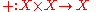
) and the multiplication map ( 
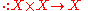) have to be both continuous as maps between topological spaces where X x X inherits the product topology
. So clearly, any topological ring is a topological group
(under addition).
Examples
s. Formally,
Formal definition
Let (R, +, · ) be a ring. Then (R, +, · ) is said to be a commutative ring if for every a, b in R, a · b = b · a. That is, (R, +, · ) is required to be a commutative monoid under multiplication.
Examples
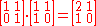, which is not equal to 
Definition
Let R be a ring. Then R is said to be a principal ideal ring (abbreviated PIR), if every ideal in R is of the form a · R = {a · r | r in R}. A principal ideal domain (PID) is a principal ideal ring that is also an integral domain.
The requirement that a ring be a principal ideal domain is somewhat stronger than the other more common properties a ring may satisfy. For example, it is true that if a ring, R, is a unique factorization domain
(UFD), then the polynomial ring
over R is also a UFD. However, such a result does not in general hold for principal ideal rings. For example, the integers are an easy example of a principal ideal ring, but the polynomial ring over the integers fails to be a PIR; if R = Z[x] denotes the polynomial ring over the integers, I = 2 · R + X · R is an ideal which cannot be generated by a single element. Despite this counterexample, the polynomial ring over any field is always a principal ideal domain and in fact, a Euclidean domain
. More generally, a polynomial ring is a PID if and only if the polynomial ring in question is over a field.
Aside from the polynomial ring over a PIR, principal ideal rings possess many interesting properties due to their connection with the integers in terms of divisibility; that is, principal ideal domains behave similarly to the integers with respect to divisibility. For example, any PID is a UFD; i.e., an analogue of the fundamental theorem of arithmetic
holds for principal ideal domains. Furthermore, since Noetherian rings are precisely those rings in which any ideal is finitely generated, principal ideal domains are trivially Noetherian rings. The fact that irreducible elements coincide with prime elements for PID's, together with the fact that every PID is Noetherian, implies that any PID is a UFD. One can also speak of the greatest common divisor of two elements in a PID; if x and y are elements of R, a principal ideal domain, then x · R + y · R = c · R for some c in R since the left-hand side is indeed an ideal. Therefore, c is the desired "GCD" of x and y.
An important class of rings lying in between fields and PID's, is the class of Euclidean domains. In particular, any field is a Euclidean domain, and any Euclidean domain is a PID. An ideal in a Euclidean domain is generated by any element of that ideal with minimum degree (all such elements must be associate). However, not every PID is a Euclidean domain; the ring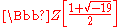
furnishes a counterexample.
holds. Formally,
Definition
Let R be a ring. Then R is said to be a unique factorization domain (abbreviated UFD), if the following conditions are satisfied:
1. R is an integral domain.
2. Every non-zero non-unit
of R is the product of a finite number of irreducible elements.
3. If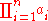
= 
, where all ai's and bj's are irreducible, then n = m and after possible renumbering of the ai's and bj's, bi = ai · ui where ui is a unit
in R.
The second condition above guarantees that "non-trivial" elements of R can be decomposed into irreducibles, and according to the third condition, such a finite decomposition is unique "up to multiplication by unit elements." This weakened form of uniqueness is reasonable to assume for otherwise even the integers would not satisfy the properties of being a UFD ((-2)2 = 22 = 4 demonstrates two "distinct" decompositions of 4; however both decompositions of 4 are equivalent up to multiplication by units (-1 and +1)). The fact that the integers constitute a UFD follows from the fundamental theorem of arithmetic.
For arbitrary rings, one may define a prime element
and an irreducible element
; these two may not in general coincide. However, a prime element in a domain is always irreducible. For UFD's, irreducible elements are also primes.
The class of unique factorization domains is related to other classes of rings. For instance, any Noetherian domain
satisfies conditions 1 and 2 above, but in general Noetherian domains fail to satisfy condition 3. However, if the set of prime elements and the set of irreducible elements coincide for a Noetherian domain, the third condition of a UFD is satisfied. In particular, principal ideal domains are UFD's.
with no zero divisor
s). But we still run into a problem; namely we can't necessarily divide by non-zero elements. For example, the collection of all integers form an integral domain but we still can't divide an integer a by another integer b. For example, 2 cannot divide 3 to obtain another element in this ring. However, this problem can readily be solved if we ensure that every element in the ring has a multiplicative inverse. A field
is a ring in which the non-zero elements form an abelian group
under multiplication. In particular, a field is an integral domain (and therefore has no zero divisors) along with an additional operation of 'division'. Namely, if a and b are in a field F, then a/b is defined to be a · b−1 which is well defined.
Formal definition
Let (R, +, · ) be a ring. Then (R, +, · ) is said to be an integral domain if (R, +, · ) is commutative and has no zero divisors. Furthermore, (R, +, · ) is said to be a field
, if its non-zero elements form an abelian group under multiplication.
Note
Examples
Fields and integral domains are very important in modern algebra.
s is a major area in modern algebra; especially ring theory
. Often noncommutative rings possess interesting invariants that commutative rings do not. As an example, there exist rings which contain non-trivial proper left or right ideals, but are still simple
; that is contain no non-trivial proper (two-sided) ideals. This example illustrates how one must take care when studying noncommutative rings because of possible counterintuitive misconceptions.
The theory of vector space
s is one illustration of a special case of an object studied in noncommutative ring theory. In linear algebra
, the "scalars of a vector space" are required to lie in a field - a commutative division ring
. The concept of a module
, however, requires only that the scalars lie in an abstract ring. Neither commutativity nor the division ring assumption is required on the scalars in this case. Module theory has various applications in noncommutative ring theory, as one can often obtain information about the structure of a ring by making use of its modules. The concept of the Jacobson radical
of a ring; that is, the intersection of all right/left annihilators
of simple
right/left modules over a ring, is one example. The fact that the Jacobson radical can be viewed as the intersection of all maximal right/left ideals in the ring, shows how the internal structure of the ring is reflected by its modules. It is also remarkable that the intersection of all maximal right ideals in a ring is the same as the intersection of all maximal left ideals in the ring, in the context of all rings; whether commutative or noncommutative. Therefore, the Jacobson radical also captures a concept which may seem to be not well-defined for noncommutative rings.
Noncommutative rings serve as an active area of research due to their ubiquity in mathematics. For instance, the ring of n by n matrices over a field
is noncommutative despite its natural occurrence in physics
. More generally, endomorphism ring
s of abelian groups are rarely commutative.
Noncommutative rings, like noncommutative groups, are not very well understood. For instance, although every finite abelian group
is the direct sum of (finite) cyclic group
s of prime-power order, non-abelian groups do not possess such a simple structure. Likewise, various invariants exist for commutative rings, whereas invariants of noncommutative rings are difficult to find. As an example, the nilradical, although "innocent" in nature, need not be an ideal unless the ring is assumed to be commutative. Specifically, the set of all nilpotent elements in the ring of all n x n matrices over a division ring never forms an ideal, irrespective of the division ring chosen. Therefore, the nilradical cannot be studied in noncommutative ring theory. Note however that there are analogues of the nilradical defined for noncommutative rings, that coincide with the nilradical when commutativity is assumed.
One of the best known noncommutative rings is the division ring of quaternions.
in Ab, the category of abelian groups
(thought of as a monoidal category
under the tensor product of
-modules). The monoid action of a ring R on a abelian group is simply an R-module
. Essentially, an R-module is a generalization of the notion of a vector space
- where rather than a vector space over a field, one has a "vector space over a ring".
Let (A, +) be an abelian group and let End(A) be its endomorphism ring
(see above). Note that, essentially, End(A) is the set of all morphisms of A, where if f is in End(A), and g is in End(A), the following rules may be used to compute f + g and f · g:
where + as in f(x) + g(x) is addition in A, and function composition is denoted from right to left. Therefore, associated
to any abelian group, is a ring. Conversely, given any ring, (R, +, · ), (R, +) is an abelian group. Furthermore, for every r in R, right (or left) multiplication by r gives rise to a morphism of (R, +), by right (or left) distributivity. Let A = (R, +). Consider those endomorphism
s of A, that "factor through" right (or left) multiplication of R. In other words, let EndR(A) be the set of all morphisms m of A, having the property that m(r · x) = r · m(x). It was seen that every r in R gives rise to a morphism of A - right multiplication by r. It is in fact true that this association of any element of R, to a morphism of A, as a function from R to EndR(A), is an isomorphism of rings. In this sense, therefore, any ring can be viewed as the endomorphism ring of some abelian X-group (by X-group, it is meant a group with X being its set of operators
). In essence, the most general form of a ring, is the endomorphism group of some abelian X-group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a ring is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
consisting of a set together with two binary operations usually called addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, where the set is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition (called the additive group of the ring) and a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
under multiplication such that multiplication distributes over addition. In other words the ring axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s require that addition is commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, addition and multiplication are associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, multiplication distributes
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over addition, each element in the set has an additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
, and there exists an additive identity
Additive identity
In mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
. One of the most common examples of a ring is the set of integers endowed with its natural operations of addition and multiplication. Certain variations of the definition of a ring are sometimes employed, and these are outlined later in the article.
The branch of mathematics that studies rings is known as ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
. Ring theorists study properties common to both familiar mathematical structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
s such as integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, and to the many less well-known mathematical structures that also satisfy the axioms of ring theory. The ubiquity of rings makes them a central organizing principle of contemporary mathematics.
Ring theory may be used to understand fundamental physical law
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
s, such as those underlying special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and symmetry phenomena in molecular chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
.
The concept of a ring first arose from attempts to prove Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, starting with Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
in the 1880s. After contributions from other fields, mainly number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the ring notion was generalized and firmly established during the 1920s by Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
and Wolfgang Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
. Modern ring theory—a very active mathematical discipline—studies rings in their own right. To explore rings, mathematicians have devised various notions
Glossary of ring theory
Ring theory is the branch of mathematics in which rings are studied: that is, structures supporting both an addition and a multiplication operation. This is a glossary of some terms of the subject.-Definition of a ring:...
to break rings into smaller, better-understandable pieces, such as ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s, quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
s and simple ring
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
s. In addition to these abstract properties, ring theorists also make various distinctions between the theory of commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s and noncommutative ring
Noncommutative ring
In mathematics, more specifically modern algebra and ring theory, a noncommutative ring is a ring whose multiplication is not commutative; that is, if R is a noncommutative ring, there exists a and b in R with a·b ≠ b·a, and conversely.Noncommutative rings are ubiquitous in mathematics, and occur...
s—the former belonging to algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. A particularly rich theory has been developed for a certain special class of commutative rings, known as field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s, which lies within the realm of field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
. Likewise, the corresponding theory for noncommutative rings, that of noncommutative division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
s, constitutes an active research interest for noncommutative ring theorists. Since the discovery of a mysterious connection between noncommutative ring theory and geometry during the 1980s by Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
, noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
has become a particularly active discipline in ring theory.
First example: the integers
The most familiar example of a ring is the set of all integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, Z, consisting of the number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s
- ..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ...
together with the usual operations of addition and multiplication. These operations satisfy the following properties:
- The integers form an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition; that is:- Closure axiom for additionClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
: Given two integers a and b, their sum, a + b is also an integer. - AssociativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of addition: For any integers, a, b and c, (a + b) + c = a + (b + c). So, adding b to a, and then adding c to this result, is the same as adding c to b, and then adding this result to a. - Existence of additive identityIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
: For any integer a, a + 0 = 0 + a = a. Zero is called the identity element of the integers because adding 0 to any integer (in any order) returns the same integer. - Existence of additive inverseInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
: For any integer a, there exists an integer denoted by −a such that a + (−a) = (−a) + a = 0. The element, −a, is called the additive inverse of a because adding a to −a (in any order) returns the identity. - CommutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
of addition: For any two integers a and b, a + b = b + a. So the order in which two integers are added is irrelevant.
- Closure axiom for addition
- The integers form a multiplicative monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
(a monoid under multiplication); that is:- Closure axiom for multiplication: Given two integers a and b, their product, a · b is also an integer.
- Associativity of multiplication: Given any integers, a, b and c, (a · b) · c = a · (b · c). So multiplying b with a, and then multiplying c to this result, is the same as multiplying c with b, and then multiplying a to this result.
- Existence of multiplicative identity: For any integer a, a · 1 = 1 · a = a. So multiplying any integer with 1 (in any order) gives back that integer. One is therefore called the multiplicative identity.
- Multiplication is distributiveDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over addition : These two structures on the integers (addition and multiplication) are compatible in the sense that- a · (b + c) = (a · b) + (a · c), and
- (a + b) · c = (a · c) + (b · c)
- for any three integers a, b and c.
Formal definition
There are some differences in exactly what axioms are used to define a ring. Here one set of axioms for a ring with identity is given, and comments on variations follow.A ring is a set R equipped with two binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s + : R × R → R and · : R × R → R (where × denotes the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
), called addition and multiplication. To qualify as a ring, the set and two operations, (R, +, · ), must satisfy the following requirements known as the ring axioms.
- (R, +) is required to be an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition:
| 1. | Closure under addition. | For all a, b in R, the result of the operation a + b is also in R. |
| 2. | Associativity of addition. | For all a, b, c in R, the equation (a + b) + c = a + (b + c) holds. |
| 3. | Existence of additive identity. | There exists an element 0 in R, such that for all elements a in R, the equation 0 + a = a + 0 = a holds. |
| 4. | Existence of additive inverse. | For each a in R, there exists an element b in R such that a + b = b + a = 0 |
| 5. | Commutativity of addition. | For all a, b in R, the equation a + b = b + a holds. |
- (R, ·) is required to be a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under multiplication:
| 1. | Closure under multiplication. | For all a, b in R, the result of the operation a · b is also in R. |
| 2. | Associativity of multiplication. | For all a, b, c in R, the equation (a · b) · c = a · (b · c) holds. |
| 3. | Existence of multiplicative identity. | There exists an element 1 in R, such that for all elements a in R, the equation 1 · a = a · 1 = a holds. |
- The distributive laws:
| 1. For all a, b and c in R, the equation a · (b + c) = (a · b) + (a · c) holds. |
| 2. For all a, b and c in R, the equation (a + b) · c = (a · c) + (b · c) holds. |
This definition assumes that a binary operation on R is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined on R×R with values in R. Therefore, for any a and b in R, the addition a + b and the product a · b are elements of R.
The most familiar example of a ring is the set of all integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, Z = {..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ... }, together with the usual operations of addition and multiplication.
Another familiar example is the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R, equipped with the usual addition and multiplication.
Another example of a ring is the set of all square matrices of a fixed size, with real elements, using the matrix addition and multiplication of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. In this case, the ring elements 0 and 1 are the zero matrix (with all entries equal to 0) and the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, respectively.
Second example: the ring Z4
Consider the set Z4 consisting of the numbers 0, 1, 2, 3 where addition and multiplication are defined as follows (note that for any integer x, x modModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
4 is defined to be the remainder when x is divided by 4):
- For any x, y in Z4, x + y is defined to be their sum in Z (the set of all integers) mod 4Modular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. So we can represent the additive structure of Z4 by the left-most table as shown.
- For any x, y in Z4, x ⋅ y is defined to be their product in Z (the set of all integers) mod 4. So we can represent the multiplicative structure of Z4 by the right-most table as shown.
| · | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | 0 | 2 | 0 | 2 |
| 3 | 0 | 3 | 2 | 1 |
| + | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
It is simple (but tedious) to verify that Z4 is a ring under these operations. First of all, one can use the left-most table to show that Z4 is closed under addition (any result is either 0, 1, 2 or 3). Associativity of addition in Z4 follows from associativity of addition in the set of all integers. The additive identity is 0 as can be verified by looking at the left-most table. Given an integer x, there is always an inverse of x; this inverse is given by 4 - x as one can verify from the additive table. Therefore, Z4 is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition.
Similarly, Z4 is closed under multiplication as the right-most table shows (any result above is either 0, 1, 2 or 3). Associativity of multiplication in Z4 follows from associativity of multiplication in the set of all integers. The multiplicative identity is 1 as can be verified by looking at the right-most table. Therefore, Z4 is a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under multiplication.
Distributivity of the two operations over each other follow from distributivity of addition over multiplication (and vice-versa) in Z (the set of all integers).
Therefore, this set does indeed form a ring under the given operations of addition and multiplication.
Properties of this ring
- In general, given any two integers, x and y, if x ⋅ y = 0, then either x is 0 or y is 0. It is interesting to note that this does not hold for the ring (Z4, +, ⋅):
-
- 2 ⋅ 2 = 0
- although neither factorFactorizationIn mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
is 0. In general, a non-zero element a of a ring, (R, +, ⋅) is said to be a zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
in (R, +, ⋅), if there exists a non-zero element b of R such that a ⋅ b = 0. So in this ring, the only zero divisor is 2 (note that 0 ⋅ a = 0 for any a in a ring (R, +, ⋅) so 0 is not considered to be a zero divisor).
- A commutative ring which has no zero divisors is called an integral domain (see below). So Z, the ring of all integers (see above), is an integral domain (and therefore a ring), although Z4 (the above example) does not form an integral domain (but is still a ring). So in general, every integral domain is a ring but not every ring is an integral domain.
Third example: the trivial ring
If we define on the singleton set {0}:0 + 0 = 0
0 × 0 = 0
then one can verify that ({0}, +, ×) forms a ring known as the trivial ring. Since there can be only one result for any product or sum (0), this ring is both closed and associative for addition and multiplication, and furthermore satisfies the distributive law. The additive and multiplicative identities are both equal to 0. Similarly, the additive inverse of 0 is 0. The trivial ring is also a (rather trivial) example of a zero ring
Zero ring
In ring theory, a branch of mathematics, a zero ring is a ring in which the product of any two elements is 0 . In ring theory, a branch of mathematics, a zero ring is a ring (without unity) in which the product of any two elements is 0 (the additive identity element). In ring theory, a branch of...
(see below).
Subring
Informally, a subringSubring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of a ring is another ring that uses the "same" operations and is contained in it. More formally, suppose (R, +, ·) is a ring, and S is a subset of R such that
- for every a, b in S, a + b is in S;
- for every a, b in S, a · b is in S;
- for every a in S, the additive inverse −a of a is in S; and
- the multiplicative identity '1' of R is in S.
Let '+S' and '·S' denote the operations '+' and '·', restricted to S×S. Then (S, +S, ·S) is a subring of (R, +, ·). Since the restricted operations are completely determined by S and the original ones, the subring is often written simply as (S, +, ·).
For example, a subring of the complex number ring C is any subset of C that includes 1 and is closed under addition, multiplication, and negation, such as:
- The rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q - The algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s A - The real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R
If A is a subring of R, and B is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of A such that B is also a subring of R, then B is a subring of A.
Homomorphism
A homomorphismRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
from a ring (R, +, ·) to a ring (S, ‡, *) is a function f from R to S that commutes with the ring operations; namely, such that, for all a, b in R the following identities hold:
- f(a + b) = f(a) ‡ f(b)
- f(a · b) = f(a) * f(b)
Moreover, the function f must take the identity element 1R of '·' to the identity element 1S of '*'.
(this is not required if identity is not required).
For example, the function that maps each integer x to its remainder modulo 4 (a number in {0, 1, 2, 3}) is a homomorphism from the ring Z to the ring Z4.
A ring homomorphism is said to be an isomorphism if there exists an inverse homomorphism to f (i.e., a ring homomorphism which is an inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
). Equivalently, any bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
ring homomorphism is a ring isomorphism.
Ideal
The purpose of an idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in a ring is to somehow allow one to define the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of a ring (analogous to the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
; see below). An ideal in a ring can therefore be thought of as a generalization of a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
in a group. More formally, let (R, +, · ) be a ring. A subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
I of R is said to be a right ideal in R if:
- (I, +) is a subgroup of the underlying additive group in (R, +, · ) (i.e. (I, +) is a subgroup of (R, +)).
- For every x in I and r in R, x · r is in I.
A left ideal is similarly defined with the second condition being replaced. More specifically, a subset I of R is a left ideal in R if:
- (I, +) is a subgroup of the underlying additive group in (R, +, · ) (i.e. (I, +) is a subgroup of (R, +)).
- For every x in I and r in R, r · x is in I.
Notes
- If k is in R, then the set of elements k · R is a right ideal in R, and the set of elements R · k is a left ideal in R. These ideals (for any k in R) are called the principalPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
right and left ideals generated by k.
- If every ideal in a ring (R, +, · ) is a principal ideal in (R, +, · ), (R, +, · ) is said to be a principal ideal ringPrincipal ideal ringIn mathematics, a principal right ideal ring is a ring R in which every right ideal is of the form xR for some element x of R...
.
- An ideal in a ring, (R, +, · ), is said to be a two-sided ideal if it is both a left ideal and right ideal in (R, +, · ). It is preferred to call a two-sided ideal, simply an ideal.
- If I = {0} (where 0 is the additive identity of the ring (R, +, · )), then I is an ideal known as the trivial ideal. Similarly, R is also an ideal in (R, +, · ) called the unit ideal.
Examples
- Any additive subgroup of the integers is an ideal in the integers with its natural ring structure.
- There are no non-trivial ideals in R (the ring of all real numbers) (i.e., the only ideals in R are {0} and R itself). More generally, a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
cannot contain any non-trivial ideals.
- From the previous example, every field must be a principal ideal ring.
- A subset, I, of a commutative ring (R, +, · ) is a left ideal if and only ifIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
it is a right ideal. So for simplicity's sake, we refer to any ideal in a commutative ring as just an ideal.
History
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s and the theory of algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s. Furthermore, the appearance of hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
s in the mid-19th century undercut the pre-eminence of fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
in mathematical analysis.
In the 1880s Richard Dedekind introduced the concept of a ring, and the term ring (Zahlring) was coined by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
in 1892 and published in the article Die Theorie der algebraischen Zahlkörper, Jahresbericht der Deutschen Mathematiker Vereinigung, Vol. 4, 1897. According to Harvey Cohn, Hilbert used the term for a specific ring that had the property of "circling directly back" to an element of itself.
The first axiomatic definition of a ring was given by Adolf Fraenkel in an essay in Journal für die reine und angewandte Mathematik (A. L. Crelle), vol. 145, 1914. In 1921, Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
gave the first axiomatic foundation of the theory of commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s in her monumental paper Ideal Theory in Rings.
Elementary properties of rings
Some properties of rings follow directly from the ring axioms through very simple proofsProofs of elementary ring properties
The following proofs of elementary ring properties use only the axioms that define a mathematical ring:-Multiplication by zero:Theorem: 0 ⋅ a = a ⋅ 0 = 0-Trivial ring:...
.
In particular, since the axioms state that (R,+) is a commutative group, all pertinent theorems of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
apply, such as the uniqueness of the additive identity and the uniqueness of the additive inverse of a particular element. In the same way one can prove the uniqueness of the inverse of a unit in a ring
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
.
However, rings also have specific properties that combine addition with multiplication. In any ring (R, +, ⋅):
- For any element a, the equations a ⋅ 0 = 0 ⋅ a = 0 hold.
- If 0 = 1, the ring is trivial (that is, R has only one element).
- For any element a, the equation (−1) ⋅ a = −a holds.
- For any elements a and b, the equations (−a) ⋅ b = a ⋅ (−b) = −(a ⋅ b) hold.
Quotient ring
Informally, the quotient ringQuotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of a ring, is a generalization of the notion of a quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of a group. More formally, given a ring (R, +, · ) and a two-sided ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
I of (R, +, · ), the quotient ring (or factor ring) R/I is the set of cosets of I (with respect to the underlying additive group of (R, +, · ); i.e. cosets with respect to (R, +)) together with the operations:
+ (b + I) = (a + b) + I and(b + I) = (ab) + I.
For every a, b in R.
Polynomial ring
Formal definitionLet (R, +R, ·R) be a ring and let
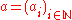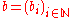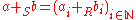
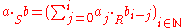
where the convention that is the set of all nonnegative integers, is adopted. Define +S : S × S → S and ·S : S × S → S, as follows (where and are arbitrary elements of S):Then (S, +S, ·S) is a ring referred to as the polynomial ring over R.
Notes
Most authors write S as R[X], where
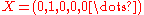is an element of S. This convention is adopted because if 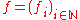is an element of S, and if 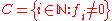, f can be written as a polynomial with coefficients in R, in the variable X, as follows: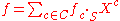This allows one to view S as merely the set of all polynomials over R in the variable X, with multiplication and addition of polynomials defined in the canonical manner. Therefore, in all that follows, S, denoted by R[X], shall be identified in this fashion. Addition and multiplication in S, and those of the underlying ring R, will be denoted by juxtaposition.
Matrix ring
Formal definitionLet (R, +R, ·R) be a ring and let
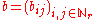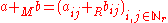
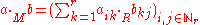
. Define +M : Mr(R) × Mr(R) → Mr(R) and ·M : Mr(R) × Mr(R) → Mr(R), as follows (where and are arbitrary elements of Mr(R)):Then (Mr(R), +M, ·M) is a ring referred to as the ring of r×r matrices over R.
Notes
The ring Mr(R) can be viewed as merely the ring of r×r matrices over R with matrix addition and multiplication defined in the canonical manner. For given
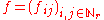in Mr(R), f can be identified with the r×r matrix whose (i, j)-entry is . Therefore, in all that follows, Mr(R) and each of its elements shall be identified in this fashion. Addition and multiplication in Mr(R), and those of the underlying ring R, will be denoted by juxtaposition.Some examples of the ubiquity of rings
Many different kinds of mathematical objectMathematical object
In mathematics and the philosophy of mathematics, a mathematical object is an abstract object arising in mathematics.Commonly encountered mathematical objects include numbers, permutations, partitions, matrices, sets, functions, and relations...
s can be fruitfully analyzed in terms of some associated ring
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
.
Cohomology ring of a topological space
To any topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X one can associate its integral cohomology ring
Cohomology ring
In mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
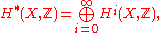
a graded ring. There are also homology groups
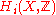of a space, and indeed these were defined first, as a useful tool for distinguishing between certain pairs of topological spaces, like the sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s and tori
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, for which the methods of point-set topology are not well-suited. Cohomology groups were later defined in terms of homology groups in a way which is roughly analogous to the dual of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. To know each individual integral homology group is essentially the same as knowing each individual integral cohomology group, because of the universal coefficient theorem
Universal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
. However, the advantage of the cohomology groups is that there is a natural product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
, which is analogous to the observation that one can multiply pointwise a k-multilinear form and an l-multilinear form to get a (k + l)-mulilinear form.
The ring structure in cohomology provides the foundation for characteristic class
Characteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es of fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s, intersection theory on manifolds and algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, Schubert calculus
Schubert calculus
In mathematics, Schubert calculus is a branch of algebraic geometry introduced in the nineteenth century by Hermann Schubert, in order to solve various counting problems of projective geometry...
and much more.
Burnside ring of a group
To any groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is associated its Burnside ring
Burnside ring
In mathematics, the Burnside ring of a finite group is an algebraic construction that encodes the different ways the group can act on finite sets...
which uses a ring to describe the various ways the group can act
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a finite set. The Burnside ring's additive group is the free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
whose basis are the transitive actions of the group and whose addition is the disjoint union of the action. Expressing an action in terms of the basis is decomposing an action into its transitive constituents. The multiplication is easily expressed in terms of the representation ring
Representation ring
In mathematics, especially in the area of algebra known as representation theory, the representation ring of a group is a ring formed from all the linear representations of the group. For a given group, the ring will depend on the base field of the representations...
: the multiplication in the Burnside ring is formed by writing the tensor product of two permutation modules as a permutation module. The ring structure allows a formal way of subtracting one action from another. Since the Burnside ring is contained as a finite index subring of the representation ring, one can pass easily from one to the other by extending the coefficients from integers to the rational numbers.
Representation ring of a group ring
To any group ringGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
or Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
is associated its representation ring
Representation ring
In mathematics, especially in the area of algebra known as representation theory, the representation ring of a group is a ring formed from all the linear representations of the group. For a given group, the ring will depend on the base field of the representations...
or "Green ring". The representation ring's additive group is the free abelian group whose basis are the indecomposable modules and whose addition corresponds to the direct sum. Expressing a module in terms of the basis is finding an indecomposable decomposition of the module. The multiplication is the tensor product. When the algebra is semisimple, the representation ring is just the character ring from character theory
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
, which is more or less the Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
given a ring structure.
Function field of an irreducible algebraic variety
To any irreducible algebraic varietyAlgebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
is associated its function field
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
. The points of an algebraic variety correspond to valuation ring
Valuation ring
In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
s contained in the function field and containing the coordinate ring. The study of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
makes heavy use of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
to study geometric concepts in terms of ring-theoretic properties. Birational geometry
Birational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
studies maps between the subrings of the function field.
Face ring of a simplicial complex
Every simplicial complexSimplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
has an associated face ring, also called its Stanley–Reisner ring. This ring reflects many of the combinatorial properties of the simplicial complex, so it is of particular interest in algebraic combinatorics
Algebraic combinatorics
Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
. In particular, the algebraic geometry of the Stanley–Reisner ring was used to characterize the numbers of faces in each dimension of simplicial polytope
Simplicial polytope
In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
s.
Finite ring
Given a natural number m, how many distinct rings (not necessarily with unity) have m elements? When m is prime there are only two rings of order m; the additive group of each being isomorphic to the cyclic group of order m. One is the zero ringZero ring
In ring theory, a branch of mathematics, a zero ring is a ring in which the product of any two elements is 0 . In ring theory, a branch of mathematics, a zero ring is a ring (without unity) in which the product of any two elements is 0 (the additive identity element). In ring theory, a branch of...
and the other is the Galois field.
As with finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, the complexity of the classification depends upon the complexity of the prime factorization of m. If m is the square of a prime, for instance, there are precisely eleven rings having order m. On the other hand, there can be only two groups having order m; both of which are abelian.
The theory of finite rings is more complex than that of finite abelian groups, since any finite abelian group is the additive group of at least two nonisomorphic finite rings: the direct product of copies of
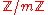, and the zero ring. On the other hand, the theory of finite rings is simpler than that of not necessarily abelian finite groups. For instance, the classification of finite simple groupsClassification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
was one of the major breakthroughs of 20th century mathematics, its proof spanning thousands of journal pages. On the other hand, any finite simple ring
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
is isomorphic to the ring
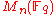of n by n matrices over a finite field of order q. This follows from two theorems of Joseph WedderburnJoseph Wedderburn
Joseph Henry Maclagan Wedderburn was a Scottish mathematician, who taught at Princeton University for most of his career. A significant algebraist, he proved that a finite division algebra is a field, and part of the Artin–Wedderburn theorem on simple algebras...
established in 1905 and 1907.
One of these theorems, known as Wedderburn's little theorem
Wedderburn's little theorem
In mathematics, Wedderburn's little theorem states that every finite domain is a field. In other words, for finite rings, there is no distinction between domains, skew-fields and fields.The Artin–Zorn theorem generalizes the theorem to alternative rings....
, asserts that any finite division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
is necessarily commutative. Nathan Jacobson
Nathan Jacobson
Nathan Jacobson was an American mathematician....
later discovered yet another condition which guarantees commutativity of a ring:
If for every element r of R there exists an integer such that , then R is commutative.
If, r2 = r for every r, the ring is called a Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
. More general conditions which guarantee commutativity of a ring are also known.
The number of rings with m elements, for m a natural number, is listed under A027623 in the On-Line Encyclopedia of Integer Sequences
On-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
.
Associative algebras
An associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
is a ring that is also a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field K. For instance, the set of n by n matrices over the real field R has dimension n2 as a real vector space, and the matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
corresponds to the ring multiplication. For a non-trivial but elementary example consider 2 × 2 real matrices.
Lie ring
A Lie ringLie ring
In mathematics a Lie ring is a structure related to Lie algebras that can arise as a generalisation of Lie algebras, or through the study of the lower central series of groups.- Formal definition :...
is defined to be a ring that is nonassociative
Nonassociative ring
In abstract algebra, a nonassociative ring is a generalization of the concept of ring.A nonassociative ring is a set R with two operations, addition and multiplication, such that:# R is an abelian group under addition:## a+b = b+a...
and anticommutative under multiplication, that also satisfies the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. More specifically we can define a Lie ring
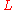to be an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition with an operation
that has the following properties:- Bilinearity:
- for all x, y, z ∈ L.
- Jacobi identity:
- for all x, y, z in L.
- For all x in L.
Lie rings need not be Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s under addition. Any Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is an example of a Lie ring. Any associative ring can be made into a Lie ring by defining a bracket operator
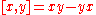. Conversely to any Lie algebra there is a corresponding ring, called the universal enveloping algebraUniversal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
.
Lie rings are used in the study of finite p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
s through the Lazard correspondence. The lower central factors of a p-group are finite abelian p-groups, so modules over Z/pZ. The direct sum of the lower central factors is given the structure of a Lie ring by defining the bracket to be the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of two coset representatives. The Lie ring structure is enriched with another module homomorphism, then pth power map, making the associated Lie ring a so-called restricted Lie ring.
Lie rings are also useful in the definition of a p-adic analytic groups and their endomorphisms by studying Lie algebras over rings of integers such as the p-adic integers. The definition of finite groups of Lie type due to Chevalley involves restricting from a Lie algebra over the complex numbers to a Lie algebra over the integers, and the reducing modulo p to get a Lie algebra over a finite field.
Topological ring
Let (X, T) is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and (X, +, · ) be a ring. Then (X, T, +, · ) is said to be a topological ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
, if its ring structure and topological structure are both compatible (i.e work together) over each other. That is, the addition map (
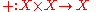) and the multiplication map ( 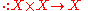) have to be both continuous as maps between topological spaces where X x X inherits the product topologyProduct topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
. So clearly, any topological ring is a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
(under addition).
Examples
- The set of all real numbers, R, with its natural ring structure and the standard topology forms a topological ring.
- The direct product of two topological rings is also a topological ring.
Commutative rings
Although ring addition is commutative, so that for every a, b in R, a + b = b + a, ring multiplication is not required to be commutative; a · b need not equal b · a for all a, b in R. Rings that also satisfy commutativity for multiplication are called commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s. Formally,
Formal definition
Let (R, +, · ) be a ring. Then (R, +, · ) is said to be a commutative ring if for every a, b in R, a · b = b · a. That is, (R, +, · ) is required to be a commutative monoid under multiplication.
Examples
- The integers form a commutative ring under the natural operations of addition and multiplication.
- An example of a noncommutative ring is the ring of n × n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over a non-trivial fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, for n > 1. In particular, the ring of all 2 × 2 matrices over R (the set of all real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s) do not form a commutative ring as the following computationComputationComputation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
shows:
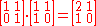, which is not equal to Principal ideal domains
Although rings are structurally similar to the integers, there are certain ring-theoretic properties that the integers may satisfy but a general ring may not. One such property is the requirement that every ideal in a ring be generated by a single element; that is, be a principal ideal. Formally,Definition
Let R be a ring. Then R is said to be a principal ideal ring (abbreviated PIR), if every ideal in R is of the form a · R = {a · r | r in R}. A principal ideal domain (PID) is a principal ideal ring that is also an integral domain.
The requirement that a ring be a principal ideal domain is somewhat stronger than the other more common properties a ring may satisfy. For example, it is true that if a ring, R, is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
(UFD), then the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over R is also a UFD. However, such a result does not in general hold for principal ideal rings. For example, the integers are an easy example of a principal ideal ring, but the polynomial ring over the integers fails to be a PIR; if R = Z[x] denotes the polynomial ring over the integers, I = 2 · R + X · R is an ideal which cannot be generated by a single element. Despite this counterexample, the polynomial ring over any field is always a principal ideal domain and in fact, a Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
. More generally, a polynomial ring is a PID if and only if the polynomial ring in question is over a field.
Aside from the polynomial ring over a PIR, principal ideal rings possess many interesting properties due to their connection with the integers in terms of divisibility; that is, principal ideal domains behave similarly to the integers with respect to divisibility. For example, any PID is a UFD; i.e., an analogue of the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
holds for principal ideal domains. Furthermore, since Noetherian rings are precisely those rings in which any ideal is finitely generated, principal ideal domains are trivially Noetherian rings. The fact that irreducible elements coincide with prime elements for PID's, together with the fact that every PID is Noetherian, implies that any PID is a UFD. One can also speak of the greatest common divisor of two elements in a PID; if x and y are elements of R, a principal ideal domain, then x · R + y · R = c · R for some c in R since the left-hand side is indeed an ideal. Therefore, c is the desired "GCD" of x and y.
An important class of rings lying in between fields and PID's, is the class of Euclidean domains. In particular, any field is a Euclidean domain, and any Euclidean domain is a PID. An ideal in a Euclidean domain is generated by any element of that ideal with minimum degree (all such elements must be associate). However, not every PID is a Euclidean domain; the ring
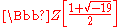furnishes a counterexample.Unique factorization domains
The theory of unique factorization domains (UFD) also forms an important part of ring theory. In effect, a unique factorization domain is ring in which an analogue of the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
holds. Formally,
Definition
Let R be a ring. Then R is said to be a unique factorization domain (abbreviated UFD), if the following conditions are satisfied:
1. R is an integral domain.
2. Every non-zero non-unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
of R is the product of a finite number of irreducible elements.
3. If
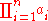= , where all ai's and bj's are irreducible, then n = m and after possible renumbering of the ai's and bj's, bi = ai · ui where ui is a unitUnit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in R.
The second condition above guarantees that "non-trivial" elements of R can be decomposed into irreducibles, and according to the third condition, such a finite decomposition is unique "up to multiplication by unit elements." This weakened form of uniqueness is reasonable to assume for otherwise even the integers would not satisfy the properties of being a UFD ((-2)2 = 22 = 4 demonstrates two "distinct" decompositions of 4; however both decompositions of 4 are equivalent up to multiplication by units (-1 and +1)). The fact that the integers constitute a UFD follows from the fundamental theorem of arithmetic.
For arbitrary rings, one may define a prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
and an irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
; these two may not in general coincide. However, a prime element in a domain is always irreducible. For UFD's, irreducible elements are also primes.
The class of unique factorization domains is related to other classes of rings. For instance, any Noetherian domain
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
satisfies conditions 1 and 2 above, but in general Noetherian domains fail to satisfy condition 3. However, if the set of prime elements and the set of irreducible elements coincide for a Noetherian domain, the third condition of a UFD is satisfied. In particular, principal ideal domains are UFD's.
Integral domains and fields
While rings are very important mathematical objects, there are a lot of restrictions involved in their theory. For instance, suppose we have a ring R and suppose a and b are in R. If a is non-zero and a · b = 0, then b need not necessarily be 0. In particular, if a · b = a · c with a non-zero b need not equal c. An example of this is the set of n x n matrices over R where a maybe such a non-zero matrix but may be singular. In this case, the result may not be true. However, we can impose additional conditions on the ring to ensure that this be true; namely make the ring into an integral domain (that is a non-trivial commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with no zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s). But we still run into a problem; namely we can't necessarily divide by non-zero elements. For example, the collection of all integers form an integral domain but we still can't divide an integer a by another integer b. For example, 2 cannot divide 3 to obtain another element in this ring. However, this problem can readily be solved if we ensure that every element in the ring has a multiplicative inverse. A field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is a ring in which the non-zero elements form an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under multiplication. In particular, a field is an integral domain (and therefore has no zero divisors) along with an additional operation of 'division'. Namely, if a and b are in a field F, then a/b is defined to be a · b−1 which is well defined.
Formal definition
Let (R, +, · ) be a ring. Then (R, +, · ) is said to be an integral domain if (R, +, · ) is commutative and has no zero divisors. Furthermore, (R, +, · ) is said to be a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, if its non-zero elements form an abelian group under multiplication.
Note
- If we require that the zero element (0) in a ring to have a multiplicative inverse, then the ring must be trivial.
Examples
- The integers form a commutative ring under the natural operations of addition and multiplication. In fact, the integers form what is known as an integral domain (a commutative ring with no zero divisors).
- A ring whose non-zero elements form an abelian group under multiplication (not just a commutative monoid), is called a field. So every field is an integral domain and every integral domain is a commutative ring. Furthermore, any finite integral domain is a field.
Relation to other algebraic structures
The following is a chain of class inclusions that describes the relationship between rings, domains and fields:- Commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s ⊃ integral domains ⊃ half factorization domains ⊃unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s ⊃ principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
s ⊃ Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
s ⊃ fieldsField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
Fields and integral domains are very important in modern algebra.
Noncommutative rings
The study of noncommutative ringNoncommutative ring
In mathematics, more specifically modern algebra and ring theory, a noncommutative ring is a ring whose multiplication is not commutative; that is, if R is a noncommutative ring, there exists a and b in R with a·b ≠ b·a, and conversely.Noncommutative rings are ubiquitous in mathematics, and occur...
s is a major area in modern algebra; especially ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
. Often noncommutative rings possess interesting invariants that commutative rings do not. As an example, there exist rings which contain non-trivial proper left or right ideals, but are still simple
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
; that is contain no non-trivial proper (two-sided) ideals. This example illustrates how one must take care when studying noncommutative rings because of possible counterintuitive misconceptions.
The theory of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s is one illustration of a special case of an object studied in noncommutative ring theory. In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the "scalars of a vector space" are required to lie in a field - a commutative division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
. The concept of a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, however, requires only that the scalars lie in an abstract ring. Neither commutativity nor the division ring assumption is required on the scalars in this case. Module theory has various applications in noncommutative ring theory, as one can often obtain information about the structure of a ring by making use of its modules. The concept of the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of a ring; that is, the intersection of all right/left annihilators
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of simple
Simple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
right/left modules over a ring, is one example. The fact that the Jacobson radical can be viewed as the intersection of all maximal right/left ideals in the ring, shows how the internal structure of the ring is reflected by its modules. It is also remarkable that the intersection of all maximal right ideals in a ring is the same as the intersection of all maximal left ideals in the ring, in the context of all rings; whether commutative or noncommutative. Therefore, the Jacobson radical also captures a concept which may seem to be not well-defined for noncommutative rings.
Noncommutative rings serve as an active area of research due to their ubiquity in mathematics. For instance, the ring of n by n matrices over a field
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is noncommutative despite its natural occurrence in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. More generally, endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
s of abelian groups are rarely commutative.
Noncommutative rings, like noncommutative groups, are not very well understood. For instance, although every finite abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
is the direct sum of (finite) cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of prime-power order, non-abelian groups do not possess such a simple structure. Likewise, various invariants exist for commutative rings, whereas invariants of noncommutative rings are difficult to find. As an example, the nilradical, although "innocent" in nature, need not be an ideal unless the ring is assumed to be commutative. Specifically, the set of all nilpotent elements in the ring of all n x n matrices over a division ring never forms an ideal, irrespective of the division ring chosen. Therefore, the nilradical cannot be studied in noncommutative ring theory. Note however that there are analogues of the nilradical defined for noncommutative rings, that coincide with the nilradical when commutativity is assumed.
One of the best known noncommutative rings is the division ring of quaternions.
Category theoretical description
Every ring can be thought of as a monoidMonoid (category theory)
In category theory, a monoid in a monoidal category is an object M together with two morphisms* \mu : M\otimes M\to M called multiplication,* and \eta : I\to M called unit,...
in Ab, the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
(thought of as a monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
under the tensor product of
-modules). The monoid action of a ring R on a abelian group is simply an R-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. Essentially, an R-module is a generalization of the notion of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
- where rather than a vector space over a field, one has a "vector space over a ring".
Let (A, +) be an abelian group and let End(A) be its endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
(see above). Note that, essentially, End(A) is the set of all morphisms of A, where if f is in End(A), and g is in End(A), the following rules may be used to compute f + g and f · g:
- (f + g)(x) = f(x) + g(x)
- (f · g)(x) = f(g(x))
where + as in f(x) + g(x) is addition in A, and function composition is denoted from right to left. Therefore, associated
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
to any abelian group, is a ring. Conversely, given any ring, (R, +, · ), (R, +) is an abelian group. Furthermore, for every r in R, right (or left) multiplication by r gives rise to a morphism of (R, +), by right (or left) distributivity. Let A = (R, +). Consider those endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of A, that "factor through" right (or left) multiplication of R. In other words, let EndR(A) be the set of all morphisms m of A, having the property that m(r · x) = r · m(x). It was seen that every r in R gives rise to a morphism of A - right multiplication by r. It is in fact true that this association of any element of R, to a morphism of A, as a function from R to EndR(A), is an isomorphism of rings. In this sense, therefore, any ring can be viewed as the endomorphism ring of some abelian X-group (by X-group, it is meant a group with X being its set of operators
Group with operators
In abstract algebra, a branch of pure mathematics, the algebraic structure group with operators or Ω-group is a group with a set of group endomorphisms.Groups with operators were extensively studied by Emmy Noether and her school in the 1920s...
). In essence, the most general form of a ring, is the endomorphism group of some abelian X-group.
General references
- Atiyah M. F.Michael AtiyahSir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
, Macdonald, I. G.Ian G. MacdonaldIan Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
, Introduction to commutative algebra. Addison-Wesley Publishing Co., Reading, Mass.-London-Don Mills, Ont. 1969 ix+128 pp. - Beachy, J. A. Introductory Lectures on Rings and Modules. Cambridge, England: Cambridge University Press, 1999.
- Dresden, G. "Small Rings." http://home.wlu.edu/~dresdeng/smallrings/
- Ellis, G. Rings and Fields. Oxford, England: Oxford University Press, 1993.
- Goodearl, K. R., Warfield, R. B., Jr., An introduction to noncommutative Noetherian rings. London Mathematical Society Student Texts, 16. Cambridge University Press, Cambridge, 1989. xviii+303 pp. ISBN 0-521-36086-2
- Herstein, I. N., Noncommutative rings. Reprint of the 1968 original. With an afterword by Lance W. Small. Carus Mathematical Monographs, 15. Mathematical Association of America, Washington, DC, 1994. xii+202 pp. ISBN 0-88385-015-X
- Nagell, T. "Moduls, Rings, and Fields." §6 in Introduction to Number Theory. New York: Wiley, pp. 19–21, 1951
- Nathan JacobsonNathan JacobsonNathan Jacobson was an American mathematician....
, Structure of rings. American Mathematical Society Colloquium Publications, Vol. 37. Revised edition American Mathematical Society, Providence, R.I. 1964 ix+299 pp. - Nathan Jacobson, The Theory of Rings. American Mathematical Society Mathematical Surveys, vol. I. American Mathematical Society, New York, 1943. vi+150 pp.
- Lam, T. Y., A first course in noncommutative rings. Second edition. Graduate Texts in Mathematics, 131. Springer-Verlag, New York, 2001. xx+385 pp. ISBN 0-387-95183-0
- Lam, T. Y., Exercises in classical ring theory. Second edition. Problem Books in Mathematics. Springer-Verlag, New York, 2003. xx+359 pp. ISBN 0-387-00500-5
- Lam, T. Y., Lectures on modules and rings. Graduate Texts in Mathematics, 189. Springer-Verlag, New York, 1999. xxiv+557 pp. ISBN 0-387-98428-3.
- McConnell, J. C.; Robson, J. C. Noncommutative Noetherian rings. Revised edition. Graduate Studies in Mathematics, 30. American Mathematical Society, Providence, RI, 2001. xx+636 pp. ISBN 0-8218-2169-5
- Rowen, Louis H., Ring theory. Vol. I, II. Pure and Applied Mathematics, 127, 128. Academic Press, Inc., Boston, MA, 1988. ISBN 0-12-599841-4, ISBN 0-12-599842-2
- Sloane, N. J. A. Sequences A027623 and A037234 in "The On-Line Encyclopedia of Integer Sequences
- Zwillinger, D. (Ed.). "Rings." §2.6.3 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 141–143, 1995
Special references
- Ballieu, R. "Anneaux finis; systèmes hypercomplexes de rang trois sur un corps commutatif." Ann. Soc. Sci. Bruxelles. Sér. I 61, 222-227, 1947.
- Berrick, A. J. and Keating, M. E. An Introduction to Rings and Modules with K-Theory in View. Cambridge, England: Cambridge University Press, 2000.
- Fine, B. "Classification of Finite Rings of Order ." Math. Mag. 66, 248-252, 1993
- Fletcher, C. R. "Rings of Small Order." Math. Gaz. 64, 9-22, 1980
- Fraenkel, A. "Über die Teiler der Null und die Zerlegung von Ringen." J. reine angew. Math. 145, 139-176, 1914
- Gilmer, R. and Mott, J. "Associative Rings of Order ." Proc. Japan Acad. 49, 795-799, 1973
- Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, 1998
- Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998
- Korn, G. A. and Korn, T. M. Mathematical Handbook for Scientists and Engineers. New York: Dover, 2000
- Pierce, Richard S., Associative algebras. Graduate Texts in Mathematics, 88. Studies in the History of Modern Science, 9. Springer-Verlag, New York–Berlin, 1982. xii+436 pp. ISBN 0-387-90693-2
Historical references
- History of ring theory at the MacTutor Archive
- Birkhoff, G. and Mac Lane, S. A Survey of Modern Algebra, 5th ed. New York: Macmillian, 1996
- Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 4th ed. New York: Springer-Verlag, 2004. ISBN 3-540-43491-7
- Faith, Carl, Rings and things and a fine array of twentieth century associative algebra. Mathematical Surveys and Monographs, 65. American Mathematical Society, Providence, RI, 1999. xxxiv+422 pp. ISBN 0-8218-0993-8
- Itô, K. (Ed.). "Rings." §368 in Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 2. Cambridge, MA: MIT Press, 1986
- Kleiner, I. "The Genesis of the Abstract Ring Concept." Amer. Math. Monthly 103, 417-424, 1996
- Renteln, P. and Dundes, A. "Foolproof: A Sampling of Mathematical Folk Humor." Notices Amer. Math. Soc. 52, 24-34, 2005
- Singmaster, D. and Bloom, D. M. "Problem E1648." Amer. Math. Monthly 71, 918-920, 1964
- Van der Waerden, B. L. A History of Algebra. New York: Springer-Verlag, 1985
- Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002