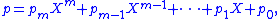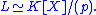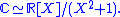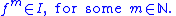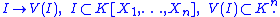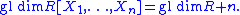Polynomial ring
Encyclopedia
In mathematics
, especially in the field of abstract algebra
, a polynomial ring is a ring
formed from the set of polynomial
s in one or more variables with coefficients in another ring
. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of splitting field
s, and to the understanding of a linear operator. Many important conjectures involving polynomial rings, such as Serre's problem
, have influenced the study of other rings, and have influenced even the definition of other rings, such as group ring
s and rings of formal power series
.
K is an expression of the form
where p0, …, pm are elements of K, the coefficients of p, and X, X 2, … are formal symbols ("the powers of X"). Such expressions can be added and multiplied, and then brought into the same form using the ordinary rules for manipulating algebraic expressions, such as associativity
, commutativity
, distributivity
, and collecting the similar terms. Any term pkX k with zero coefficient, pk = 0, may be omitted. The product of the powers of X is defined by the familiar formula
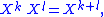
where k and l are any natural number
s. Two polynomials are considered to be equal if and only if the corresponding coefficients for each power of X are equal. By convention, X 1 = X, X 0 = 1, and the sum defining the polynomial p may be viewed as the linear combination
of the symbols X m, …, X 1, X 0 with coefficients pm, …, p1, p0. Using the summation
symbol, the same polynomial is expressed more compactly as follows:
The summation limits are frequently omitted, so that the same polynomial is written as
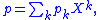
and it is understood that only finitely many terms are present, i.e. pk is zero for all large enough values of k, in our case, for k > m. The degree of a polynomial is the largest k such that the coefficient of X k is not zero. In the special case of zero polynomial, all of whose coefficients are zero, the degree is undefined, or sometimes defined to be the symbol −∞.
denoted K[X] and is called the ring of polynomials over K. The symbol X is commonly called the "variable", and this ring is also called the ring of polynomials in one variable over K, to distinguish it from more general rings of polynomials in several variables. This terminology is suggested by the important cases of polynomials with real
or complex
coefficients, which may be alternatively viewed as real or complex polynomial functions. However, in general, X and its powers, X k, are treated as formal symbols, not as elements of the field K. One can think of the ring K[X] as arising from K by adding one new element X that is external to K and requiring that X commute with all elements of K. In order for K[X] to form a ring, all powers of X have to be included as well, and this leads to the definition of polynomials as linear combinations of the powers of X with coefficients in K.
A ring has two binary operations, addition and multiplication. In the case of the polynomial ring K[X], these operations are explicitly given by the following formulas:
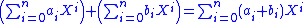
and
In the first formula, one of the polynomials may be extended by adding "dummy terms" with zero coefficients, so that the same set of powers formally appears in both summands. In the second formula, the inner summation in the right hand side is only extended over indices within bounds, 0 ≤ i ≤ m and 0 ≤ j ≤ n. Alternative forms of expressing addition and multiplication, without using explicit bounds in the sums, are as follows:
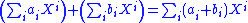
and
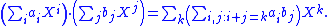
Since only finitely many coefficients ai and bj are non-zero, all sums in effect have only finitely many terms, and hence represent polynomials from K[X].
Since a polynomial from K[X] can be multiplied by a "scalar
" k from K to yield a new polynomial, K[X] actually constitute an associative algebra
over K. Viewed as a vector space, K[X] has a basis
consisting of the countably infinite set {1, X, X 2, X 3, ...}.
More generally, the field K can be replaced by any commutative ring
R, giving rise to the polynomial ring over R , which is denoted R[X].
s in many respects. This analogy and the arithmetic of the ring of polynomials were thoroughly investigated by Gauss and his theory served as a model for development of abstract algebra
in the second half of the nineteenth century in the works of Kummer
, Kronecker
, and Dedekind
.
noted that every positive integer can be uniquely factored into a product of primes
— this statement is now called the fundamental theorem of arithmetic
. The proof is based on Euclid's algorithm for finding the greatest common divisor
of natural number
s. At each step of this algorithm, a pair (a, b), a > b, of natural numbers is replaced by a new pair (b, r), where r is the remainder from the division of a by b, and the new numbers are smaller. Gauss remarked that the procedure of division with the remainder can also be defined for polynomials: given two polynomials p and q, where q ≠ 0, one can write
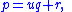
where the quotient u and the remainder r are polynomials, the degree of r is less than the degree of q, and a decomposition with these properties is unique. The quotient and the remainder are found using the polynomial long division
. The degree of the polynomial now plays a role similar to the absolute value of an integer: it is strictly less in the remainder r than it is in q, and when repeating this step such decrease cannot go on indefinitely. Therefore eventually some division will be exact, at which point the last non-zero remainder is the greatest common divisor of the initial two polynomials. Using the existence of greatest common divisors, Gauss was able to simultaneously rigorously prove the fundamental theorem of arithmetic for integers and its generalization to polynomials. In fact there exist other commutative rings than Z and K[X] that similarly admit an analogue of the Euclidean algorithm; all such rings are called Euclidean rings. Rings for which there exists unique (in an appropriate sense) factorization of nonzero elements into irreducible
factors are called unique factorization domain
s or factorial rings; the given construction shows that all Euclidean rings, and in particular Z and K[X], are unique factorization domains.
Another corollary of the polynomial division with the remainder is the fact that every proper ideal
I of K[X] is principal
, i.e. I consists of the multiples of a single polynomial f. Thus the polynomial ring K[X] is a principal ideal domain
, and for the same reason every Euclidean domain is a principal ideal domain. Also every principal ideal domain is a unique-factorization domain. These deductions make essential use of the fact that the polynomial coefficients lie in a field
, namely in the polynomial division step, which requires the leading coefficient of q, which is only known to be non-zero, to have an inverse. If R is an integral domain that is not a field then R[X] is neither a Euclidean domain nor a principal ideal domain; however it could still be a unique factorization domain (and will be so if and only it R itself is a unique factorization domain, for instance if it is Z or another polynomial ring).
s of K.
Suppose that a commutative ring L contains K and there exists an element θ of L such that the ring L is generated by θ over K. Thus any element of L is a linear combination of powers of θ with coefficients in K. Then there is a unique ring homomorphism
φ from K[X] into L which does not affect the elements of K itself (it is the identity map
on K) and maps each power of X to the same power of θ. Its effect on the general polynomial amounts to "replacing X with θ":
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the field of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a polynomial ring is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
formed from the set of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in one or more variables with coefficients in another ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
s, and to the understanding of a linear operator. Many important conjectures involving polynomial rings, such as Serre's problem
Quillen–Suslin theorem
The Quillen–Suslin theorem, also known as Serre's problem or Serre's conjecture, is a theorem in commutative algebra about the relationship between free modules and projective modules over polynomial rings...
, have influenced the study of other rings, and have influenced even the definition of other rings, such as group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
s and rings of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
.
Polynomials
A polynomial in X with coefficients in a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is an expression of the form
where p0, …, pm are elements of K, the coefficients of p, and X, X 2, … are formal symbols ("the powers of X"). Such expressions can be added and multiplied, and then brought into the same form using the ordinary rules for manipulating algebraic expressions, such as associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
, and collecting the similar terms. Any term pkX k with zero coefficient, pk = 0, may be omitted. The product of the powers of X is defined by the familiar formula
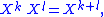
where k and l are any natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. Two polynomials are considered to be equal if and only if the corresponding coefficients for each power of X are equal. By convention, X 1 = X, X 0 = 1, and the sum defining the polynomial p may be viewed as the linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the symbols X m, …, X 1, X 0 with coefficients pm, …, p1, p0. Using the summation
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
symbol, the same polynomial is expressed more compactly as follows:
The summation limits are frequently omitted, so that the same polynomial is written as
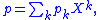
and it is understood that only finitely many terms are present, i.e. pk is zero for all large enough values of k, in our case, for k > m. The degree of a polynomial is the largest k such that the coefficient of X k is not zero. In the special case of zero polynomial, all of whose coefficients are zero, the degree is undefined, or sometimes defined to be the symbol −∞.
The polynomial ring K[X]
The set of all polynomials with coefficients in the field K forms a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
denoted K[X] and is called the ring of polynomials over K. The symbol X is commonly called the "variable", and this ring is also called the ring of polynomials in one variable over K, to distinguish it from more general rings of polynomials in several variables. This terminology is suggested by the important cases of polynomials with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
coefficients, which may be alternatively viewed as real or complex polynomial functions. However, in general, X and its powers, X k, are treated as formal symbols, not as elements of the field K. One can think of the ring K[X] as arising from K by adding one new element X that is external to K and requiring that X commute with all elements of K. In order for K[X] to form a ring, all powers of X have to be included as well, and this leads to the definition of polynomials as linear combinations of the powers of X with coefficients in K.
A ring has two binary operations, addition and multiplication. In the case of the polynomial ring K[X], these operations are explicitly given by the following formulas:
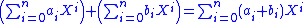
and
In the first formula, one of the polynomials may be extended by adding "dummy terms" with zero coefficients, so that the same set of powers formally appears in both summands. In the second formula, the inner summation in the right hand side is only extended over indices within bounds, 0 ≤ i ≤ m and 0 ≤ j ≤ n. Alternative forms of expressing addition and multiplication, without using explicit bounds in the sums, are as follows:
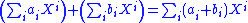
and
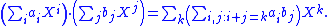
Since only finitely many coefficients ai and bj are non-zero, all sums in effect have only finitely many terms, and hence represent polynomials from K[X].
Since a polynomial from K[X] can be multiplied by a "scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
" k from K to yield a new polynomial, K[X] actually constitute an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over K. Viewed as a vector space, K[X] has a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
consisting of the countably infinite set {1, X, X 2, X 3, ...}.
More generally, the field K can be replaced by any commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R, giving rise to the polynomial ring over R , which is denoted R[X].
Properties of K[X]
The polynomial ring K[X] is remarkably similar to the ring Z of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s in many respects. This analogy and the arithmetic of the ring of polynomials were thoroughly investigated by Gauss and his theory served as a model for development of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
in the second half of the nineteenth century in the works of Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
, Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
, and Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
.
K[X] is an integral domain
The first property of the polynomial ring is elementary and says that a product of two non-zero polynomials is also a non-zero polynomial. Indeed, the product of a polynomial p of degree m starting with pmX m, pm ≠ 0, and a polynomial q of degree n starting with qnX n, qn ≠ 0, is the polynomial pq starting with the term rX m+n, where the coefficient r = pmqn ≠ 0. Hence pq is a non-zero polynomial of degree m + n. Commutative rings with unity e=x0 in which the product of any two non-zero elements is non-zero are called integral domains, and thus the polynomial ring K[X] is an integral domain.Factorization in K[X]
The next property of the polynomial ring is much deeper. Already EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
noted that every positive integer can be uniquely factored into a product of primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
— this statement is now called the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. The proof is based on Euclid's algorithm for finding the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. At each step of this algorithm, a pair (a, b), a > b, of natural numbers is replaced by a new pair (b, r), where r is the remainder from the division of a by b, and the new numbers are smaller. Gauss remarked that the procedure of division with the remainder can also be defined for polynomials: given two polynomials p and q, where q ≠ 0, one can write
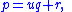
where the quotient u and the remainder r are polynomials, the degree of r is less than the degree of q, and a decomposition with these properties is unique. The quotient and the remainder are found using the polynomial long division
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
. The degree of the polynomial now plays a role similar to the absolute value of an integer: it is strictly less in the remainder r than it is in q, and when repeating this step such decrease cannot go on indefinitely. Therefore eventually some division will be exact, at which point the last non-zero remainder is the greatest common divisor of the initial two polynomials. Using the existence of greatest common divisors, Gauss was able to simultaneously rigorously prove the fundamental theorem of arithmetic for integers and its generalization to polynomials. In fact there exist other commutative rings than Z and K[X] that similarly admit an analogue of the Euclidean algorithm; all such rings are called Euclidean rings. Rings for which there exists unique (in an appropriate sense) factorization of nonzero elements into irreducible
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
factors are called unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s or factorial rings; the given construction shows that all Euclidean rings, and in particular Z and K[X], are unique factorization domains.
Another corollary of the polynomial division with the remainder is the fact that every proper ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
I of K[X] is principal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
, i.e. I consists of the multiples of a single polynomial f. Thus the polynomial ring K[X] is a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
, and for the same reason every Euclidean domain is a principal ideal domain. Also every principal ideal domain is a unique-factorization domain. These deductions make essential use of the fact that the polynomial coefficients lie in a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, namely in the polynomial division step, which requires the leading coefficient of q, which is only known to be non-zero, to have an inverse. If R is an integral domain that is not a field then R[X] is neither a Euclidean domain nor a principal ideal domain; however it could still be a unique factorization domain (and will be so if and only it R itself is a unique factorization domain, for instance if it is Z or another polynomial ring).
Quotient ring of K[X]
The ring K[X] of polynomials over K is obtained from K by adjoining one element, X. It turns out that any commutative ring L containing K and generated as a ring by a single element in addition to K can be described using K[X]. In particular, this applies to finite field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s of K.
Suppose that a commutative ring L contains K and there exists an element θ of L such that the ring L is generated by θ over K. Thus any element of L is a linear combination of powers of θ with coefficients in K. Then there is a unique ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
φ from K[X] into L which does not affect the elements of K itself (it is the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on K) and maps each power of X to the same power of θ. Its effect on the general polynomial amounts to "replacing X with θ":
-
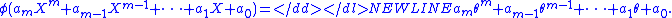
By the assumption, any element of L appears as the right hand side of the last expression for suitable m and elements a0, …, am of K. Therefore, φ is surjective and L is a homomorphic image of K[X]. More formally, let Ker φ be the kernelKernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of φ. It is an idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of K[X] and by the first isomorphism theoremIsomorphism theoremIn mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
for rings, L is isomorphic to the quotient of the polynomial ring K[X] by the ideal Ker φ. Since the polynomial ring is a principal ideal domain, this ideal is principalPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
: there exists a polynomial p∈K[X] such that
A particularly important application is to the case when the larger ring L is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Then the polynomial p must be irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
. Conversely, the primitive element theoremPrimitive element theoremIn mathematics, more specifically in the area of modern algebra known as field theory, the primitive element theorem or Artin's theorem on primitive elements is a result characterizing the finite degree field extensions that possess a primitive element...
states that any finite separable field extension L/K can be generated by a single element θ∈L and the preceding theory then gives a concrete description of the field L as the quotient of the polynomial ring K[X] by a principal ideal generated by an irreducible polynomial p. As an illustration, the field C of complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s is an extension of the field R of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s generated by a single element i such that i2 + 1 = 0. Accordingly, the polynomial X2 + 1 is irreducible over R and
More generally, given a (not necessarily commutative) ring A containing K and an element a of A that commutes with all elements of K, there is a unique ring homomorphism from the polynomial ring K[X] to A that maps X to a:
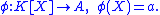
This homomorphism is given by the same formula as before, but it is not surjective in general. The existence and uniqueness of such a homomorphism φ expresses a certain universal propertyUniversal propertyIn various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
of the ring of polynomials in one variable and explains ubiquity of polynomial rings in various questions and constructions of ring theoryRing theoryIn abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
and commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
.
Polynomials
A polynomial in n variables X1,…, Xn with coefficients in a field K is defined analogously to a polynomial in one variable, but the notation is more cumbersome. For any multi-index α = (α1,…, αn), where each αi is a non-negative integer, let
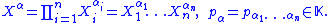
The product Xα is called the monomialMonomialIn mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
of multidegree α. A polynomial is a finite linear combination of monomials with coefficients in K
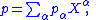
and only finitely many coefficients pα are different from 0. The degree of a monomial Xα, frequently denoted |α|, is defined as
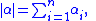
and the degree of a polynomial p is the largest degree of a monomial occurring with non-zero coefficient in the expansion of p.
The polynomial ring
Polynomials in n variables with coefficients in K form a commutative ring denoted
K[X1,…, Xn], or sometimes K[X], where X is a symbol representing the full set of variables, X = (X1,…, Xn), and called the polynomial ring in n variables. The polynomial ring in n variables can be obtained by repeated application of K[X] (the order by which is irrelevant). For example, K[X1, X2] is isomorphic to K[X1][X2]. This ring plays fundamental role in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. Many results in commutativeCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and homological algebraHomological algebraHomological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
originated in the study of its ideals and modules over this ring.
A polynomial ring with coefficients in
is the free commutative ring over its set of variables.
Hilbert's Nullstellensatz
A group of fundamental results concerning the relation between ideals of the polynomial ring K[X1,…, Xn] and algebraic subsetsAlgebraic setIn mathematics, an algebraic set over an algebraically closed field K is the set of solutions in Kn of a set of simultaneous equationsand so on up to...
of Kn originating with David HilbertDavid HilbertDavid Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
is known under the name Nullstellensatz (literally: "zero-locus theorem").
- (Weak form, algebraically closed field of coefficients). Let K be an algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
. Then every maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
m of K[X1,…, Xn] has the form
-
-
- (Weak form, any field of coefficients). Let k be a field, K be an algebraically closed field extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of k, and I be an ideal in the polynomial ring k[X1,…, Xn]. Then I contains 1 if and only if the polynomials in I do not have any common zero in Kn.
- (Strong form). Let k be a field, K be an algebraically closed field extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of k, I be an ideal in the polynomial ring k[X1,…, Xn],and V(I) be the algebraic subset of Kn defined by I. Suppose that f is a polynomial which vanishes at all points of V(I). Then some power of f belongs to the ideal I:
- Using the notion of the radical of an idealRadical of an idealIn commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
, the conclusion says that f belongs to the radical of I. As a corollary of this form of Nullstellensatz, there is a bijective correspondence between the radical ideals of K[X1,…, Xn] for an algebraically closed field K and the algebraic subsets of the n-dimensional affine spaceAffine spaceIn mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
Kn. It arises from the map
- The prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s of the polynomial ring correspond to irreducibleIrreducible componentIn mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
subvarieties of Kn.
Properties of the ring extension R ⊂ R[X]
One of the basic techniques in commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
is to relate properties of a ring with properties of its subringSubringIn mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
s. The notation R ⊂ S indicates that a ring R is a subring of a ring S. In this case S is called an overring of R and one speaks of a ring extension. This works particularly well for polynomial rings and allows one to establish many important properties of the ring of polynomials in several variables over a field, K[X1,…, Xn], by induction in n.
Summary of the results
In the following properties, R is a commutative ring and S = R[X1,…, Xn] is the ring of polynomials in n variables over R. The ring extension R ⊂ S can be built from R in n steps, by successively adjoining X1,…, Xn. Thus to establish each of the properties below, it is sufficient to consider the case n = 1.
- If R is an integral domain then the same holds for S.
- If R is a unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
then the same holds for S. The proof is based on the Gauss lemmaGauss's lemma (polynomial)In algebra, in the theory of polynomials , Gauss's lemma is either of two related statements about polynomials with integer coefficients:...
.
- Hilbert's basis theoremHilbert's basis theoremIn mathematics, specifically commutative algebra, Hilbert's basis theorem states that every ideal in the ring of multivariate polynomials over a Noetherian ring is finitely generated. This can be translated into algebraic geometry as follows: every algebraic set over a field can be described as the...
: If R is a Noetherian ringNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, then the same holds for S.
- Suppose that R is a Noetherian ring of finite global dimensionGlobal dimensionIn ring theory and homological algebra, the global dimension of a ring A denoted gl dim A, is a non-negative integer or infinity which is a homological invariant of the ring. It is defined to be the supremum of the set of projective dimensions of all A-modules...
. Then
- An analogous result holds for Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
.
Generalizations
Polynomial rings have been generalized in a great many ways, including polynomial rings with generalized exponents, power series rings, noncommutative polynomial rings, and skew-polynomial rings.
Infinitely many variables
The possibility to allow an infinite set of indeterminates is not really a generalization, as the ordinary notion of polynomial ring allows for it. It is then still true that each monomial involves only a finite number of indeterminates (so that its degree remains finite), and that each polynomial is a linear combination of monomials, which by definition involves only finitely many of them. This explains why such polynomial rings are relatively seldom considered: each individual polynomial involves only finitely many indeterminates, and even any finite computation involving polynomials remains inside some subring of polynomials in finitely many indeterminates.
In the case of infinitely many indeterminates, one can consider a ring strictly larger than the polynomial ring but smaller than the power series ring, by taking the subring of the latter formed by power series whose monomials have a bounded degree. Its elements still have a finite degree and are therefore are somewhat like polynomials, but it is possible for instance to take the sum of all indeterminates, which is not a polynomial. A ring of this kind plays a role in constructing the ring of symmetric functions.
Generalized exponents
A simple generalization only changes the set from which the exponents on the variable are drawn. The formulas for addition and multiplication make sense as long as one can add exponents: Xi·Xj = Xi+j. A set for which addition makes sense (is closed and associative) is called a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. The set of functions from a monoid N to a ring R which are nonzero at only finitely many places can be given the structure of a ring known as R[N], the monoid ring of N with coefficients in R. The addition is defined component-wise, so that if c = a+b, then cn = an + bn for every n in N. The multiplication is defined as the Cauchy product, so that if c = a·b, then for each n in N, cn is the sum of all aibj where i, j range over all pairs of elements of N which sum to n.
When N is commutative, it is convenient to denote the function a in R[N] as the formal sum: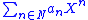
and then the formulas for addition and multiplication are the familiar: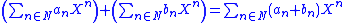
and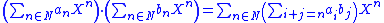
where the latter sum is taken over all i, j in N that sum to n.
Some authors such as go so far as to take this monoid definition as the starting point, and regular single variable polynomials are the special case where N is the monoid of non-negative integers. Polynomials in several variables simply take N to be the direct product of several copies of the monoid of non-negative integers.
Several interesting examples of rings and groups are formed by taking N to be the additive monoid of non-negative rational numbers, .
Power series
Power series generalize the choice of exponent in a different direction by allowing infinitely many nonzero terms. This requires various hypotheses on the monoid N used for the exponents, to ensure that the sums in the Cauchy product are finite sums. Alternatively, a topology can be placed on the ring, and then one restricts to convergent infinite sums. For the standard choice of N, the non-negative integers, there is no trouble, and the ring of formal power series is defined as the set of functions from N to a ring R with addition component-wise, and multiplication given by the Cauchy product. The ring of power series can be seen as the completion of the polynomial ring.
Noncommutative polynomial rings
For polynomial rings of more than one variable, the products X·Y and Y·X are simply defined to be equal. A more general notion of polynomial ring is obtained when the distinction between these two formal products is maintained. Formally, the polynomial ring in n noncommuting variables with coefficients in the ring R is the monoid ring R[N], where the monoid N is the free monoid on n letters, also known as the set of all strings over an alphabet of n symbols, with multiplication given by concatenation. Neither the coefficients nor the variables need commute amongst themselves, but the coefficients and variables commute with each other.
Just as the polynomial ring in n variables with coefficients in the commutative ring R is the free commutative R-algebra of rank n, the noncommutative polynomial ring in n variables with coefficients in the commutative ring R is the free associative, unital R-algebra on n generators, which is noncommutative when n > 1.
Differential and skew-polynomial rings
Other generalizations of polynomials are differential and skew-polynomial rings.
A differential polynomial ring is formed from a ring R and a derivation δ of R into R. Then the multiplication is extended from the relation X·a = a·X + δ(a). The standard example, called a Weyl algebra, takes R to be a polynomial ring k[t], and X to be the standard polynomial derivative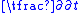
. One views the elements of R[X] as differential operators on the polynomial ring k[t], with elements f(t) of R=k[t] acting as multiplication, and X acting as the derivative in t. Labelling t = Y, one gets the canonical commutation relationCanonical commutation relationIn physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...
, X·Y − Y·X = 1, making the ring explicitly a Weyl algebra. This is a fundamentally important ring, .
The skew-polynomial ring is defined for a ring R and a ring endomorphism f of R, multiplication is extended from the relation X·r = f(r)·X to give an associative multiplication that distributes over the standard addition. More generally, one has a homomorphism F from the monoid N into the endomorphism ring of R, and Xn·r = F(n)(r)·Xn, as in . Skew polynomial rings are closely related to crossed productCrossed productIn mathematics, and more specifically in the theory of von Neumann algebras, a crossed productis a basic method of constructing a new von Neumann algebra froma von Neumann algebra acted on by a group. It is related to...
algebras. - (Weak form, any field of coefficients). Let k be a field, K be an algebraically closed field extension
-
-
