Radical of an ideal
Encyclopedia
In commutative ring
theory, a branch of mathematics
, the radical of an ideal I is an ideal
such that an element x is in the radical if some power of x is in I. A radical ideal (or semiprime ideal) is an ideal that is its own radical (this can be phrased as being a fixed point
of an operation on ideals called 'radicalization'). The radical of a primary ideal
is prime.
Radical ideals defined here are generalized to noncommutative rings in the Semiprime ring
article.
R, denoted by Rad(I) or √I, is defined as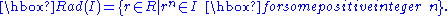
Intuitively, one can think of the radical of I as obtained by taking all the possible roots of elements of I. Rad(I) turns out to be an ideal itself, containing I.
The easiest way to prove that the radical of I of a ring A is an ideal is to note that it is the pre-image of the ideal of nilpotent elements in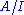
. In fact, one often takes this identification as a definition of radical.
If an ideal I coincides with its own radical, then I is called a radical ideal.
s.
The radical of a primary ideal
is prime.
elements of R, which will be called the nilradical of R (and will be denoted by N(R)). One can easily see that the nilradical of R is just the radical of the zero ideal (0). This permits an alternative definition for the (general) radical of an ideal I in R. Define Rad(I) as the preimage of N(R/I), the nilradical of R/I, under the projection map R→R/I.
To see that the two definitions for the radical of I are equivalent, note first that if r is in the preimage of √(R/I), then for some n, r n is zero in R/I, and hence r n is in I. Second, if r n is in I for some n, then the image of r n in R/I is zero, and hence r n is in the preimage of √(R/I).
This alternative definition can be very useful, as we shall see right below. See #Properties below for another characterization of the nilradical.
in commutative algebra
. An easily understood version of this theorem states that for an algebraically closed field
k, and for any finitely generated polynomial ideal J in the n indeterminates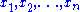
over the field k, one has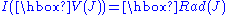
where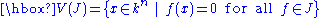
and
Another way of putting it: The composition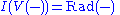
on the set of ideals of a ring is in fact a closure operator
. From the definition of the radical, it is clear that taking the radical is an idempotent operation.
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
theory, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the radical of an ideal I is an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
such that an element x is in the radical if some power of x is in I. A radical ideal (or semiprime ideal) is an ideal that is its own radical (this can be phrased as being a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of an operation on ideals called 'radicalization'). The radical of a primary ideal
Primary ideal
In mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
is prime.
Radical ideals defined here are generalized to noncommutative rings in the Semiprime ring
Semiprime ring
In ring theory, semiprime ideals and semiprime rings are generalizations of prime ideals and prime rings. The class of semiprime rings includes semiprimitive rings, prime rings and reduced rings....
article.
Definition
The radical of an ideal I in a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R, denoted by Rad(I) or √I, is defined as
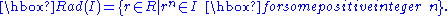
Intuitively, one can think of the radical of I as obtained by taking all the possible roots of elements of I. Rad(I) turns out to be an ideal itself, containing I.
The easiest way to prove that the radical of I of a ring A is an ideal is to note that it is the pre-image of the ideal of nilpotent elements in
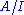. In fact, one often takes this identification as a definition of radical.If an ideal I coincides with its own radical, then I is called a radical ideal.
Examples
Consider the ring Z of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
- The radical of the ideal 4Z of integer multiples of 4 is 2Z.
- The radical of 5Z is 5Z.
- The radical of 12Z is 6Z.
- In general, the radical of mZ is rZ, where r is the product of all prime factors of m that are less than m. (see radical of an integer)
The radical of a primary ideal
Primary ideal
In mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
is prime.
The nilradical of a ring
Consider the set of all nilpotentNilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements of R, which will be called the nilradical of R (and will be denoted by N(R)). One can easily see that the nilradical of R is just the radical of the zero ideal (0). This permits an alternative definition for the (general) radical of an ideal I in R. Define Rad(I) as the preimage of N(R/I), the nilradical of R/I, under the projection map R→R/I.
To see that the two definitions for the radical of I are equivalent, note first that if r is in the preimage of √(R/I), then for some n, r n is zero in R/I, and hence r n is in I. Second, if r n is in I for some n, then the image of r n in R/I is zero, and hence r n is in the preimage of √(R/I).
This alternative definition can be very useful, as we shall see right below. See #Properties below for another characterization of the nilradical.
Properties
- If P is a prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
, then R/P is an integral domain, so it cannot have zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, and in particular it cannot have nonzero nilpotents. Hence, the nilradical of R/P is {0}, and its preimage, being P, is a radical ideal.
- By using localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
, we can see that Rad(I) is the intersection of all the prime ideals of R that contain I: Every prime ideal is radical, so the intersection J of the prime ideals containing I contains Rad(I). If r is an element of R which is not in Rad(I), then we let S be the set {rn|n is a nonnegative integer}. S is multiplicatively closed, so we can form the localization S-1R. Form the quotient S-1R/S-1I. By Zorn's lemmaZorn's lemmaZorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
we can choose a maximal ideal P in this ring. The preimage of P under the maps R→S-1R→S-1R/S-1I is a prime ideal which contains I and does not meet S; in particular, it does not meet r, so r is not in J.
- In particular, the nilradical is equal to the intersection of all prime ideals containing the 0 ideal, but all ideals must contain 0 so the nilradical can alternatively be defined as the intersection of the prime ideals.
Applications
The primary motivation in studying radicals is the celebrated Hilbert's NullstellensatzHilbert's Nullstellensatz
Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
. An easily understood version of this theorem states that for an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
k, and for any finitely generated polynomial ideal J in the n indeterminates
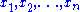over the field k, one has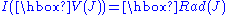where
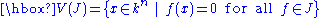
and
Another way of putting it: The composition
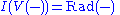on the set of ideals of a ring is in fact a closure operatorClosure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
. From the definition of the radical, it is clear that taking the radical is an idempotent operation.