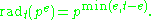Radical of an integer
Encyclopedia
In number theory
, the radical of a positive integer
n is defined as the product of the prime number
s dividing n:
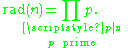
For example,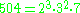
and therefore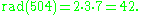
is multiplicative
(but not completely multiplicative
).
The radical of any integer n is the largest square-free
divisor of n, and so also described as the square-free kernel of n.
The definition is generalized to the largest t-free divisor of n,
, which are multiplicative functions
which act on prime powers as
The cases t=3 and t=4 are tabulated in and .
One of the most striking applications of the notion of radical occurs in the abc conjecture
, which states that, for any ε > 0, there exists a finite Kε such that, for all triples of coprime
positive integers a, b, and c satisfying a + b = c,
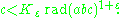
Furthermore, it can be shown that the nilpotent
elements of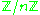
are all of the multiples of rad(n).
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the radical of a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n is defined as the product of the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s dividing n:
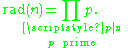
Examples
Radical numbers for the first few positive integers are- 1, 2, 3, 2, 5, 6, 7, 2, 3, 1010 (number)10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, ... .
For example,
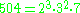
and therefore
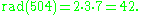
Properties
The function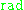 is multiplicativeMultiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
(but not completely multiplicative
Completely multiplicative function
In number theory, functions of positive integers which respect products are important and are called completely multiplicative functions or totally multiplicative functions. Especially in number theory, a weaker condition is also important, respecting only products of coprime numbers, and such...
).
The radical of any integer n is the largest square-free
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
divisor of n, and so also described as the square-free kernel of n.
The definition is generalized to the largest t-free divisor of n,
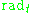, which are multiplicative functionswhich act on prime powers as
The cases t=3 and t=4 are tabulated in and .
One of the most striking applications of the notion of radical occurs in the abc conjecture
Abc conjecture
The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser in 1985. The conjecture is stated in terms of three positive integers, a, b and c , which have no common factor and satisfy a + b = c...
, which states that, for any ε > 0, there exists a finite Kε such that, for all triples of coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
positive integers a, b, and c satisfying a + b = c,
Furthermore, it can be shown that the nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements of
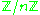are all of the multiples of rad(n).