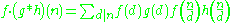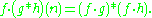Completely multiplicative function
Encyclopedia
In number theory
, functions of positive integers which respect products are important and are called completely multiplicative functions or totally multiplicative functions. Especially in number theory, a weaker condition is also important, respecting only products of coprime
numbers, and such functions are called multiplicative function
s. Outside of number theory, the term "multiplicative function" is often taken to be synonymous with "completely multiplicative function" as defined in this article.
(that is, a function whose domain
is the natural number
s), such that f(1) = 1 and f(ab) = f(a) f(b) holds for all positive integers a and b.
Without the requirement that f(1) = 1, one could still have f(1) = 0, but then f(a) = 0 for all positive integers a, so this is not a very strong restriction.
with leading coefficient 1: For any particular positive integer n, define f(a) = an.
The Liouville function is a non-trivial example of a completely multiplicative function as are Dirichlet character
s.
. Thus, if n is a product of powers of distinct primes, say n = pa qb ..., then f(n) = f(p)a f(q)b ...
While the Dirichlet convolution
of two multiplicative functions is multiplicative, the Dirichlet convolution
of two completely multiplicative functions need not be completely multiplicative.
There are a variety of statements about a function which are equivalent to it being completely multiplicative. For example, if a function f multiplicative then is completely multiplicative if and only if the Dirichlet inverse is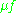 where
where 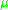 is the Mobius function
is the Mobius function
.
Completely multiplicative functions also satisfy a pseudo-associative law. If f is completely multiplicative then
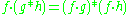
where * represents the Dirichlet product and represents pointwise multiplication.. One consequence of this is that for any completely multiplicative function f one has
represents pointwise multiplication.. One consequence of this is that for any completely multiplicative function f one has
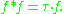
Here is the divisor function
is the divisor function
.
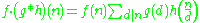
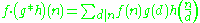
 (since f is completely multiplicative)
(since f is completely multiplicative)
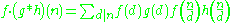
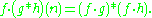
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, functions of positive integers which respect products are important and are called completely multiplicative functions or totally multiplicative functions. Especially in number theory, a weaker condition is also important, respecting only products of coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
numbers, and such functions are called multiplicative function
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
s. Outside of number theory, the term "multiplicative function" is often taken to be synonymous with "completely multiplicative function" as defined in this article.
Definition
A completely multiplicative function (or totally multiplicative function) is an arithmetic functionArithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
(that is, a function whose domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
is the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s), such that f(1) = 1 and f(ab) = f(a) f(b) holds for all positive integers a and b.
Without the requirement that f(1) = 1, one could still have f(1) = 0, but then f(a) = 0 for all positive integers a, so this is not a very strong restriction.
Examples
The easiest example of a multiplicative function is a monomialMonomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
with leading coefficient 1: For any particular positive integer n, define f(a) = an.
The Liouville function is a non-trivial example of a completely multiplicative function as are Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
s.
Properties
A completely multiplicative function is completely determined by its values at the prime numbers, a consequence of the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. Thus, if n is a product of powers of distinct primes, say n = pa qb ..., then f(n) = f(p)a f(q)b ...
While the Dirichlet convolution
Dirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
of two multiplicative functions is multiplicative, the Dirichlet convolution
Dirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
of two completely multiplicative functions need not be completely multiplicative.
There are a variety of statements about a function which are equivalent to it being completely multiplicative. For example, if a function f multiplicative then is completely multiplicative if and only if the Dirichlet inverse is
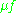 where
where 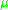 is the Mobius function
is the Mobius functionMöbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
Completely multiplicative functions also satisfy a pseudo-associative law. If f is completely multiplicative then
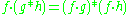
where * represents the Dirichlet product and
 represents pointwise multiplication.. One consequence of this is that for any completely multiplicative function f one has
represents pointwise multiplication.. One consequence of this is that for any completely multiplicative function f one has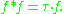
Here
 is the divisor function
is the divisor functionDivisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
.
Proof of pseudo-associative property
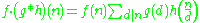
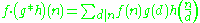
 (since f is completely multiplicative)
(since f is completely multiplicative)