Dirichlet character
Encyclopedia
In number theory
, Dirichlet characters are certain arithmetic function
s which arise from completely multiplicative characters
on the units of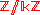
. Dirichlet characters are used to define Dirichlet L-functions, which are meromorphic function
s with a variety of interesting analytic properties.
If
is a Dirichlet character, one defines its Dirichlet L-series by
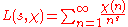
where s is a complex number
with real part > 1. By analytic continuation
, this function can be extended to a meromorphic function
on the whole complex plane
. Dirichlet L-functions are generalizations of the Riemann zeta-function and appear prominently in the generalized Riemann hypothesis
.
Dirichlet characters are named in honour of Johann Peter Gustav Lejeune Dirichlet
.
χ from the integer
s to the complex number
s which has the following properties:
From this definition, several other properties can be deduced.
By property 3), χ(1)=χ(1×1)=χ(1)χ(1). Since gcd(1, k) = 1, property 2) says χ(1) ≠ 0, so
Properties 3) and 4) show that every Dirichlet character χ is completely multiplicative.
Property 1) says that a character is periodic
with period k; we say that χ is a character to the modulus k. This is equivalent to saying that
If gcd(a,k) = 1, Euler's theorem says that aφ(k) ≡ 1 (mod k) (where φ(k) is the totient function). Therefore by 5) and 4), χ(aφ(k)) = χ(1) = 1, and by 3), χ(aφ(k)) =χ(a)φ(k). So
The unique character of period 1 is called the trivial character. Note that any character vanishes at 0 except the trivial one, which is 1 on all integers.
A character is called principal if it assumes the value 1 for arguments coprime to its modulus and otherwise is 0. A character is called real if it assumes real values only. A character which is not real is called complex.
The sign of the character χ depends on its value at −1. Specifically, χ is said to be odd if χ(−1) = −1 and even if χ(−1) = 1.
of the
unit group of the ring Z/kZ, as given below.
k:
That is, the residue class
is the coset
of n in the quotient ring
Z/kZ.
The set of units modulo k forms an abelian group
of order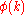
, where group multiplication is given by
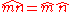and 
again denotes Euler's phi function.
The identity in this group is the residue class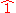
and the inverse of 
is the residue class 
where
, i.e., 
. For example, for k=6, the set of units is 
because 0, 2, 3, and 4 are not coprime to 6.
from the unit group modulo k to the non-zero complex numbers
,
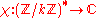necessarily with values that are roots of unity since the units modulo k form a finite group. We can lift
to a completely multiplicative function on integers relatively prime to k and then to all integers by extending the function to be 0 on integers having a non-trivial factor in common with k. The principal character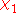 
modulo k has the properties
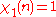if gcd(n, k) = 1 and
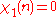if gcd(n, k) > 1.
When k is 1, the principal character modulo k is equal to 1 at all integers. For k greater than 1, the principal character modulo k vanishes at integers having a non-trivial common factor with k and is 1 at other integers.
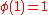character modulo 1:
This is the trivial character.
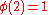character modulo 2:
Note that χ is wholly determined by χ(1) since 1 generates the group of units modulo 2.
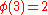characters modulo 3:
Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 3.
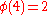characters modulo 4:
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 4.
The Dirichlet L-series for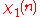
is
the Dirichlet lambda function (closely related to the Dirichlet eta function)
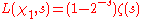
where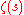
is the Riemann zeta-function. The L-series for 
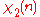is the Dirichlet beta-function
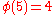characters modulo 5. In the tables, i is a square root of 
.
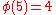Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 5.
characters modulo 6:
Note that χ is wholly determined by χ(5) since 5 generates the group of units modulo 6.
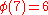characters modulo 7. In the table below,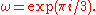 
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 7.
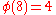characters modulo 8.
Note that χ is wholly determined by χ(3) and χ(5) since 3 and 5 generate the group of units modulo 8.
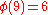characters modulo 9. In the table below,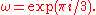 
Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 9.
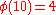characters modulo 10.
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 10.
, then the function
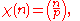where 
is the Legendre symbol
, is a Dirichlet character modulo p.
More generally, if m is an odd number the function
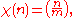where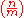 
is the Jacobi symbol
, is a Dirichlet character modulo m. These are called the quadratic characters.
s.
, in 1831, in order to prove Dirichlet's theorem on arithmetic progressions
. He only studied them for real s and especially as s tends to 1. The extension of these functions to complex s in the whole complex plane was obtained by Bernhard Riemann
in 1859.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Dirichlet characters are certain arithmetic function
Arithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
s which arise from completely multiplicative characters
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
on the units of
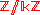. Dirichlet characters are used to define Dirichlet L-functions, which are meromorphic functionMeromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s with a variety of interesting analytic properties.
If
is a Dirichlet character, one defines its Dirichlet L-series by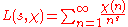where s is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
with real part > 1. By analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
, this function can be extended to a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
on the whole complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. Dirichlet L-functions are generalizations of the Riemann zeta-function and appear prominently in the generalized Riemann hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
.
Dirichlet characters are named in honour of Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
.
Axiomatic definition
A Dirichlet character is any functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
χ from the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s to the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s which has the following properties:
- There exists a positive integer k such that χ(n) = χ(n + k) for all n.
- If gcdGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(n,k) > 1 then χ(n) = 0; if gcd(n,k) = 1 then χ(n) ≠ 0. - χ(mn) = χ(m)χ(n) for all integers m and n.
From this definition, several other properties can be deduced.
By property 3), χ(1)=χ(1×1)=χ(1)χ(1). Since gcd(1, k) = 1, property 2) says χ(1) ≠ 0, so
- χ(1) = 1.
Properties 3) and 4) show that every Dirichlet character χ is completely multiplicative.
Property 1) says that a character is periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
with period k; we say that χ is a character to the modulus k. This is equivalent to saying that
- If a ≡ b (mod k) then χ(a) = χ(b).
If gcd(a,k) = 1, Euler's theorem says that aφ(k) ≡ 1 (mod k) (where φ(k) is the totient function). Therefore by 5) and 4), χ(aφ(k)) = χ(1) = 1, and by 3), χ(aφ(k)) =χ(a)φ(k). So
- For all a relatively prime to k, χ(a) is a φ(k)-th complex root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
.
The unique character of period 1 is called the trivial character. Note that any character vanishes at 0 except the trivial one, which is 1 on all integers.
A character is called principal if it assumes the value 1 for arguments coprime to its modulus and otherwise is 0. A character is called real if it assumes real values only. A character which is not real is called complex.
The sign of the character χ depends on its value at −1. Specifically, χ is said to be odd if χ(−1) = −1 and even if χ(−1) = 1.
Construction via residue classes
Dirichlet characters may be viewed in terms of the character groupCharacter group
In mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory...
of the
unit group of the ring Z/kZ, as given below.
Residue classes
Given an integer k, one defines the residue class of an integer n as the set of all integers congruent to n moduloModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
k:
That is, the residue class
is the cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of n in the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
Z/kZ.
The set of units modulo k forms an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
of order
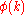, where group multiplication is given by 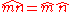and again denotes Euler's phi function.
The identity in this group is the residue class
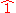and the inverse of is the residue class where, i.e., . For example, for k=6, the set of units is because 0, 2, 3, and 4 are not coprime to 6.Dirichlet characters
A Dirichlet character modulo k is a group homomorphism from the unit group modulo k to the non-zero complex numbers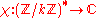,necessarily with values that are roots of unity since the units modulo k form a finite group. We can lift
Lift (mathematics)
In the branch of mathematics called category theory, given a morphism f from an object X to an object Y, and a morphism g from an object Z to Y, a lift of f to Z is a morphism h from X to Z such that gh = f.A basic example in topology is lifting a path in one space to a path in a covering space...
to a completely multiplicative function on integers relatively prime to k and then to all integers by extending the function to be 0 on integers having a non-trivial factor in common with k. The principal character 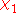modulo k has the properties 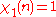if gcd(n, k) = 1 and 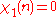if gcd(n, k) > 1.When k is 1, the principal character modulo k is equal to 1 at all integers. For k greater than 1, the principal character modulo k vanishes at integers having a non-trivial common factor with k and is 1 at other integers.
A few character tables
The tables below help illustrate the nature of a Dirichlet character. They present all of the characters from modulus 1 to modulus 10. The characters χ1 are the principal characters.Modulus 1
There is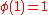 character modulo 1:| χ \ n | 0 |
 |
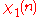1 |
This is the trivial character.
Modulus 2
There is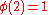 character modulo 2:| χ \ n | 0 | 1 |
 |
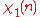0 | 1 |
Note that χ is wholly determined by χ(1) since 1 generates the group of units modulo 2.
Modulus 3
There are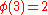 characters modulo 3:| χ \ n | 0 | 1 | 2 |
 |
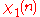0 | 1 | 1 |
 |
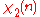0 | 1 | −1 |
Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 3.
Modulus 4
There are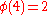 characters modulo 4:| χ \ n | 0 | 1 | 2 | 3 |
 |
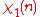0 | 1 | 0 | 1 |
 |
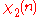0 | 1 | 0 | −1 |
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 4.
The Dirichlet L-series for
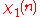isthe Dirichlet lambda function (closely related to the Dirichlet eta function)
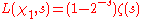
where
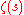is the Riemann zeta-function. The L-series for 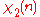is the Dirichlet beta-functionDirichlet beta function
In mathematics, the Dirichlet beta function is a special function, closely related to the Riemann zeta function...
Modulus 5
There are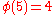 characters modulo 5. In the tables, i is a square root of 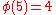.| χ \ n | 0 | 1 | 2 | 3 | 4 |
 |
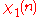0 | 1 | 1 | 1 | 1 |
 |
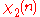0 | 1 | i | −i | −1 |
 |
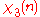0 | 1 | −1 | −1 | 1 |
 |
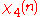0 | 1 | −i | i | −1 |
Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 5.
Modulus 6
There are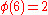 characters modulo 6:| χ \ n | 0 | 1 | 2 | 3 | 4 | 5 |
 |
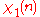0 | 1 | 0 | 0 | 0 | 1 |
 |
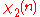0 | 1 | 0 | 0 | 0 | −1 |
Note that χ is wholly determined by χ(5) since 5 generates the group of units modulo 6.
Modulus 7
There are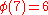 characters modulo 7. In the table below,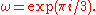 | χ \ n | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
 |
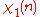0 | 1 | 1 | 1 | 1 | 1 | 1 |
 |
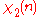0 | 1 | ω2 | ω | −ω | −ω2 | −1 |
 |
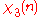0 | 1 | −ω | ω2 | ω2 | −ω | 1 |
 |
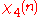0 | 1 | 1 | −1 | 1 | −1 | −1 |
 |
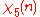0 | 1 | ω2 | −ω | −ω | ω2 | 1 |
 |
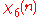0 | 1 | −ω | −ω2 | ω2 | ω | −1 |
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 7.
Modulus 8
There are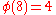 characters modulo 8.| χ \ n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
 |
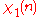0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
 |
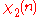0 | 1 | 0 | 1 | 0 | −1 | 0 | −1 |
 |
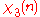0 | 1 | 0 | −1 | 0 | 1 | 0 | −1 |
 |
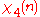0 | 1 | 0 | −1 | 0 | −1 | 0 | 1 |
Note that χ is wholly determined by χ(3) and χ(5) since 3 and 5 generate the group of units modulo 8.
Modulus 9
There are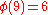 characters modulo 9. In the table below,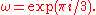 | χ \ n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
 |
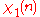0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
 |
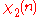0 | 1 | ω | 0 | ω2 | −ω2 | 0 | −ω | −1 |
 |
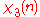0 | 1 | ω2 | 0 | −ω | −ω | 0 | ω2 | 1 |
 |
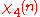0 | 1 | −1 | 0 | 1 | −1 | 0 | 1 | −1 |
 |
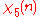0 | 1 | −ω | 0 | ω2 | ω2 | 0 | −ω | 1 |
 |
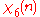0 | 1 | −ω2 | 0 | −ω | ω | 0 | ω2 | −1 |
Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 9.
Modulus 10
There are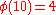 characters modulo 10.| χ \ n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
 |
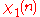0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
 |
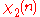0 | 1 | 0 | i | 0 | 0 | 0 | −i | 0 | −1 |
 |
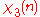0 | 1 | 0 | −1 | 0 | 0 | 0 | −1 | 0 | 1 |
 |
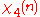0 | 1 | 0 | −i | 0 | 0 | 0 | i | 0 | −1 |
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 10.
Examples
If p is a prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, then the function
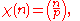where is the Legendre symbolLegendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
, is a Dirichlet character modulo p.
More generally, if m is an odd number the function
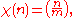where 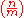is the Jacobi symbolJacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
, is a Dirichlet character modulo m. These are called the quadratic characters.
Conductors
Residues mod N give rise to residues mod M, for any factor M of N, by discarding some information. The effect on Dirichlet characters goes in the opposite direction: if χ is a character mod M, it gives rise to a character χ* mod N for any multiple N of M. With some attention to the values at which characters take the value 0, one gets the concept of a primitive Dirichlet character, one that does not arise from a factor; and the associated idea of conductor, i.e. the natural (smallest) modulus for a character. Imprimitive characters can cause missing Euler factors in L-functionL-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
s.
History
Dirichlet characters and their L-series were introduced by Johann Peter Gustav Lejeune DirichletJohann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
, in 1831, in order to prove Dirichlet's theorem on arithmetic progressions
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
. He only studied them for real s and especially as s tends to 1. The extension of these functions to complex s in the whole complex plane was obtained by Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
in 1859.
See also
- Character sumCharacter sumIn mathematics, a character sum is a sum\Sigma \chi\,of values of a Dirichlet character χ modulo N, taken over a given range of values of n. Such sums are basic in a number of questions, for example in the distribution of quadratic residues, and in particular in the classical question of finding an...
- Dirichlet L-function
- Gaussian sum
- Primitive root modulo nPrimitive root modulo nIn modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
- Selberg classSelberg classIn mathematics, the Selberg class S is an axiomatic definition of a class of L-functions. The members of the class are Dirichlet series which obey four axioms that seem to capture the essential properties satisfied by most functions that are commonly called L-functions or zeta functions...