
Abelian group
Encyclopedia
In abstract algebra
, an abelian group, also called a commutative group, is a group
in which the result of applying the group operation
to two group elements does not depend on their order (the axiom of commutativity
). Abelian groups generalize
the arithmetic
of addition of integer
s. They are named after Niels Henrik Abel
.
The concept of an abelian group is one of the first concepts encountered in undergraduate abstract algebra, with many other basic objects, such as a module
and a vector space
, being its refinements. The theory of abelian groups is generally simpler than that of their non-abelian
counterparts, and finite abelian groups are very well understood. On the other hand, the theory of infinite abelian groups is an area of current research.
"•" that combines any two elements a and b to form another element denoted . The symbol "•" is a general placeholder for a concretely given operation. To qualify as an abelian group, the set and operation, , must satisfy five requirements known as the abelian group axioms:
Closure: For all a, b in A, the result of the operation a • b is also in A.
Associativity: For all a, b and c in A, the equation (a • b) • c = a • (b • c) holds.
Identity element: There exists an element e in A, such that for all elements a in A, the equation e • a = a • e = a holds.
Inverse element: For each a in A, there exists an element b in A such that a • b = b • a = e, where e is the identity element.
Commutativity: For all a, b in A, a • b = b • a.
More compactly, an abelian group is a commutative group
. A group in which the group operation is not commutative is called a "non-abelian group" or "non-commutative group".
Generally, the multiplicative notation is the usual notation for groups, while the additive notation is the usual notation for modules
. The additive notation may also be used to emphasize that a particular group is abelian, whenever both abelian and non-abelian groups are considered.
is abelian, a table (matrix) - known as a Cayley table
- can be constructed in a similar fashion to a multiplication table
. If the group is G = {g1 = e, g2, ..., gn} under the operation ⋅, the (i, j)'th entry of this table contains the product gi ⋅ gj. The group is abelian if and only if
this table is symmetric about the main diagonal.
This is true since if the group is abelian, then gi ⋅ gj = gj ⋅ gi. This implies that the (i, j)'th entry of the table equals the (j, i)'th entry, thus the table is symmetric about the main diagonal.
In general, matrices
, even invertible matrices, do not form an abelian group under multiplication because matrix multiplication is generally not commutative. However, some groups of matrices are abelian groups under matrix multiplication - one example is the group of 2x2 rotation matrices.
mathematician
Niels Henrik Abel
by Camille Jordan
because Abel found that the commutativity of the group of an equation implies its roots are solvable by radicals. See Section 6.5 of Cox (2004) for more information on the historical background.
and x is an element of an abelian group G written additively, then nx can be defined as x + x + ... + x (n summands) and (−n)x = −(nx). In this way, G becomes a module
over the ring
Z of integers. In fact, the modules over Z can be identified with the abelian groups.
Theorems about abelian groups (i.e. module
s over the principal ideal domain
Z) can often be generalized to theorems about modules over an arbitrary principal ideal domain. A typical example is the classification of finitely generated abelian group
s which is a specialization of the structure theorem for finitely generated modules over a principal ideal domain
. In the case of finitely generated abelian groups, this theorem guarantees that an abelian group splits as a direct sum of a torsion group and a free abelian group. The former may be written as a direct sum of finitely many groups of the form Z/pkZ for p prime, and the latter is a direct sum of finitely many copies of Z.
If f, g : G → H are two group homomorphism
s between abelian groups, then their sum f + g, defined by (f + g)(x) = f(x) + g(x), is again a homomorphism. (This is not true if H is a non-abelian group.) The set Hom(G, H) of all group homomorphisms from G to H thus turns into an abelian group in its own right.
Somewhat akin to the dimension
of vector space
s, every abelian group has a rank
. It is defined as the cardinality
of the largest set of linearly independent elements of the group. The integers and the rational number
s have rank one, as well as every subgroup of the rationals.
, Z/nZ, were among the first examples of groups. It turns out that an arbitrary finite abelian group is isomorphic to a direct sum of finite cyclic groups of prime power order, and these orders are uniquely determined, forming a complete system of invariants. The automorphism group of a finite abelian group can be described directly in terms of these invariants. The theory had been first developed in the 1879 paper of Georg Frobenius and Ludwig Stickelberger
and later was both simplified and generalized to finitely generated modules over a principal ideal domain, forming an important chapter of linear algebra
.
-power order. This is a special case of the fundamental theorem of finitely generated abelian groups when G has zero rank
.
The cyclic group of order mn is isomorphic to the direct sum of
of order mn is isomorphic to the direct sum of 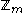 and
and 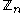 if and only if m and n are coprime
if and only if m and n are coprime
. It follows that any finite abelian group G is isomorphic to a direct sum of the form

in either of the following canonical ways:
For example,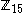 can be expressed as the direct sum of two cyclic subgroups of order 3 and 5:
can be expressed as the direct sum of two cyclic subgroups of order 3 and 5: 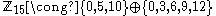 . The same can be said for any abelian group of order 15, leading to the remarkable conclusion that all abelian groups of order 15 are isomorphic
. The same can be said for any abelian group of order 15, leading to the remarkable conclusion that all abelian groups of order 15 are isomorphic
.
For another example, every abelian group of order 8 is isomorphic to either (the integers 0 to 7 under addition modulo 8),
(the integers 0 to 7 under addition modulo 8), 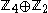 (the odd integers 1 to 15 under multiplication modulo 16), or
(the odd integers 1 to 15 under multiplication modulo 16), or 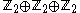 .
.
See also list of small groups for finite abelian groups of order 16 or less.
 K of subgroups of coprime
K of subgroups of coprime
order, then Aut(H K)
K) 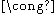 Aut(H)
Aut(H)  Aut(K).
Aut(K).
Given this, the fundamental theorem shows that to compute the automorphism group of G it suffices to compute the automorphism groups of the Sylow p-subgroups separately (that is, all direct sums of cyclic subgroups, each with order a power of p). Fix a prime p and suppose the exponents ei of the cyclic factors of the Sylow p-subgroup are arranged in increasing order:

for some n > 0. One needs to find the automorphisms of
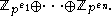
One special case is when n = 1, so that there is only one cyclic prime-power factor in the Sylow p-subgroup P. In this case the theory of automorphisms of a finite cyclic group
can be used. Another special case is when n is arbitrary but ei = 1 for 1 ≤ i ≤ n. Here, one is considering P to be of the form
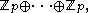
so elements of this subgroup can be viewed as comprising a vector space of dimension n over the finite field of p elements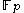 . The automorphisms of this subgroup are therefore given by the invertible linear transformations, so
. The automorphisms of this subgroup are therefore given by the invertible linear transformations, so
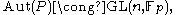
where GL is the appropriate general linear group
. This is easily shown to have order

In the most general case, where the ei and n are arbitrary, the automorphism group is more difficult to determine. It is known, however, that if one defines
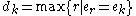
and
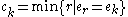
then one has in particular dk ≥ k, ck ≤ k, and

One can check that this yields the orders in the previous examples as special cases (see [Hillar,Rhea]).
A is isomorphic to the direct sum of r copies of Z and a finite abelian group, which in turn is decomposable into a direct sum of finitely many cyclic group
s of primary orders. Even though the decomposition is not unique, the number r, called the rank
of A, and the prime powers giving the orders of finite cyclic summands are uniquely determined.
By contrast, classification of general infinitely generated abelian groups is far from complete. Divisible group
s, i.e. abelian groups A in which the equation nx = a admits a solution x ∈ A for any natural number n and element a of A, constitute one important class of infinite abelian groups that can be completely characterized. Every divisible group is isomorphic to a direct sum, with summands isomorphic to Q and Prüfer group
s Qp/Zp for various prime numbers p, and the cardinality of the set of summands of each type is uniquely determined. Moreover, if a divisible group A is a subgroup of an abelian group G then A admits a direct complement: a subgroup C of G such that G = A ⊕ C. Thus divisible groups are injective module
s in the category of abelian groups, and conversely, every injective abelian group is divisible (Baer's criterion). An abelian group without non-zero divisible subgroups is called reduced.
Two important special classes of infinite abelian groups with diametrically opposite properties are torsion groups and torsion-free groups, examplified by the groups Q/Z (periodic) and Q (torsion-free).
or torsion if every element has finite order
. A direct sum of finite cyclic groups is periodic. Although the converse statement is not true in general, some special cases are known. The first and second Prüfer theorems
state that if A is a periodic group and either it has bounded exponent, i.e. nA = 0 for some natural number n, or if A is countable and the p-heights
of the elements of A are finite for each p, then A is isomorphic to a direct sum of finite cyclic groups. The cardinality of the set of direct summands isomorphic to Z/pmZ in such a decomposition is an invariant of A. These theorems were later subsumed in the Kulikov criterion. In a different direction, Helmut Ulm
found an extension of the second Prüfer theorem to countable abelian p-groups with elements of infinite height: those groups are completely classified by means of their Ulm invariants.
An abelian group that is neither periodic nor torsion-free is called mixed. If A is an abelian group and T(A) is its torsion subgroup then the factor group A/T(A) is torsion-free. However, in general the torsion subgroup is not a direct summand of A, so the torsion-free factor cannot be realized as a subgroup of A and A is not isomorphic to T(A) ⊕ A/T(A). Thus the theory of mixed groups involves more than simply combining the results about periodic and torsion-free groups.
: the cardinality of the maximal linearly independent subset of A. Abelian groups of rank 0 are precisely the periodic groups, while torsion-free abelian groups of rank 1
are necessarily subgroups of Q and can be completely described. More generally, a torsion-free abelian group of finite rank r is a subgroup of Qr. On the other hand, the group of p-adic integers Zp is a torsion-free abelian group of infinite Z-rank and the groups Zpn with different n are non-isomorphic, so this invariant does not even fully capture properties of some familiar groups.
The classification theorems for finitely generated, divisible, countable periodic, and rank 1 torsion-free abelian groups explained above were all obtained before 1950 and form a foundation of the classification of more general infinite abelian groups. Important technical tools used in classification of infinite abelian groups are pure
and basic
subgroups. Introduction of various invariants of torsion-free abelian groups has been one avenue of further progress. See the books by Irving Kaplansky
, László Fuchs, Phillip Griffiths
, and David Arnold, as well as the proceedings of the conferences on Abelian Group Theory published in Lecture Notes in Mathematics for more recent results.
is an abelian group, but not all abelian groups are additive groups of rings (with nontrivial multiplication). Some important topics in this area of study are:
, which turns them into topological group
s.
The collection of all abelian groups, together with the homomorphisms
between them, forms the category
Ab, the prototype of an abelian category
.
Nearly all well-known algebraic structure
s other than Boolean algebras, are undecidable
. Hence it is surprising that Tarski's student Szmielew (1955) proved that the first order theory of abelian groups, unlike its nonabelian counterpart, is decidable. This decidability, plus the fundamental theorem of finite abelian groups described above, highlight some of the successes in abelian group theory, but there are still many areas of current research:
Moreover, abelian groups of infinite order lead, quite surprisingly, to deep questions about the set theory
commonly assumed to underlie all of mathematics. Take the Whitehead problem
: are all Whitehead groups of infinite order also free abelian group
s? In the 1970s, Saharon Shelah
proved that the Whitehead problem is:
s derived from the proper name
of a mathematician
, the word "abelian" is rare in that it is often spelled with a lowercase a, rather than an uppercase A, indicating how ubiquitous the concept is in modern mathematics.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an abelian group, also called a commutative group, is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
in which the result of applying the group operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
to two group elements does not depend on their order (the axiom of commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
). Abelian groups generalize
Generalization
A generalization of a concept is an extension of the concept to less-specific criteria. It is a foundational element of logic and human reasoning. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements. As such, it...
the arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
of addition of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. They are named after Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
.
The concept of an abelian group is one of the first concepts encountered in undergraduate abstract algebra, with many other basic objects, such as a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, being its refinements. The theory of abelian groups is generally simpler than that of their non-abelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
counterparts, and finite abelian groups are very well understood. On the other hand, the theory of infinite abelian groups is an area of current research.
Definition
An abelian group is a set, A, together with an operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
"•" that combines any two elements a and b to form another element denoted . The symbol "•" is a general placeholder for a concretely given operation. To qualify as an abelian group, the set and operation, , must satisfy five requirements known as the abelian group axioms:
Closure: For all a, b in A, the result of the operation a • b is also in A.
Associativity: For all a, b and c in A, the equation (a • b) • c = a • (b • c) holds.
Identity element: There exists an element e in A, such that for all elements a in A, the equation e • a = a • e = a holds.
Inverse element: For each a in A, there exists an element b in A such that a • b = b • a = e, where e is the identity element.
Commutativity: For all a, b in A, a • b = b • a.
More compactly, an abelian group is a commutative group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. A group in which the group operation is not commutative is called a "non-abelian group" or "non-commutative group".
Notation
There are two main notational conventions for abelian groups — additive and multiplicative.| Convention | Operation | Identity | Powers | Inverse |
|---|---|---|---|---|
| Addition | x + y | 0 | nx | −x |
| Multiplication | x * y or xy | e or 1 | xn | x−1 |
Generally, the multiplicative notation is the usual notation for groups, while the additive notation is the usual notation for modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. The additive notation may also be used to emphasize that a particular group is abelian, whenever both abelian and non-abelian groups are considered.
Multiplication table
To verify that a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
is abelian, a table (matrix) - known as a Cayley table
Cayley table
A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
- can be constructed in a similar fashion to a multiplication table
Multiplication table
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
. If the group is G = {g1 = e, g2, ..., gn} under the operation ⋅, the (i, j)'th entry of this table contains the product gi ⋅ gj. The group is abelian if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
this table is symmetric about the main diagonal.
This is true since if the group is abelian, then gi ⋅ gj = gj ⋅ gi. This implies that the (i, j)'th entry of the table equals the (j, i)'th entry, thus the table is symmetric about the main diagonal.
Examples
- For the integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and the operation additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
"+", denoted (Z,+), the operation + combines any two integers to form a third integer, addition is associative, zero is the additive identityAdditive identityIn mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
, every integer n has an additive inverseAdditive inverseIn mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
, −n, and the addition operation is commutative since m + n = n + m for any two integers m and n.
- Every cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
G is abelian, because if x, y are in G, then xy = aman = am + n = an + m = anam = yx. Thus the integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, Z, form an abelian group under addition, as do the integers modulo nModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, Z/nZ.
- Every ringRing theoryIn abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
is an abelian group with respect to its addition operation. In a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
the invertible elements, or unitsUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
, form an abelian multiplicative groupMultiplicative groupIn mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
. In particular, the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s are an abelian group under addition, and the nonzero real numbers are an abelian group under multiplication.
- Every subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of an abelian group is normalNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, so each subgroup gives rise to a quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
. Subgroups, quotients, and direct sums of abelian groups are again abelian.
In general, matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, even invertible matrices, do not form an abelian group under multiplication because matrix multiplication is generally not commutative. However, some groups of matrices are abelian groups under matrix multiplication - one example is the group of 2x2 rotation matrices.
Historical remarks
Abelian groups were named for NorwegianNorway
Norway , officially the Kingdom of Norway, is a Nordic unitary constitutional monarchy whose territory comprises the western portion of the Scandinavian Peninsula, Jan Mayen, and the Arctic archipelago of Svalbard and Bouvet Island. Norway has a total area of and a population of about 4.9 million...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
by Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
because Abel found that the commutativity of the group of an equation implies its roots are solvable by radicals. See Section 6.5 of Cox (2004) for more information on the historical background.
Properties
If n is a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
and x is an element of an abelian group G written additively, then nx can be defined as x + x + ... + x (n summands) and (−n)x = −(nx). In this way, G becomes a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
Z of integers. In fact, the modules over Z can be identified with the abelian groups.
Theorems about abelian groups (i.e. module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over the principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
Z) can often be generalized to theorems about modules over an arbitrary principal ideal domain. A typical example is the classification of finitely generated abelian group
Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
s which is a specialization of the structure theorem for finitely generated modules over a principal ideal domain
Structure theorem for finitely generated modules over a principal ideal domain
In mathematics, in the field of abstract algebra, the structure theorem for finitely generated modules over a principal ideal domain is a generalization of the fundamental theorem of finitely generated abelian groups and roughly states that finitely generated modules can be uniquely decomposed in...
. In the case of finitely generated abelian groups, this theorem guarantees that an abelian group splits as a direct sum of a torsion group and a free abelian group. The former may be written as a direct sum of finitely many groups of the form Z/pkZ for p prime, and the latter is a direct sum of finitely many copies of Z.
If f, g : G → H are two group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s between abelian groups, then their sum f + g, defined by (f + g)(x) = f(x) + g(x), is again a homomorphism. (This is not true if H is a non-abelian group.) The set Hom(G, H) of all group homomorphisms from G to H thus turns into an abelian group in its own right.
Somewhat akin to the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, every abelian group has a rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
. It is defined as the cardinality
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
of the largest set of linearly independent elements of the group. The integers and the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s have rank one, as well as every subgroup of the rationals.
Finite abelian groups
Cyclic groups of integers modulo nModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, Z/nZ, were among the first examples of groups. It turns out that an arbitrary finite abelian group is isomorphic to a direct sum of finite cyclic groups of prime power order, and these orders are uniquely determined, forming a complete system of invariants. The automorphism group of a finite abelian group can be described directly in terms of these invariants. The theory had been first developed in the 1879 paper of Georg Frobenius and Ludwig Stickelberger
Ludwig Stickelberger
Ludwig Stickelberger was a Swiss mathematician who made important contributions to linear algebra and algebraic number theory .-Short biography:Stickelberger was born in Buch in the canton of Schaffhausen into a family of a...
and later was both simplified and generalized to finitely generated modules over a principal ideal domain, forming an important chapter of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
Classification
The fundamental theorem of finite abelian groups states that every finite abelian group G can be expressed as the direct sum of cyclic subgroups of primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
-power order. This is a special case of the fundamental theorem of finitely generated abelian groups when G has zero rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
.
The cyclic group
 of order mn is isomorphic to the direct sum of
of order mn is isomorphic to the direct sum of 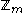 and
and 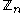 if and only if m and n are coprime
if and only if m and n are coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. It follows that any finite abelian group G is isomorphic to a direct sum of the form

in either of the following canonical ways:
- the numbers k1,...,ku are powers of primes
- k1 dividesDivisorIn mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
k2, which divides k3, and so on up to ku.
For example,
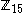 can be expressed as the direct sum of two cyclic subgroups of order 3 and 5:
can be expressed as the direct sum of two cyclic subgroups of order 3 and 5: 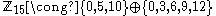 . The same can be said for any abelian group of order 15, leading to the remarkable conclusion that all abelian groups of order 15 are isomorphic
. The same can be said for any abelian group of order 15, leading to the remarkable conclusion that all abelian groups of order 15 are isomorphicGroup isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
.
For another example, every abelian group of order 8 is isomorphic to either
 (the integers 0 to 7 under addition modulo 8),
(the integers 0 to 7 under addition modulo 8), 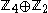 (the odd integers 1 to 15 under multiplication modulo 16), or
(the odd integers 1 to 15 under multiplication modulo 16), or 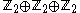 .
.See also list of small groups for finite abelian groups of order 16 or less.
Automorphisms
One can apply the fundamental theorem to count (and sometimes determine) the automorphisms of a given finite abelian group G. To do this, one uses the fact (which will not be proved here) that if G splits as a direct sum H K of subgroups of coprime
K of subgroups of coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
order, then Aut(H
 K)
K) 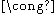 Aut(H)
Aut(H)  Aut(K).
Aut(K).Given this, the fundamental theorem shows that to compute the automorphism group of G it suffices to compute the automorphism groups of the Sylow p-subgroups separately (that is, all direct sums of cyclic subgroups, each with order a power of p). Fix a prime p and suppose the exponents ei of the cyclic factors of the Sylow p-subgroup are arranged in increasing order:

for some n > 0. One needs to find the automorphisms of
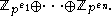
One special case is when n = 1, so that there is only one cyclic prime-power factor in the Sylow p-subgroup P. In this case the theory of automorphisms of a finite cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
can be used. Another special case is when n is arbitrary but ei = 1 for 1 ≤ i ≤ n. Here, one is considering P to be of the form
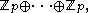
so elements of this subgroup can be viewed as comprising a vector space of dimension n over the finite field of p elements
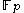 . The automorphisms of this subgroup are therefore given by the invertible linear transformations, so
. The automorphisms of this subgroup are therefore given by the invertible linear transformations, so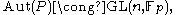
where GL is the appropriate general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
. This is easily shown to have order

In the most general case, where the ei and n are arbitrary, the automorphism group is more difficult to determine. It is known, however, that if one defines
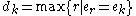
and
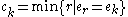
then one has in particular dk ≥ k, ck ≤ k, and

One can check that this yields the orders in the previous examples as special cases (see [Hillar,Rhea]).
Infinite abelian groups
Тhe simplest infinite abelian group is the infinite cyclic group Z. Any finitely generated abelian groupFinitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
A is isomorphic to the direct sum of r copies of Z and a finite abelian group, which in turn is decomposable into a direct sum of finitely many cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of primary orders. Even though the decomposition is not unique, the number r, called the rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
of A, and the prime powers giving the orders of finite cyclic summands are uniquely determined.
By contrast, classification of general infinitely generated abelian groups is far from complete. Divisible group
Divisible group
In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
s, i.e. abelian groups A in which the equation nx = a admits a solution x ∈ A for any natural number n and element a of A, constitute one important class of infinite abelian groups that can be completely characterized. Every divisible group is isomorphic to a direct sum, with summands isomorphic to Q and Prüfer group
Prüfer group
In mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z, for a prime number p is the unique p-group in which every element has p pth roots. The group is named after Heinz Prüfer...
s Qp/Zp for various prime numbers p, and the cardinality of the set of summands of each type is uniquely determined. Moreover, if a divisible group A is a subgroup of an abelian group G then A admits a direct complement: a subgroup C of G such that G = A ⊕ C. Thus divisible groups are injective module
Injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
s in the category of abelian groups, and conversely, every injective abelian group is divisible (Baer's criterion). An abelian group without non-zero divisible subgroups is called reduced.
Two important special classes of infinite abelian groups with diametrically opposite properties are torsion groups and torsion-free groups, examplified by the groups Q/Z (periodic) and Q (torsion-free).
Torsion groups
An abelian group is called periodicPeriodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
or torsion if every element has finite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
. A direct sum of finite cyclic groups is periodic. Although the converse statement is not true in general, some special cases are known. The first and second Prüfer theorems
Prüfer theorems
In mathematics, two Prüfer theorems, named after Heinz Prüfer, describe the structure of certain infinite abelian groups. They have been generalized by L. Ya. Kulikov.- Statement :Let A be an abelian group...
state that if A is a periodic group and either it has bounded exponent, i.e. nA = 0 for some natural number n, or if A is countable and the p-heights
Height (abelian group)
In mathematics, the height of an element g of an abelian group A is an invariant that captures its divisibility properties: it is the largest natural number N such that the equation Nx = g has a solution x ∈ A, or symbol ∞ if the largest number with this property does not exist...
of the elements of A are finite for each p, then A is isomorphic to a direct sum of finite cyclic groups. The cardinality of the set of direct summands isomorphic to Z/pmZ in such a decomposition is an invariant of A. These theorems were later subsumed in the Kulikov criterion. In a different direction, Helmut Ulm
Helmut Ulm
Helmut Ulm was a German mathematician who established the classification of countable periodic abelian groups by means of their Ulm invariants.- Short biography :...
found an extension of the second Prüfer theorem to countable abelian p-groups with elements of infinite height: those groups are completely classified by means of their Ulm invariants.
Torsion-free and mixed groups
An abelian group is called torsion-free if every non-zero element has infinite order. Several classes of torsion-free abelian groups have been extensively studied:- Free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
s, i.e. arbitrary direct sums of Z - CotorsionCotorsion groupIn mathematics, in the realm of abelian group theory, an abelian group is said to be cotorsion if every extension of it by a torsion-free group splits. If the group is C, this is equivalent to asserting that Ext = 0 for all torsion-free groups G...
and algebraically compactAlgebraically compact moduleIn mathematics, especially in the area of abstract algebra known as module theory, algebraically compact modules, also called pure-injective modules, are modules that have a certain "nice" property which allows the solution of infinite systems of equations in the module by finitary means. The...
torsion-free groups such as the p-adic integers - Slender groupSlender groupIn mathematics, a slender group is a torsion-free abelian group that is "small" in a sense that is made precise in the definition below.- Definition :...
s
An abelian group that is neither periodic nor torsion-free is called mixed. If A is an abelian group and T(A) is its torsion subgroup then the factor group A/T(A) is torsion-free. However, in general the torsion subgroup is not a direct summand of A, so the torsion-free factor cannot be realized as a subgroup of A and A is not isomorphic to T(A) ⊕ A/T(A). Thus the theory of mixed groups involves more than simply combining the results about periodic and torsion-free groups.
Invariants and classification
One of the most basic invariants of an infinite abelian group A is its rankRank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
: the cardinality of the maximal linearly independent subset of A. Abelian groups of rank 0 are precisely the periodic groups, while torsion-free abelian groups of rank 1
Torsion-free abelian groups of rank 1
Infinitely generated abelian groups have very complex structure and are far less well understood than finitely generated abelian groups. Even torsion-free abelian groups are vastly more varied in their characteristics than vector spaces...
are necessarily subgroups of Q and can be completely described. More generally, a torsion-free abelian group of finite rank r is a subgroup of Qr. On the other hand, the group of p-adic integers Zp is a torsion-free abelian group of infinite Z-rank and the groups Zpn with different n are non-isomorphic, so this invariant does not even fully capture properties of some familiar groups.
The classification theorems for finitely generated, divisible, countable periodic, and rank 1 torsion-free abelian groups explained above were all obtained before 1950 and form a foundation of the classification of more general infinite abelian groups. Important technical tools used in classification of infinite abelian groups are pure
Pure subgroup
In mathematics, especially in the area of algebra studying the theory of abelian groups, a pure subgroup is a generalization of direct summand. It has found many uses in abelian group theory and related areas.-Definition:...
and basic
Basic subgroup
In abstract algebra, a basic subgroup is a subgroup of an abelian group which is a direct sum of cyclic subgroups and satisfies further technical conditions. This notion was introduced by L. Ya. Kulikov and by László Fuchs in an attempt to formulate classification theory of infinite abelian...
subgroups. Introduction of various invariants of torsion-free abelian groups has been one avenue of further progress. See the books by Irving Kaplansky
Irving Kaplansky
Irving Kaplansky was a Canadian mathematician.-Biography:He was born in Toronto, Ontario, Canada, after his parents emigrated from Poland and attended the University of Toronto as an undergraduate. After receiving his Ph.D...
, László Fuchs, Phillip Griffiths
Phillip Griffiths
Phillip Griffiths is an American mathematician, known for his work in the field of geometry, and in particular for the complex manifold approach to algebraic geometry. He was a major developer in particular of the theory of variation of Hodge structure in Hodge theory and moduli theory.He received...
, and David Arnold, as well as the proceedings of the conferences on Abelian Group Theory published in Lecture Notes in Mathematics for more recent results.
Additive groups of rings
The additive group of a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is an abelian group, but not all abelian groups are additive groups of rings (with nontrivial multiplication). Some important topics in this area of study are:
- Tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
- Corner's results on countable torsion-free groups
- Shelah's work to remove cardinality restrictions
Relation to other mathematical topics
Many large abelian groups possess a natural topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, which turns them into topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s.
The collection of all abelian groups, together with the homomorphisms
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
between them, forms the category
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
Ab, the prototype of an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.
Nearly all well-known algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s other than Boolean algebras, are undecidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
. Hence it is surprising that Tarski's student Szmielew (1955) proved that the first order theory of abelian groups, unlike its nonabelian counterpart, is decidable. This decidability, plus the fundamental theorem of finite abelian groups described above, highlight some of the successes in abelian group theory, but there are still many areas of current research:
- Amongst torsion-free abelian groups of finite rank, only the finitely generated case and the rank 1Torsion-free abelian groups of rank 1Infinitely generated abelian groups have very complex structure and are far less well understood than finitely generated abelian groups. Even torsion-free abelian groups are vastly more varied in their characteristics than vector spaces...
case are well understood; - There are many unsolved problems in the theory of infinite-rank torsion-free abelian groups;
- While countable torsion abelian groups are well understood through simple presentations and Ulm invariants, the case of countable mixed groups is much less mature.
- Many mild extensions of the first order theory of abelian groups are known to be undecidable.
- Finite abelian groups remain a topic of research in computational group theory.
Moreover, abelian groups of infinite order lead, quite surprisingly, to deep questions about the set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
commonly assumed to underlie all of mathematics. Take the Whitehead problem
Whitehead problem
In group theory, a branch of abstract algebra, the Whitehead problem is the following question:Shelah proved that Whitehead's problem is undecidable within standard ZFC set theory.-Refinement:...
: are all Whitehead groups of infinite order also free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
s? In the 1970s, Saharon Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
proved that the Whitehead problem is:
- Undecidable in ZFC, the conventional axiomatic set theory from which nearly all of present day mathematics can be derived. The Whitehead problem is also the first question in ordinary mathematics proved undecidable in ZFC;
- Undecidable even if ZFC is augmented by taking the generalized continuum hypothesis as an axiom;
- Decidable if ZFC is augmented with the axiom of constructibilityConstructible universeIn mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
(see statements true in LStatements true in LHere is a list of propositions that hold in the constructible universe :* The generalized continuum hypothesis and as a consequence** The axiom of choice* Diamondsuit** Clubsuit* Global square* The existence of morasses...
).
A note on the typography
Among mathematical adjectiveAdjective
In grammar, an adjective is a 'describing' word; the main syntactic role of which is to qualify a noun or noun phrase, giving more information about the object signified....
s derived from the proper name
Proper name
"A proper name [is] a word that answers the purpose of showing what thing it is that we are talking about" writes John Stuart Mill in A System of Logic , "but not of telling anything about it"...
of a mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, the word "abelian" is rare in that it is often spelled with a lowercase a, rather than an uppercase A, indicating how ubiquitous the concept is in modern mathematics.
See also
- Abelianization
- Class field theoryClass field theoryIn mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
- Commutator subgroupCommutator subgroupIn mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
- Elementary abelian groupElementary Abelian groupIn group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
- Pontryagin dualityPontryagin dualityIn mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
- Pure injective module
- Pure projective module

