
Prüfer group
Encyclopedia
In mathematics
, specifically in group theory
, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z(p∞), for a prime number
p is the unique p-group
in which every element has p pth roots. The group is named after Heinz Prüfer
. It is a countable
abelian group
which helps taxonomize infinite abelian groups.
The Prüfer p-group may be represented
as a subgroup of the circle group, U(1), as the set of pnth roots of unity
as n ranges over all non-negative integers:
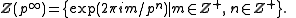
Alternatively, the Prüfer p-group may be seen as the Sylow p-subgroup of Q/Z, consisting of those elements whose order is a power of p: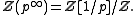
There is a presentation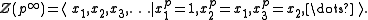
The Prüfer p-group is the unique infinite p-group
which is locally cyclic
(every finite set of elements generates a cyclic group).
The Prüfer p-group is divisible
.
In the language of universal algebra
, an abelian group is subdirectly irreducible if and only if it is isomorphic to a finite cyclic p-group or isomorphic to a Prüfer group.
In the theory of locally compact topological groups the Prüfer p-group (endowed with the discrete topology) is the Pontryagin dual of the compact group of p-adic integers, and the group of p-adic integers is the Pontryagin dual of the Prüfer p-group.
The Prüfer p-groups for all primes p are the only infinite groups whose subgroups are totally ordered by inclusion. As there is no maximal subgroup
of a Prüfer p-group, it is its own Frattini subgroup
.
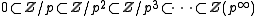
This sequence of inclusions expresses the Prüfer p-group as the direct limit
of its finite subgroups.
As a -module, the Prüfer p-group is Artinian
-module, the Prüfer p-group is Artinian
, but not Noetherian
, and likewise as a group, it is Artinian but not Noetherian. It can thus be used as a counterexample against the idea that every Artinian module is Noetherian (whereas every Artinian ring
is Noetherian).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z(p∞), for a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p is the unique p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
in which every element has p pth roots. The group is named after Heinz Prüfer
Heinz Prüfer
Ernst Paul Heinz Prüfer was a German mathematician, who worked on abelian groups, algebraic numbers, knot theory and Sturm-Liouville theory. His advisor was Issai Schur.- See also :* Prüfer manifold...
. It is a countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
which helps taxonomize infinite abelian groups.
The Prüfer p-group may be represented
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
as a subgroup of the circle group, U(1), as the set of pnth roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
as n ranges over all non-negative integers:
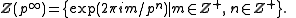
Alternatively, the Prüfer p-group may be seen as the Sylow p-subgroup of Q/Z, consisting of those elements whose order is a power of p:
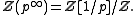
There is a presentation
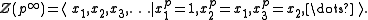
The Prüfer p-group is the unique infinite p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
which is locally cyclic
Locally cyclic group
In group theory, a locally cyclic group is a group in which every finitely generated subgroup is cyclic.-Some facts:*Every cyclic group is locally cyclic, and every locally cyclic group is abelian....
(every finite set of elements generates a cyclic group).
The Prüfer p-group is divisible
Divisible group
In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
.
In the language of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, an abelian group is subdirectly irreducible if and only if it is isomorphic to a finite cyclic p-group or isomorphic to a Prüfer group.
In the theory of locally compact topological groups the Prüfer p-group (endowed with the discrete topology) is the Pontryagin dual of the compact group of p-adic integers, and the group of p-adic integers is the Pontryagin dual of the Prüfer p-group.
The Prüfer p-groups for all primes p are the only infinite groups whose subgroups are totally ordered by inclusion. As there is no maximal subgroup
Maximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
of a Prüfer p-group, it is its own Frattini subgroup
Frattini subgroup
In mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
.
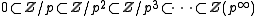
This sequence of inclusions expresses the Prüfer p-group as the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of its finite subgroups.
As a
 -module, the Prüfer p-group is Artinian
-module, the Prüfer p-group is ArtinianArtinian module
In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
, but not Noetherian
Noetherian module
In abstract algebra, an Noetherian module is a module that satisfies the ascending chain condition on its submodules, where the submodules are partially ordered by inclusion....
, and likewise as a group, it is Artinian but not Noetherian. It can thus be used as a counterexample against the idea that every Artinian module is Noetherian (whereas every Artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
is Noetherian).
See also
- p-adic integers, which can be defined as the inverse limitInverse limitIn mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the finite subgroups of the Prüfer p-group. - Dyadic rationalDyadic rationalIn mathematics, a dyadic fraction or dyadic rational is a rational number whose denominator is a power of two, i.e., a number of the form a/2b where a is an integer and b is a natural number; for example, 1/2 or 3/8, but not 1/3...
, rational numbers of the form a/2b. The Prüfer 2-group can be viewed as the dyadic rationals modulo 1.

