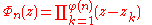Root of unity
Encyclopedia
In mathematics
, a root of unity, or de Moivre
number, is any complex number
that equals 1 when raised
to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory
, the theory of group characters, field theory
, and the discrete Fourier transform
.
The notion of root of unity also applies to any algebraic ring
with a multiplicative identity element
, namely a root of unity is any element of finite multiplicative order
.
z satisfying the equation
An nth root of unity is primitive if it is not a kth root of unity for some smaller k:
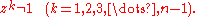
If z is an nth root of unity and a ≡ b (mod n) then za = zb. By the definition of congruence, a = b + kn for some integer k. But then,
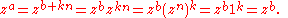
Therefore, given a power za of z, it can be assumed that 1 ≤ a ≤ n. This is often convenient.
Any integer power of an nth root of unity is also an nth root of unity:
Here k may be negative. In particular, the reciprocal of an nth root of unity is its complex conjugate
, and is also an nth root of unity:
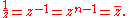
Let z be a primitive nth root of unity. Then the powers z, z2, ... zn−1, zn = z0 = 1 are all distinct. Assume the contrary, that za = zb where 1 ≤ a < b ≤ n. Then zb−a = 1. But 0 < b−a < n, which contradicts z being primitive.
Since an nth degree polynomial equation can only have n distinct roots, this implies that the powers of a primitive root z, z2, ... zn−1, zn = z0 = 1 are in fact all of the nth roots of unity.
From the preceding facts it follows that if z is a primitive nth root of unity:
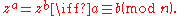
If z is not primitive there is only one implication:
An example showing that the converse implication is false is given by:
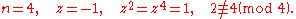
Let z be a primitive nth root of unity and let k be a positive integer. From the above discussion, zk is a primitive root of unity for some a. Now if zka = 1, ka must be a multiple of n. The smallest number that is divisible by both n and k is their least common multiple
, denoted by lcm(n, k). It is related to their greatest common divisor
, gcd(n, k), by the formula:
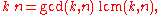
i.e.
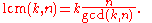
Therefore, zk is a primitive ath root of unity where
Thus, if k and n are coprime
zk is also a primitive nth root of unity, and therefore there are φ(n) (where φ is Euler's totient function
) distinct primitive nth roots of unity. (This implies that if n is a prime number, all the roots except +1 are primitive).
In other words, if R(n) is the set of all nth roots of unity and P(n) is the set of primitive ones, R(n) is a disjoint union of the P(n):
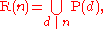
where the notation means that d goes through all the divisors of n, including 1 and n.
Since the cardinality of R(n) is n, and that of P(n) is φ(n), this demonstrates the classical formula
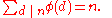
de Moivre's formula
, which is valid for all real x and integers n, is
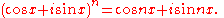
Setting x = 2π/n gives a primitive nth root of unity:
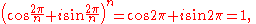
but for k = 1, 2, ... n−1,
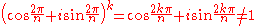
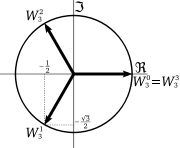
This formula shows that on the complex plane
the nth roots of unity are at the vertices of a regular n-sided polygon
inscribed in the unit circle
, with one vertex at 1. (See the plots for n = 3 and n = 5 on the right). This geometric fact accounts for the term "cyclotomic" in such phrases as cyclotomic field
and cyclotomic polynomial
; it is from the Greek roots "cyclo" (circle) plus "tomos" (cut, divide).
Euler's formula
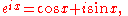
which is valid for all real x, can be used to put the formula for the nth roots of unity into its most familiar form
It follows from the discussion in the previous section that this is a primitive root if and only if the fraction k/n is in lowest terms, i.e. that k and n are coprime.
The roots of unity are, by definition, the roots of a polynomial equation and are thus algebraic number
s. In fact, Galois theory
can be used to show that they may be expressed as expressions involving integers and the operations of addition, subtraction, multiplication, division, and the extraction of roots. (There are more details later in this article at Cyclotomic fields.)
The equation z1 = 1 obviously has only one solution, +1, which is therefore the only primitive first root of unity. It is a nonprimitive 2nd, 3rd, 4th, ... root of unity.
The equation z2 = 1 has two solutions, +1 and −1. +1 is the primitive first root of unity, leaving −1 as the only primitive second (square) root of unity. It is a nonprimitive 4th, 6th, 8th, ...root of unity.
The only real roots of unity are ±1; all the others are non-real complex numbers, as can be seen from de Moivre's formula or the figures.
The third (cube) roots satisfy the equation z3 − 1 = 0; the non-principal root +1 may be factored out, giving (z − 1)(z2 + z + 1) = 0. Therefore, the primitive cube roots of unity are the roots of a quadratic equation. (See Cyclotomic polynomial, below.)
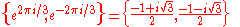
The two primitive fourth roots of unity are the two square roots of the primitive square root of unity, −1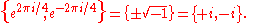
The four primitive fifth roots of unity are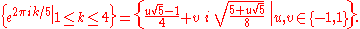
The two primitive sixth roots of unity are the negatives (and also the square roots) of the two primitive cube roots: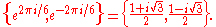
Gauss observed that if a primitive nth root of unity can be expressed using only square roots, then it is possible to construct the regular n-gon using only ruler and compass, and that if the root of unity requires third or fourth or higher radicals the regular polygon cannot be constructed. The 7th roots of unity are the first that require cube roots. Note that the real part and imaginary part are both real numbers, but complex numbers are buried in the expressions. They cannot be removed. See casus irreducibilis
for details.
One of the primitive seventh roots of unity is
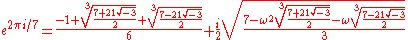
where ω and ω2 are the primitive cube roots of unity exp(2πi/3) and exp(4πi/3).
The four primitive eighth roots of unity are ± the square roots of the primitive fourth roots, ±i. One of them is: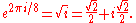
See heptadecagon
for the real part of a 17th root of unity.
is n-periodic (because z j+n = z j·zn = z j·1 = z j for all values of j), and the n sequences of powers
for k = 1, …, n are all n-periodic (because zk·(j+n) = zk·j). Furthermore, the set {s1, …, sn} of these sequences is a basis
of the linear space of all n-periodic sequences. This means that any n-periodic sequence of complex numbers
can be expressed as a linear combination
of powers of a primitive nth root of unity:
for some complex numbers X1, …, Xn and every integer j.
This is a form of Fourier analysis. If j is a (discrete) time variable, then k is a frequency
and Xk is a complex amplitude
.
Choosing for the primitive nth root of unity
allows xj to be expressed as a linear combination of cos and sin:
This is a discrete Fourier transform
.
For n = 1 there is nothing to prove. For n > 1, it is "intuitively obvious" from the symmetry of the roots in the complex plane. For a rigorous proof, let z be a primitive nth root of unity. Then the set of all roots is given by zk, k = 0, 1, ..., n−1, and their sum is given by the formula for a geometric series:
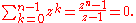
Let SP(n) be the sum of all the primitive nth roots of unity. Then
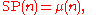
where μ(n) is the Mobius function
.
In the section Elementary facts, it was shown that if R(n) is the set of all nth roots of unity and P(n) is the set of primitive ones, R(n) is a disjoint union of the P(n):
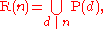
This implies
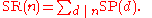
Applying the Mobius inversion formula
gives
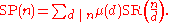
In this formula, if d < n SR(n/d) = 0, and for d = n, SR(n/d) = 1. Therefore, SP(n) = μ(n).
This is the special case cn(1) of Ramanujan's sum cn(s), defined as the sum of the sth powers of the primitive nth roots of unity:
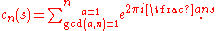
relationship: for j = 1, ···, n and j ' = 1, ···, n
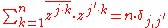
where
is the Kronecker delta and z is any primitive nth root of unity.
The
matrix
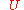whose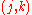 
th entry is
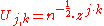
defines a discrete Fourier transform
. Computing the inverse transformation using gaussian elimination
requires O(n3) operations. However, it follows from the orthogonality that U is unitary. That is,
and thus the inverse of U is simply the complex conjugate. (This fact was first noted by Gauss
when solving the problem of trigonometric interpolation
). The straightforward application of U or its inverse to a given vector requires O(n2) operations. The fast Fourier transform
algorithms reduces the number of operations further to O(n log n).
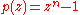
are precisely the nth roots of unity, each with multiplicity 1. The nth cyclotomic polynomial
is defined by the fact that its zeros are precisely the primitive nth roots of unity, each with multiplicity 1.
where z1,z2,z3,...,zφ(n) are the primitive nth roots of unity, and φ(n) is Euler's totient function
. The polynomial Φn(z) has integer coefficients and is an irreducible polynomial
over the rational number
s (i.e., it cannot be written as the product of two positive-degree polynomials with rational coefficients). The case of prime n, which is easier than the general assertion, follows by applying Eisenstein's criterion
to the polynomial ((z + 1)n−1) / ((z + 1) − 1), and expanding via the binomial theorem.
Every nth root of unity is a primitive dth root of unity for exactly one positive divisor
d of n. This implies that
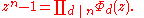
This formula represents the factorization of the polynomial zn − 1 into irreducible factors.
Applying Möbius inversion to the formula gives
where μ is the Möbius function
.
So the first few cyclotomic polynomials are
Φ2( z) = (z2−1)·(z−1)−1 = z+1
Φ3( z) = (z3−1)·(z−1)−1 = z2+z+1
Φ4( z) = (z4−1)·(z2−1)−1 = z2+1
Φ5( z) = (z5−1)·(z−1)−1 = z4+z3+z2+z+1
Φ6( z) = (z6−1)·(z3−1)−1·(z2−1)−1·(z−1) = z2−z+1
Φ7( z) = (z7−1)·(z−1)−1 = z6+z5+z4+z3+z2+z+1
If p is a prime number
, then all the pth roots of unity except 1 are primitive pth roots, and we have
Substituting any positive integer ≥ 2 for z, this sum becomes a base z repunit
. Thus a necessary (but not sufficient) condition for a repunit to be prime is that its length be prime.
Note that, contrary to first appearances, not all coefficients of all cyclotomic polynomials are 0, 1, or −1. The first exception is Φ105. It is not a surprise it takes this long to get an example, because the behavior of the coefficients depends not so much on n as on how many odd prime factors appear in n. More precisely, it can be shown that if n has 1 or 2 odd prime factors (e.g., n = 150) then the nth cyclotomic polynomial only has coefficients 0, 1 or −1. Thus the first conceivable n for which there could be a coefficient besides 0, 1, or −1 is a product of the three smallest odd primes, and that is 3·5·7 = 105. This by itself doesn't prove the 105th polynomial has another coefficient, but does show it is the first one which even has a chance of working (and then a computation of the coefficients shows it does). A theorem of Schur says that there are cyclotomic polynomials with coefficients arbitrarily large in absolute value. In particular, if where are odd primes, and t is odd, then 1 − t occurs as a coefficient in the nth cyclotomic polynomial.
Many restrictions are known about the values that cyclotomic polynomials can assume at integer values. For example, if p is prime and d | Φp(d), then either d ≡ 1 mod (p), or d ≡ 0 mod (p).
Cyclotomic polynomials are solvable in radical
s, as roots of unity are themselves radicals. Moreover, there exist more informative radical expressions for nth roots of unity with the additional property that every value of the expression obtained by choosing values of the radicals (for example, signs of square roots) is a primitive nth root of unity. This was already shown by Gauss
in 1797. Efficient algorithm
s exist for calculating such expressions.
of order
n, and in fact these groups comprise all of the finite subgroups of the multiplicative group
of the complex number field. A generator
for this cyclic group is a primitive nth root of unity.
The nth roots of unity form an irreducible representation
of any cyclic group of order n. The orthogonality relationship also follows from group-theoretic principles as described in character group
.
The roots of unity appear as entries of the eigenvectors of any circulant matrix
, i.e. matrices that are invariant under cyclic shifts, a fact that also follows from group representation theory as a variant of Bloch's theorem
. In particular, if a circulant Hermitian matrix is considered (for example, a discretized one-dimensional Laplacian with periodic boundaries), the orthogonality property immediately follows from the usual orthogonality of eigenvectors of Hermitian matrices.
Fn. This field
contains all nth roots of unity and is the splitting field
of the nth cyclotomic polynomial over Q. The field extension
Fn/Q has degree φ(n) and its Galois group
is naturally
isomorphic
to the multiplicative group of units of the ring Z/nZ.
As the Galois group of Fn/Q is abelian, this is an abelian extension
. Every subfield of a cyclotomic field is an abelian extension of the rationals. In these cases Galois theory
can be written out explicitly in terms of Gaussian period
s: this theory from the Disquisitiones Arithmeticae
of Gauss
was published many years before Galois.
Conversely, every abelian extension of the rationals is such a subfield of a cyclotomic field — this is the content of a theorem of Kronecker
, usually called the Kronecker–Weber theorem
on the grounds that Weber completed the proof.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a root of unity, or de Moivre
Abraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
number, is any complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
that equals 1 when raised
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the theory of group characters, field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, and the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
.
The notion of root of unity also applies to any algebraic ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
with a multiplicative identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, namely a root of unity is any element of finite multiplicative order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
.
Definition
An nth root of unity, where n = 1,2,3,··· is a positive integer, is a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
z satisfying the equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
An nth root of unity is primitive if it is not a kth root of unity for some smaller k:
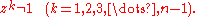
Elementary facts
Every nth root of unity z is a primitive ath root of unity for some a where 1 ≤ a ≤ n: if z1 = 1 then z is a primitive first root of unity, otherwise if z2 = 1 then z is a primitive second (square) root of unity, otherwise, ..., and by assumption there must be a "1" at or before the nth term in the sequence.If z is an nth root of unity and a ≡ b (mod n) then za = zb. By the definition of congruence, a = b + kn for some integer k. But then,
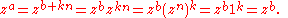
Therefore, given a power za of z, it can be assumed that 1 ≤ a ≤ n. This is often convenient.
Any integer power of an nth root of unity is also an nth root of unity:
Here k may be negative. In particular, the reciprocal of an nth root of unity is its complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
, and is also an nth root of unity:
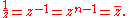
Let z be a primitive nth root of unity. Then the powers z, z2, ... zn−1, zn = z0 = 1 are all distinct. Assume the contrary, that za = zb where 1 ≤ a < b ≤ n. Then zb−a = 1. But 0 < b−a < n, which contradicts z being primitive.
Since an nth degree polynomial equation can only have n distinct roots, this implies that the powers of a primitive root z, z2, ... zn−1, zn = z0 = 1 are in fact all of the nth roots of unity.
From the preceding facts it follows that if z is a primitive nth root of unity:
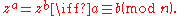
If z is not primitive there is only one implication:
An example showing that the converse implication is false is given by:
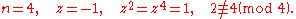
Let z be a primitive nth root of unity and let k be a positive integer. From the above discussion, zk is a primitive root of unity for some a. Now if zka = 1, ka must be a multiple of n. The smallest number that is divisible by both n and k is their least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
, denoted by lcm(n, k). It is related to their greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
, gcd(n, k), by the formula:
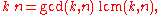
i.e.
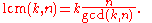
Therefore, zk is a primitive ath root of unity where
Thus, if k and n are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
zk is also a primitive nth root of unity, and therefore there are φ(n) (where φ is Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
) distinct primitive nth roots of unity. (This implies that if n is a prime number, all the roots except +1 are primitive).
In other words, if R(n) is the set of all nth roots of unity and P(n) is the set of primitive ones, R(n) is a disjoint union of the P(n):
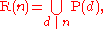
where the notation means that d goes through all the divisors of n, including 1 and n.
Since the cardinality of R(n) is n, and that of P(n) is φ(n), this demonstrates the classical formula
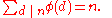
Examples
De Moivre's formula
In mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any complex number x and integer n it holds that...
, which is valid for all real x and integers n, is
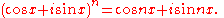
Setting x = 2π/n gives a primitive nth root of unity:
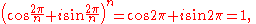
but for k = 1, 2, ... n−1,
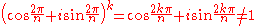
This formula shows that on the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
the nth roots of unity are at the vertices of a regular n-sided polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
inscribed in the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, with one vertex at 1. (See the plots for n = 3 and n = 5 on the right). This geometric fact accounts for the term "cyclotomic" in such phrases as cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
and cyclotomic polynomial
Cyclotomic polynomial
In algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
; it is from the Greek roots "cyclo" (circle) plus "tomos" (cut, divide).
Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
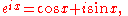
which is valid for all real x, can be used to put the formula for the nth roots of unity into its most familiar form
It follows from the discussion in the previous section that this is a primitive root if and only if the fraction k/n is in lowest terms, i.e. that k and n are coprime.
The roots of unity are, by definition, the roots of a polynomial equation and are thus algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s. In fact, Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
can be used to show that they may be expressed as expressions involving integers and the operations of addition, subtraction, multiplication, division, and the extraction of roots. (There are more details later in this article at Cyclotomic fields.)
The equation z1 = 1 obviously has only one solution, +1, which is therefore the only primitive first root of unity. It is a nonprimitive 2nd, 3rd, 4th, ... root of unity.
The equation z2 = 1 has two solutions, +1 and −1. +1 is the primitive first root of unity, leaving −1 as the only primitive second (square) root of unity. It is a nonprimitive 4th, 6th, 8th, ...root of unity.
The only real roots of unity are ±1; all the others are non-real complex numbers, as can be seen from de Moivre's formula or the figures.
The third (cube) roots satisfy the equation z3 − 1 = 0; the non-principal root +1 may be factored out, giving (z − 1)(z2 + z + 1) = 0. Therefore, the primitive cube roots of unity are the roots of a quadratic equation. (See Cyclotomic polynomial, below.)
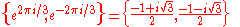
The two primitive fourth roots of unity are the two square roots of the primitive square root of unity, −1
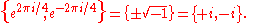
The four primitive fifth roots of unity are
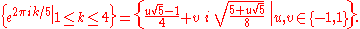
The two primitive sixth roots of unity are the negatives (and also the square roots) of the two primitive cube roots:
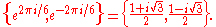
Gauss observed that if a primitive nth root of unity can be expressed using only square roots, then it is possible to construct the regular n-gon using only ruler and compass, and that if the root of unity requires third or fourth or higher radicals the regular polygon cannot be constructed. The 7th roots of unity are the first that require cube roots. Note that the real part and imaginary part are both real numbers, but complex numbers are buried in the expressions. They cannot be removed. See casus irreducibilis
Casus irreducibilis
In algebra, casus irreducibilis is one of the cases that may arise in attempting to solve a cubic equation with integer coefficients with roots that are expressed with radicals...
for details.
One of the primitive seventh roots of unity is
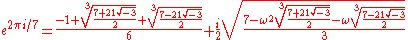
where ω and ω2 are the primitive cube roots of unity exp(2πi/3) and exp(4πi/3).
The four primitive eighth roots of unity are ± the square roots of the primitive fourth roots, ±i. One of them is:
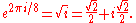
See heptadecagon
Heptadecagon
In geometry, a heptadecagon is a seventeen-sided polygon.-Heptadecagon construction:The regular heptadecagon is a constructible polygon, as was shown by Carl Friedrich Gauss in 1796 at the age of 19....
for the real part of a 17th root of unity.
Periodicity
If z is a primitive nth root of unity, then the sequence of powers- …,
is n-periodic (because z j+n = z j·zn = z j·1 = z j for all values of j), and the n sequences of powers
for k = 1, …, n are all n-periodic (because zk·(j+n) = zk·j). Furthermore, the set {s1, …, sn} of these sequences is a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the linear space of all n-periodic sequences. This means that any n-periodic sequence of complex numbers
- …,
can be expressed as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of powers of a primitive nth root of unity:
for some complex numbers X1, …, Xn and every integer j.
This is a form of Fourier analysis. If j is a (discrete) time variable, then k is a frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
and Xk is a complex amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
.
Choosing for the primitive nth root of unity
allows xj to be expressed as a linear combination of cos and sin:
This is a discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
.
Summation
Let SR(n) be the sum of all the nth roots of unity, primitive or not. ThenFor n = 1 there is nothing to prove. For n > 1, it is "intuitively obvious" from the symmetry of the roots in the complex plane. For a rigorous proof, let z be a primitive nth root of unity. Then the set of all roots is given by zk, k = 0, 1, ..., n−1, and their sum is given by the formula for a geometric series:
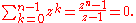
Let SP(n) be the sum of all the primitive nth roots of unity. Then
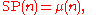
where μ(n) is the Mobius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
In the section Elementary facts, it was shown that if R(n) is the set of all nth roots of unity and P(n) is the set of primitive ones, R(n) is a disjoint union of the P(n):
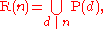
This implies
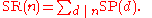
Applying the Mobius inversion formula
Möbius inversion formula
In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
gives
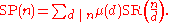
In this formula, if d < n SR(n/d) = 0, and for d = n, SR(n/d) = 1. Therefore, SP(n) = μ(n).
This is the special case cn(1) of Ramanujan's sum cn(s), defined as the sum of the sth powers of the primitive nth roots of unity:
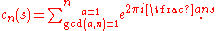
Orthogonality
From the summation formula follows an orthogonalityOrthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
relationship: for j = 1, ···, n and j ' = 1, ···, n
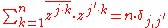
where
is the Kronecker delta and z is any primitive nth root of unity.The
matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
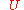whose 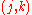th entry is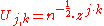defines a discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
. Computing the inverse transformation using gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
requires O(n3) operations. However, it follows from the orthogonality that U is unitary. That is,
and thus the inverse of U is simply the complex conjugate. (This fact was first noted by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
when solving the problem of trigonometric interpolation
Trigonometric interpolation
In mathematics, trigonometric interpolation is interpolation with trigonometric polynomials. Interpolation is the process of finding a function which goes through some given data points. For trigonometric interpolation, this function has to be a trigonometric polynomial, that is, a sum of sines and...
). The straightforward application of U or its inverse to a given vector requires O(n2) operations. The fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
algorithms reduces the number of operations further to O(n log n).
Cyclotomic polynomials
The zeroes of the polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
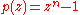
are precisely the nth roots of unity, each with multiplicity 1. The nth cyclotomic polynomial
Cyclotomic polynomial
In algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
is defined by the fact that its zeros are precisely the primitive nth roots of unity, each with multiplicity 1.
where z1,z2,z3,...,zφ(n) are the primitive nth roots of unity, and φ(n) is Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
. The polynomial Φn(z) has integer coefficients and is an irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s (i.e., it cannot be written as the product of two positive-degree polynomials with rational coefficients). The case of prime n, which is easier than the general assertion, follows by applying Eisenstein's criterion
Eisenstein's criterion
In mathematics, Eisenstein's criterion gives an easily checked sufficient condition for a polynomial with integer coefficients to be irreducible over the rational numbers...
to the polynomial ((z + 1)n−1) / ((z + 1) − 1), and expanding via the binomial theorem.
Every nth root of unity is a primitive dth root of unity for exactly one positive divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
d of n. This implies that
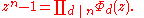
This formula represents the factorization of the polynomial zn − 1 into irreducible factors.
Applying Möbius inversion to the formula gives
where μ is the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
So the first few cyclotomic polynomials are
- Φ1(
If p is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, then all the pth roots of unity except 1 are primitive pth roots, and we have
Substituting any positive integer ≥ 2 for z, this sum becomes a base z repunit
Repunit
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1. The term stands for repeated unit and was coined in 1966 by Albert H. Beiler...
. Thus a necessary (but not sufficient) condition for a repunit to be prime is that its length be prime.
Note that, contrary to first appearances, not all coefficients of all cyclotomic polynomials are 0, 1, or −1. The first exception is Φ105. It is not a surprise it takes this long to get an example, because the behavior of the coefficients depends not so much on n as on how many odd prime factors appear in n. More precisely, it can be shown that if n has 1 or 2 odd prime factors (e.g., n = 150) then the nth cyclotomic polynomial only has coefficients 0, 1 or −1. Thus the first conceivable n for which there could be a coefficient besides 0, 1, or −1 is a product of the three smallest odd primes, and that is 3·5·7 = 105. This by itself doesn't prove the 105th polynomial has another coefficient, but does show it is the first one which even has a chance of working (and then a computation of the coefficients shows it does). A theorem of Schur says that there are cyclotomic polynomials with coefficients arbitrarily large in absolute value. In particular, if where are odd primes, and t is odd, then 1 − t occurs as a coefficient in the nth cyclotomic polynomial.
Many restrictions are known about the values that cyclotomic polynomials can assume at integer values. For example, if p is prime and d | Φp(d), then either d ≡ 1 mod (p), or d ≡ 0 mod (p).
Cyclotomic polynomials are solvable in radical
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
s, as roots of unity are themselves radicals. Moreover, there exist more informative radical expressions for nth roots of unity with the additional property that every value of the expression obtained by choosing values of the radicals (for example, signs of square roots) is a primitive nth root of unity. This was already shown by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in 1797. Efficient algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s exist for calculating such expressions.
Cyclic groups
The nth roots of unity form under multiplication a cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
n, and in fact these groups comprise all of the finite subgroups of the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of the complex number field. A generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
for this cyclic group is a primitive nth root of unity.
The nth roots of unity form an irreducible representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of any cyclic group of order n. The orthogonality relationship also follows from group-theoretic principles as described in character group
Character group
In mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory...
.
The roots of unity appear as entries of the eigenvectors of any circulant matrix
Circulant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
, i.e. matrices that are invariant under cyclic shifts, a fact that also follows from group representation theory as a variant of Bloch's theorem
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
. In particular, if a circulant Hermitian matrix is considered (for example, a discretized one-dimensional Laplacian with periodic boundaries), the orthogonality property immediately follows from the usual orthogonality of eigenvectors of Hermitian matrices.
Cyclotomic fields
By adjoining a primitive nth root of unity to Q, one obtains the nth cyclotomic fieldCyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
Fn. This field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
contains all nth roots of unity and is the splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of the nth cyclotomic polynomial over Q. The field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
Fn/Q has degree φ(n) and its Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
is naturally
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the multiplicative group of units of the ring Z/nZ.
As the Galois group of Fn/Q is abelian, this is an abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
. Every subfield of a cyclotomic field is an abelian extension of the rationals. In these cases Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
can be written out explicitly in terms of Gaussian period
Gaussian period
In mathematics, in the area of number theory, a Gaussian period is a certain kind of sum of roots of unity. The periods permit explicit calculations in cyclotomic fields connected with Galois theory and with harmonic analysis . They are basic in the classical theory called cyclotomy...
s: this theory from the Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
of Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
was published many years before Galois.
Conversely, every abelian extension of the rationals is such a subfield of a cyclotomic field — this is the content of a theorem of Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
, usually called the Kronecker–Weber theorem
Kronecker–Weber theorem
In algebraic number theory, the Kronecker–Weber theorem states that every finite abelian extension of the field of rational numbers Q, or in other words, every algebraic number field whose Galois group over Q is abelian, is a subfield of a cyclotomic field, i.e. a field obtained by adjoining a root...
on the grounds that Weber completed the proof.
See also
- Circle group
- Group scheme of roots of unity
- Primitive root modulo nPrimitive root modulo nIn modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
- Root of unity modulo n
- Dirichlet characterDirichlet characterIn number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
- Ramanujan's sum