
Kronecker–Weber theorem
Encyclopedia
In algebraic number theory
, the Kronecker–Weber theorem states that every finite abelian extension
of the field of rational number
s Q, or in other words, every algebraic number field
whose Galois group
over Q is abelian, is a subfield of a cyclotomic field
, i.e. a field obtained by adjoining a root of unity
to the rational numbers. The theorem was first stated by though his argument was not complete for extensions of degree a power of 2.
published a proof, but this had some gaps and errors that were pointed out and corrected by . The first complete proof was given by .
The Kronecker–Weber theorem can be restated concretely without reference to number fields. If an algebraic integer has abelian Galois group then it is expressible as a finite sum of roots of unity. For example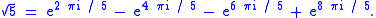
For a given abelian extension K of Q there is a minimal cyclotomic field that contains it. The theorem allows one to define the conductor of K as the smallest integer n such that K lies inside the field generated by the n-th roots of unity. For example the quadratic field
s have as conductor the absolute value of their discriminant
, a fact generalised in class field theory.
can be constructed using cyclotomic extensions and Lubin–Tate extensions. , and gave other proofs.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, the Kronecker–Weber theorem states that every finite abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
of the field of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q, or in other words, every algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
whose Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
over Q is abelian, is a subfield of a cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
, i.e. a field obtained by adjoining a root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
to the rational numbers. The theorem was first stated by though his argument was not complete for extensions of degree a power of 2.
published a proof, but this had some gaps and errors that were pointed out and corrected by . The first complete proof was given by .
The Kronecker–Weber theorem can be restated concretely without reference to number fields. If an algebraic integer has abelian Galois group then it is expressible as a finite sum of roots of unity. For example
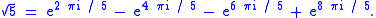
For a given abelian extension K of Q there is a minimal cyclotomic field that contains it. The theorem allows one to define the conductor of K as the smallest integer n such that K lies inside the field generated by the n-th roots of unity. For example the quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
s have as conductor the absolute value of their discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
, a fact generalised in class field theory.
Local Kronecker–Weber theorem
proved the local Kronecker–Weber theorem which states that any abelian extension of a local fieldLocal field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
can be constructed using cyclotomic extensions and Lubin–Tate extensions. , and gave other proofs.

