Character group
Encyclopedia
In mathematics
, a character group is the group of representation
s of a group
by complex
-valued functions
. These functions can be thought of as one-dimensional matrix
representations and so are special cases of the group characters
which arises in the related context of character theory
. Whenever a group is represented by matrices
, the function defined by the trace of the matrices is called a character; however, these traces do not in general form a group. Some important properties of these one-dimensional characters apply to characters in general:
The primary importance of the character group for finite abelian groups is in number theory
, where it is used to construct Dirichlet characters. The character group of the cyclic group
also appears in the theory of the discrete Fourier transform
. For locally compact abelian groups, the character group (with an assumption of
continuity) is central to Fourier analysis.
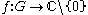mapping the group to the non-zero complex numbers is called a character of G if it is a group homomorphism
—that is, if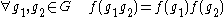
and 
where e is the identity of the group.
If f is a character of a finite group G, then each function value f(g) is a root of unity
(since all elements of a finite group have finite order).
Each character f is a constant on conjugacy class
es of G, that is, f(h g h−1) = f(g). For this reason, the character is sometimes called the class function.
A finite abelian group
of order n has exactly n distinct characters. These are denoted by f1, ..., fn. The function f1 is the trivial representation; that is,
. It is called the principal character of G; the others are called the non-principal characters. The non-principal characters have the property that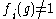 
for some 
.
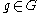for each element 
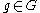. This group is the character group of G and is sometimes denoted as 
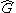. It is of order n. The identity element of 
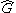is the principal character f1. The inverse of fk is the reciprocal 1/fk. Note that since 
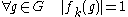, the inverse is equal to the complex conjugate.
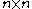matrix A=A(G) whose matrix elements are 
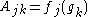where 
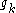is the kth element of G.
The sum of the entries in the jth row of A is given by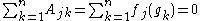
if 
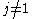, and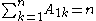
.
The sum of the entries in the kth column of A is given by
if 
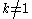, and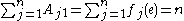
.
Let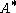
denote the conjugate transpose
of A. Then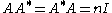
.
This implies the desired orthogonality relationship for the characters: i.e.,
,
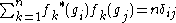where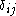
is the Kronecker delta and 
is the complex conjugate of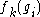 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a character group is the group of representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
by complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. These functions can be thought of as one-dimensional matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
representations and so are special cases of the group characters
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
which arises in the related context of character theory
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
. Whenever a group is represented by matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, the function defined by the trace of the matrices is called a character; however, these traces do not in general form a group. Some important properties of these one-dimensional characters apply to characters in general:
- Characters are invariant on conjugacy classes.
- The characters of irreducible representations are orthogonal.
The primary importance of the character group for finite abelian groups is in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, where it is used to construct Dirichlet characters. The character group of the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
also appears in the theory of the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
. For locally compact abelian groups, the character group (with an assumption of
continuity) is central to Fourier analysis.
Preliminaries
Let G be an abelian group. A function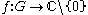 mapping the group to the non-zero complex numbers is called a character of G if it is a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
—that is, if
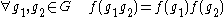and where e is the identity of the group.If f is a character of a finite group G, then each function value f(g) is a root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
(since all elements of a finite group have finite order).
Each character f is a constant on conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es of G, that is, f(h g h−1) = f(g). For this reason, the character is sometimes called the class function.
A finite abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
of order n has exactly n distinct characters. These are denoted by f1, ..., fn. The function f1 is the trivial representation; that is,
. It is called the principal character of G; the others are called the non-principal characters. The non-principal characters have the property that 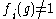for some 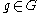.Definition
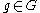If G is an abelian group of order n, then the set of characters fk forms an abelian group under multiplication for each element . This group is the character group of G and is sometimes denoted as 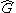. It is of order n. The identity element of 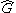is the principal character f1. The inverse of fk is the reciprocal 1/fk. Note that since 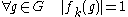, the inverse is equal to the complex conjugate.Orthogonality of characters
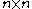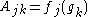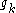Consider the matrix A=A(G) whose matrix elements are where is the kth element of G.The sum of the entries in the jth row of A is given by
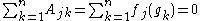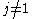if , and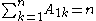.The sum of the entries in the kth column of A is given by
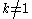if , and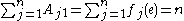.Let
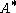denote the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A. Then
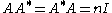.This implies the desired orthogonality relationship for the characters: i.e.,
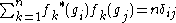,where
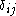is the Kronecker delta and is the complex conjugate of 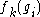.