Irreducible polynomial
Encyclopedia
In mathematics
, the adjective irreducible
means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization
.
For any field
F, the ring
of polynomial
s with coefficients in F is denoted by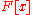
. A polynomial 
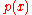in 
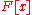is called irreducible over 
if it is non-constant and cannot be represented as the product of two or more non-constant polynomials from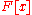 
. The property of irreducibility depends on the field F; a polynomial may be irreducible over some fields but reducible over others. Some simple examples are discussed below.
Galois theory
studies the relationship between a field, its Galois group
, and its irreducible polynomials in depth. Interesting and non-trivial applications can be found in the study of finite field
s.
It is helpful to compare irreducible polynomials to prime number
s: prime numbers (together with the corresponding negative numbers of equal magnitude) are the irreducible integer
s. They exhibit many of the general properties of the concept of 'irreducibility' that equally apply to irreducible polynomials, such as the essentially unique factorization into prime or irreducible factors:
Every polynomial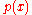
in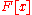 
can be factorized into polynomials that are irreducible over F. This factorization is unique up to
permutation
of the factors and the multiplication of the factors by nonzero constants from F (because the ring of polynomials over a field is a unique factorization domain
whose units are the nonzero constant polynomials).
The set of roots (in an extension field) of any polynomial over F must either contain no roots of a given irreducible polynomial p, or contain all such roots; this is Abel's irreducibility theorem
.
,
,
,
,
.
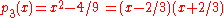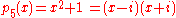Over the ring
of integer
s, the first two polynomials are reducible, the last two are irreducible. (The third, of course, is not a polynomial over the integers.)
Over the field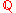
of rational number
s, the first three polynomials are reducible, but the other two polynomials are irreducible.
Over the field
of real number
s, the first four polynomials are reducible, but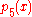
is still irreducible.
Over the field
of complex number
s, all five polynomials are reducible. In fact, every nonzero polynomial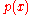
over 
can be factored as
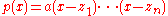
where
is the degree, 
the leading coefficient and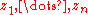 
the zeros of 
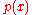. Thus, the only non-constant irreducible polynomials over 
are linear polynomials
. This is the Fundamental theorem of algebra
.
The existence of irreducible polynomials of degree greater than one (without zeros in the original field) historically motivated the extension
of that original number field so that even these polynomials can be reduced into linear factors: from rational number
s (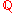
), to the real
subset of the algebraic number
s (
), and finally to the algebraic subset of the complex number
s (
). After the invention of calculus
those latter two subsets were later extended to all real number
s (
) and all complex number
s (
).
For algebraic purposes, the extension from rational numbers to real numbers is too "radical": it introduces transcendental number
s, which are not the solutions of algebraic equations with rational coefficients. These numbers are not needed for the algebraic purpose of factorizing polynomials (but they are necessary for the use of real numbers in analysis
). The set of algebraic numbers (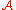
) is the algebraic closure
of the rationals, and contains the roots of all polynomials (including i for instance). This is a countable field and is strictly contained in the complex numbers – the difference being that this field (
) is "algebraically complete" (as are the complexes
,
) but not analytically complete since it lacks the aforementioned transcendentals.
The above paragraph generalizes in that there is a purely algebraic process to extend
a given field F with a given polynomial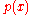
to a larger field where this polynomial 
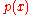can be reduced into linear factors. The study of such extensions is the starting point of Galois theory
.
s are irreducible over the field of complex numbers (this is a consequence of the fundamental theorem of algebra
). Since the complex roots of a real polynomial are in conjugate pairs, the irreducible polynomials over the field of real numbers are the linear polynomials and the quadratic polynomials with no real roots. For example,
factors over the real numbers as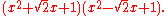 
if there are no non-units g and h with f = gh. One can show that every prime element
is irreducible; the converse is not true in general but holds in unique factorization domain
s. The polynomial ring
F[x] over a field F (or any unique-factorization domain) is again a unique factorization domain. Inductively, this means that the polynomial ring in n indeterminants (over a ring R) is a unique factorization domain if the same is true for R.
behaves similarly to factorization over the rational or the complex field. However, polynomials with integer coefficients that are irreducible over the field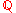
can be reducible over a finite field. For example, the polynomial 
is irreducible over 
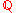but reducible over the field 
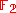of two elements. Indeed, over 
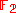, we have
The irreducibility of a polynomial over the integers
is related to that over the field 
of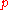 
elements (for a prime 
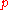). Namely, if a polynomial over 
with leading coefficient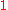 
is reducible over 
then it is reducible over 
for any prime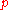 
. The converse, however, is not true.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the adjective irreducible
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
.
For any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with coefficients in F is denoted by
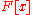. A polynomial 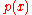in 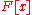is called irreducible over if it is non-constant and cannot be represented as the product of two or more non-constant polynomials from 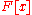. The property of irreducibility depends on the field F; a polynomial may be irreducible over some fields but reducible over others. Some simple examples are discussed below.Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
studies the relationship between a field, its Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
, and its irreducible polynomials in depth. Interesting and non-trivial applications can be found in the study of finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
It is helpful to compare irreducible polynomials to prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s: prime numbers (together with the corresponding negative numbers of equal magnitude) are the irreducible integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. They exhibit many of the general properties of the concept of 'irreducibility' that equally apply to irreducible polynomials, such as the essentially unique factorization into prime or irreducible factors:
Every polynomial
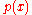in 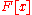can be factorized into polynomials that are irreducible over F. This factorization is unique up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the factors and the multiplication of the factors by nonzero constants from F (because the ring of polynomials over a field is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
whose units are the nonzero constant polynomials).
The set of roots (in an extension field) of any polynomial over F must either contain no roots of a given irreducible polynomial p, or contain all such roots; this is Abel's irreducibility theorem
Abel's irreducibility theorem
In mathematics, Abel's irreducibility theorem, a field theory result described in 1829 by Niels Henrik Abel, asserts that if ƒ is a polynomial over the a field F that shares a root with an irreducible polynomial g, then ƒ is divisible evenly by g In mathematics, Abel's irreducibility...
.
Simple examples
The following five polynomials demonstrate some elementary properties of reducible and irreducible polynomials:,,,,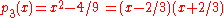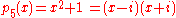.Over the ring
of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, the first two polynomials are reducible, the last two are irreducible. (The third, of course, is not a polynomial over the integers.)
Over the field
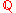of rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, the first three polynomials are reducible, but the other two polynomials are irreducible.
Over the field
of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, the first four polynomials are reducible, but
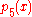is still irreducible.Over the field
of complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, all five polynomials are reducible. In fact, every nonzero polynomial
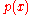over can be factored as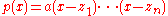where
is the degree, the leading coefficient and 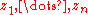the zeros of 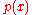. Thus, the only non-constant irreducible polynomials over are linear polynomialsLinear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
. This is the Fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
.
The existence of irreducible polynomials of degree greater than one (without zeros in the original field) historically motivated the extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of that original number field so that even these polynomials can be reduced into linear factors: from rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s (
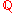), to the realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
subset of the algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s (
), and finally to the algebraic subset of the complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (
). After the invention of calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
those latter two subsets were later extended to all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (
) and all complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (
).For algebraic purposes, the extension from rational numbers to real numbers is too "radical": it introduces transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s, which are not the solutions of algebraic equations with rational coefficients. These numbers are not needed for the algebraic purpose of factorizing polynomials (but they are necessary for the use of real numbers in analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
). The set of algebraic numbers (
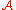) is the algebraic closureAlgebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the rationals, and contains the roots of all polynomials (including i for instance). This is a countable field and is strictly contained in the complex numbers – the difference being that this field (
) is "algebraically complete" (as are the complexesComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
,
) but not analytically complete since it lacks the aforementioned transcendentals.The above paragraph generalizes in that there is a purely algebraic process to extend
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
a given field F with a given polynomial
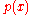to a larger field where this polynomial 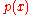can be reduced into linear factors. The study of such extensions is the starting point of Galois theoryGalois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
.
Real and complex numbers
As shown in the examples above, only linear polynomialLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
s are irreducible over the field of complex numbers (this is a consequence of the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
). Since the complex roots of a real polynomial are in conjugate pairs, the irreducible polynomials over the field of real numbers are the linear polynomials and the quadratic polynomials with no real roots. For example,
factors over the real numbers as 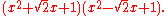Generalization
If R is an integral domain, an element f of R which is neither zero nor a unit is called irreducibleIrreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
if there are no non-units g and h with f = gh. One can show that every prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
is irreducible; the converse is not true in general but holds in unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s. The polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
F[x] over a field F (or any unique-factorization domain) is again a unique factorization domain. Inductively, this means that the polynomial ring in n indeterminants (over a ring R) is a unique factorization domain if the same is true for R.
Finite fields
Factorization over a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
behaves similarly to factorization over the rational or the complex field. However, polynomials with integer coefficients that are irreducible over the field
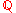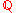can be reducible over a finite field. For example, the polynomial is irreducible over but reducible over the field 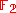of two elements. Indeed, over 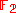, we haveThe irreducibility of a polynomial over the integers
is related to that over the field of 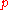elements (for a prime 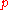). Namely, if a polynomial over with leading coefficient 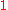is reducible over then it is reducible over for any prime 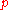. The converse, however, is not true.See also
- Gauss's lemma (polynomial)Gauss's lemma (polynomial)In algebra, in the theory of polynomials , Gauss's lemma is either of two related statements about polynomials with integer coefficients:...
- Rational root theorem
- Eisenstein's criterionEisenstein's criterionIn mathematics, Eisenstein's criterion gives an easily checked sufficient condition for a polynomial with integer coefficients to be irreducible over the rational numbers...
- Hilbert's irreducibility theoremHilbert's irreducibility theoremIn number theory, Hilbert's irreducibility theorem, conceived by David Hilbert, states that every finite number of irreducible polynomials in a finite number of variables and having rational number coefficients admit a common specialization of a proper subset of the variables to rational numbers...
- Cohn's irreducibility criterion
- Irreducible componentIrreducible componentIn mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equationis the union of the two linesandThe notion of irreducibility is stronger than connectedness.- Definition :...
of a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion... - Factorization of polynomial over finite field and irreducibility tests
External links
- Information on Primitive and Irreducible Polynomials, The (Combinatorial) Object Server.