
Prime element
Encyclopedia
In abstract algebra
, an element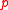 of a commutative ring
of a commutative ring
 is said to be prime if it is not zero, not a unit
is said to be prime if it is not zero, not a unit
and whenever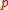 divides
divides
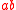 for some
for some  and
and 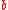 in
in  , then
, then 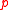 divides
divides  or
or 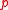 divides
divides  . Equivalently, an element
. Equivalently, an element 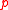 is prime if, and only if, the principal ideal
is prime if, and only if, the principal ideal
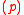 generated by
generated by 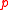 is a nonzero prime ideal
is a nonzero prime ideal
.
Interest in prime elements comes from the Fundamental theorem of arithmetic
, which asserts that each integer
can be written in essentially only one way as 1 or −1 multiplied by a product of positive prime number
s. This led to the study of unique factorization domain
s, which generalize what was just illustrated in the integers.
Prime elements should not be confused with irreducible element
s. In an integral domain, every prime is irreducible but the converse is not true in general. However, in unique factorization domains, or more generally in GCD domain
s, primes and irreducibles are the same.
Being prime is also relative to which ring an element is considered to be in; for example, 2 is a prime element in Z but it is not in Z[ ], the ring of Gaussian integers, since
], the ring of Gaussian integers, since 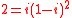 and 2 does not divide any factor on the right.
and 2 does not divide any factor on the right.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an element
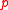 of a commutative ring
of a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
 is said to be prime if it is not zero, not a unit
is said to be prime if it is not zero, not a unitUnit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
and whenever
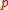 divides
dividesDivisibility (ring theory)
In mathematics, the notion of a divisor originally arose within the context of arithmetic of whole numbers. Please see the page about divisors for this simplest example. With the development of abstract rings, of which the integers are the archetype, the original notion of divisor found a natural...
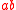 for some
for some  and
and 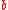 in
in  , then
, then 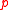 divides
divides  or
or 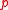 divides
divides  . Equivalently, an element
. Equivalently, an element 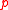 is prime if, and only if, the principal ideal
is prime if, and only if, the principal idealPrincipal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
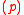 generated by
generated by 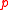 is a nonzero prime ideal
is a nonzero prime idealPrime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
.
Interest in prime elements comes from the Fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
, which asserts that each integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
can be written in essentially only one way as 1 or −1 multiplied by a product of positive prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. This led to the study of unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
s, which generalize what was just illustrated in the integers.
Prime elements should not be confused with irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
s. In an integral domain, every prime is irreducible but the converse is not true in general. However, in unique factorization domains, or more generally in GCD domain
GCD domain
In mathematics, a GCD domain is an integral domain R with the property that any two non-zero elements have a greatest common divisor . Equivalently, any two non-zero elements of R have a least common multiple ....
s, primes and irreducibles are the same.
Being prime is also relative to which ring an element is considered to be in; for example, 2 is a prime element in Z but it is not in Z[
 ], the ring of Gaussian integers, since
], the ring of Gaussian integers, since 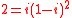 and 2 does not divide any factor on the right.
and 2 does not divide any factor on the right.Examples
The following are examples of prime elements in rings:- The integers ±2, ±3, ±5, ±7, ±11,... in the ring of integersRing of integersIn mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
Z - the complex numbers (
 ), 19, and (
), 19, and ( ) in the ring of Gaussian integers Z[
) in the ring of Gaussian integers Z[ ]
] - the polynomials
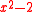 and
and  in the ring of polynomials over Z.
in the ring of polynomials over Z.

