Divisibility (ring theory)
Encyclopedia
In mathematics
, the notion of a divisor originally arose within the context of arithmetic of whole numbers. Please see the page about divisor
s for this simplest example. With the development of abstract rings
, of which the integers are the archetype, the original notion of divisor found a natural extension. Divisibility is a useful concept for the analysis of the structure of commutative rings because of its relationship with the ideal structure of such rings.
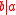) if there exists an element x in R with 
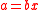. We also say that b is a divisor of a, or that a is a multiple
of b.
Notes: This definition makes sense when R is any commutative semigroup
, but virtually the only time divisors are discussed is when this semi-group is the multiplicative monoid
of a commutative ring with identity. Also, divisors are also occasionally useful in non-commutative contexts, where one must then discuss left and right divisors.
Elements a and b of a commutative ring are said to be associates if both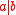
and 
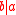. The associate relationship is an equivalence relation
on R, and hence divides R into disjoint equivalence classes each of which consists of all elements of R that are associates of any particular member of the class.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of a divisor originally arose within the context of arithmetic of whole numbers. Please see the page about divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s for this simplest example. With the development of abstract rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, of which the integers are the archetype, the original notion of divisor found a natural extension. Divisibility is a useful concept for the analysis of the structure of commutative rings because of its relationship with the ideal structure of such rings.
Definition
A nonzero element b of a commutative ring R is said to divide an element a in R (notation: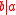) if there exists an element x in R with 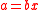. We also say that b is a divisor of a, or that a is a multipleMultiple
The word multiple can refer to:*Multiple , multiples of numbers*List of multiple discoveries, instances of scientists, working independently of each other, reaching similar findings...
of b.
Notes: This definition makes sense when R is any commutative semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
, but virtually the only time divisors are discussed is when this semi-group is the multiplicative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
of a commutative ring with identity. Also, divisors are also occasionally useful in non-commutative contexts, where one must then discuss left and right divisors.
Elements a and b of a commutative ring are said to be associates if both
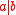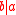and . The associate relationship is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on R, and hence divides R into disjoint equivalence classes each of which consists of all elements of R that are associates of any particular member of the class.
Properties
If R has an identity, then most statements about divisibility can be translated into statements about principal ideals. For instance,-
if and only if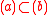 
. - a and b are associates if and only if
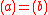
- u is a unit if and only if u is a divisor of every element of R
- u is a unit if and only if
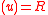. - If
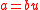where u is a unit, then a and b are associates. If R is an integral domain, then the converse is true.