
Semigroup
Encyclopedia
In mathematics, a semigroup is an algebraic structure
consisting of a set together with an associative binary operation
. A semigroup generalizes a monoid
in that there might not exist an identity element
. It also (originally) generalized a group
(a monoid with all inverses) to a type where every element did not have to have an inverse
, thus the name semigroup.
The binary operation of a semigroup is most often denoted multiplicatively: , or simply
, or simply  , denotes the result of applying the semigroup operation to the ordered pair
, denotes the result of applying the semigroup operation to the ordered pair 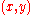 . The operation is required to be associative so that
. The operation is required to be associative so that 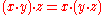 for all x, y and z, but need not be commutative
for all x, y and z, but need not be commutative
so that does not have to equal
does not have to equal  (contrast to the regular multiplication operator where ).
(contrast to the regular multiplication operator where ).
By definition, a semigroup is an associative magma
. A semigroup with an identity element is called a monoid
. A group
is then a monoid in which every element has an inverse element. Semigroups must not be confused with quasigroup
s which are sets with a not necessarily associative binary operation such that division is always possible.
The formal study of semigroups began in the early 20th century. Semigroups are important in many areas of mathematics because they are the abstract algebraic underpinning of "memoryless" systems: time-dependent systems that start from scratch at each iteration. In applied mathematics
, semigroups are fundamental models for linear time-invariant systems. In partial differential equations, a semigroup is associated to any equation whose spatial evolution is independent of time. The theory of finite semigroups has been of particular importance in theoretical computer science
since the 1950s because of the natural link between finite semigroups and finite automata. In probability theory
, semigroups are associated with Markov process
es .
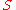 , together with a binary operation
, together with a binary operation
" " that satisfies:
" that satisfies:
Closure: For all a, b in S, the result of the operation a · b is also in S.
Associativity
: For all a, b and c in S, the equation (a · b) · c = a · (b · c) holds.
And in mathematical notation we have:
More compactly, a semigroup is an associative magma
.
, has at most one identity element
. A semigroup with identity is called a monoid
. A semigroup without identity may be embedded
into a monoid simply by adjoining an element to
to  and defining
and defining  for all
for all  . The notation S1 denotes a monoid obtained from S by adjoining an identity if necessary (S1 = S for a monoid). Thus, every commutative semigroup can be embedded in a group via the Grothendieck group
. The notation S1 denotes a monoid obtained from S by adjoining an identity if necessary (S1 = S for a monoid). Thus, every commutative semigroup can be embedded in a group via the Grothendieck group
construction.
Similary, every magma has at most one absorbing element
, which in semigroup theory is called a zero. Analogous to the above construction, for every semigroup S, one defines S0, a semigroup with 0 that embeds S.
If A is both a left ideal and a right ideal then it is called an ideal (or a two-sided ideal).
If S is a semigroup, then the intersection of any collection of subsemigroups of S is also a subsemigroup of S.
So the subsemigroups of S form a complete lattice
.
An example of semigroup with no minimal ideal is the set of positive integers under addition. The minimal ideal of a commutative semigroup, when it exists, is a group.
Green's relations
, a set of five equivalence relation
s that characterise the elements in terms of the principal ideal
s they generate, are important tools for analysing the ideals of a semigroup and related notions of structure.
is a function that preserves semigroup structure. A function f: S → T between two semigroups is a homomorphism if the equation
holds for all elements a, b in S, i.e. the result is the same when performing the semigroup operation after or before applying the map f.
A semigroup homomorphism between monoids preserves identity iff it is a monoid homomorphism. But there are semigroup homomorphisms which are not monoid homomorphisms, e.g. the canonical embedding of a semigroup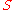 without identity into
without identity into  . Conditions characterizing monoid homomorphisms are discussed further. Let
. Conditions characterizing monoid homomorphisms are discussed further. Let  be a semigroup homomorphism. The image of
be a semigroup homomorphism. The image of  is also a semigroup. If
is also a semigroup. If  is a monoid with an identity element
is a monoid with an identity element  , then
, then 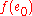 is the identity element in the image of
is the identity element in the image of  . If
. If 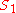 is also a monoid with an identity element
is also a monoid with an identity element  and
and  belongs to the image of
belongs to the image of  , then
, then 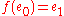 , i.e.
, i.e.  is a monoid homomorphism. Particularly, if
is a monoid homomorphism. Particularly, if  is surjective, then it is a monoid homomorphism.
is surjective, then it is a monoid homomorphism.
Two semigroups S and T are said to be isomorphic
if there is a bijection
f : S ↔ T with the property that, for any elements a, b in S, f(ab) = f(a)f(b). Isomorphic semigroups have the same structure.
A semigroup congruence is an equivalence relation
is an equivalence relation
that is compatible with the semigroup operation. That is, a subset that is an equivalence relation and
that is an equivalence relation and 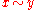 and
and  implies
implies  for every
for every  in S. Like any equivalence relation, a semigroup congruence
in S. Like any equivalence relation, a semigroup congruence  induces congruence classes
induces congruence classes
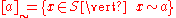
and the semigroup operation induces a binary operation on the congruence classes:
on the congruence classes:

Because is a congruence, the set of all congruence classes of
is a congruence, the set of all congruence classes of  forms a semigroup with
forms a semigroup with  , called the quotient semigroup or factor semigroup, and denoted
, called the quotient semigroup or factor semigroup, and denoted 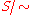 . The mapping
. The mapping  is a semigroup homomorphism, called the quotient map, canonical surjection or projection; if S is a monoid then quotient semigroup is a monoid with identity
is a semigroup homomorphism, called the quotient map, canonical surjection or projection; if S is a monoid then quotient semigroup is a monoid with identity  . Conversely, the kernel of any semigroup homomorphism is a semigroup congruence. These results are nothing more than a particularization of the first isomorphism theorem in universal algebra. Congruence classes and factor monoids are the objects of study in string rewriting systems.
. Conversely, the kernel of any semigroup homomorphism is a semigroup congruence. These results are nothing more than a particularization of the first isomorphism theorem in universal algebra. Congruence classes and factor monoids are the objects of study in string rewriting systems.
Every ideal I of a semigroup induces a subsemigroup, the Rees factor semigroup
via the congruence x ρ y ⇔ either x = y or both x and y are in I.
If this is finite, then x is said to be of finite order, otherwise it is of infinite order.
A semigroup is said to be periodic if all of its elements are of finite order.
A semigroup generated by a single element is said to be monogenic
(or cyclic). If a monogenic semigroup is infinite then it is isomorphic to the semigroup of positive integer
s with the operation of addition.
If it is finite and nonempty, then it must contain at least one idempotent.
It follows that every nonempty periodic semigroup has at least one idempotent.
A subsemigroup which is also a group is called a subgroup
. There is a close relationship between the subgroups of a semigroup and its idempotents. Each subgroup contains exactly one idempotent, namely the identity element of the subgroup. For each idempotent e of the semigroup there is a unique maximal subgroup containing e. Each maximal subgroup arises in this way, so there is a one-to-one correspondence between idempotents and maximal subgroups. Here the term maximal subgroup
differs from its standard use in group theory.
More can often be said when the order is finite. For example, every nonempty finite semigroup is periodic, and has a minimal ideal
and at least one idempotent. For more on the structure of finite semigroups, see Krohn-Rhodes theory
.
An important question is to characterize those semigroups for which this map is an embedding. This need not always be the case: for example, take S to be the semigroup of subsets of some set X with set-theoretic intersection as the binary operation (this is an example of a semilattice). Since A.A = A holds for all elements of S, this must be true for all generators of G(S) as well: which is therefore the trivial group
. It is clearly necessary for embeddability that S have the cancellation property
. When S is commutative this condition is also sufficient and the Grothendieck group
of the semigroup provides a construction of the group of fractions. The problem for non-commutative semigroups can be traced to the first substantial paper on semigroups, . Anatoly Maltsev
gave necessary and conditions for embeddability in 1937.
on a function space. For example, consider the following initial/boundary value problem for the heat equation
on the spatial interval
(0, 1) ⊂ R and times t ≥ 0:
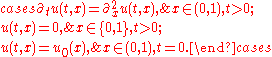
Let X be the Lp space
L2((0, 1); R) and let A be the second-derivative operator with domain
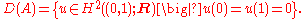
Then the above initial/boundary value problem can be interpreted as an initial value problem for an ordinary differential equation on the space X:

On an heuristic level, the solution to this problem "ought" to be u(t) = exp(tA)u0. However, for a rigorous treatment, a meaning must be given to the exponential
of tA. As a function of t, exp(tA) is a semigroup of operators from X to itself, taking the initial state u0 at time t = 0 to the state u(t) = exp(tA)u0 at time t. The operator A is said to be the infinitesimal generator of the semigroup.
or rings. A number of sources attribute the first use of the term (in French) to J.-A. de Séguier in Élements de la Théorie des Groupes Abstraits (Elements of the Theory of Abstract Groups) in 1904. The term is used in English in 1908 in Harold Hinton's Theory of Groups of Finite Order.
Anton Suschkewitsch obtained the first non-trivial results about semigroups. His 1928 paper Über die endlichen Gruppen ohne das Gesetz der eindeutigen Umkehrbarkeit (On finite groups without the rule of unique invertibility) determined the structure of finite simple semigroups and showed that the minimal ideal (or Green's relations
J-class) of a finite semigroup is simple. From that point on, the foundations of semigroup theory were further laid by David Rees
, James Alexander Green
, Evgenii Sergeevich Lyapin, Alfred H. Clifford
and Gordon Preston
. The latter two published a two-volume monograph on semigroup theory in 1961 and 1967 respectively. In 1970, a new periodical called Semigroup Forum
(currently edited by Springer Verlag) became one of the few mathematical journals devoted entirely to semigroup theory.
In recent years researchers in the field have became more specialized with dedicated monographs appearing on important classes of semigroups, like inverse semigroup
s, as well as monographs focusing on applications in algebraic automata theory, particularly for finite automata, and also in functional analysis
.
M × M → M.
Generalizing in a different direction, an n-ary semigroup (also n-semigroup, polyadic semigroup or multiary semigroup) is a generalization of a semigroup to a set G with a n-ary operation
instead of a binary operation. The associative law is generalized as follows: ternary associativity is , i.e. the string abcde with any three adjacent elements bracketed. N-ary associativity is a string of length with any n adjacent elements bracketed. A 2-ary semigroup is just a semigroup. Further axioms lead to an n-ary group
.
A third generalization is the semigroupoid
, in which the requirement that the binary relation be total is lifted. As categories generalize monoids in the same way, a semigroupoid behaves much like a category but lacks identities.
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
consisting of a set together with an associative binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
. A semigroup generalizes a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
in that there might not exist an identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. It also (originally) generalized a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(a monoid with all inverses) to a type where every element did not have to have an inverse
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
, thus the name semigroup.
The binary operation of a semigroup is most often denoted multiplicatively:
 , or simply
, or simply  , denotes the result of applying the semigroup operation to the ordered pair
, denotes the result of applying the semigroup operation to the ordered pair 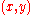 . The operation is required to be associative so that
. The operation is required to be associative so that 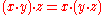 for all x, y and z, but need not be commutative
for all x, y and z, but need not be commutativeCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
so that
 does not have to equal
does not have to equal  (contrast to the regular multiplication operator where ).
(contrast to the regular multiplication operator where ).By definition, a semigroup is an associative magma
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
. A semigroup with an identity element is called a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. A group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is then a monoid in which every element has an inverse element. Semigroups must not be confused with quasigroup
Quasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
s which are sets with a not necessarily associative binary operation such that division is always possible.
The formal study of semigroups began in the early 20th century. Semigroups are important in many areas of mathematics because they are the abstract algebraic underpinning of "memoryless" systems: time-dependent systems that start from scratch at each iteration. In applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, semigroups are fundamental models for linear time-invariant systems. In partial differential equations, a semigroup is associated to any equation whose spatial evolution is independent of time. The theory of finite semigroups has been of particular importance in theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
since the 1950s because of the natural link between finite semigroups and finite automata. In probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, semigroups are associated with Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
es .
Definition
A semigroup is a set,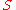 , together with a binary operation
, together with a binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
"
 " that satisfies:
" that satisfies:Closure: For all a, b in S, the result of the operation a · b is also in S.
Associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
: For all a, b and c in S, the equation (a · b) · c = a · (b · c) holds.
And in mathematical notation we have:
-
 and
and -
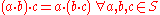 .
.
More compactly, a semigroup is an associative magma
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
.
Examples of semigroups
- Empty semigroupEmpty semigroupIn mathematics, a semigroup with no elements is a semigroup in which the underlying set is the empty set. Many authors do not admit the existence of such a semigroup. For them a semigroup is by definition a non-empty set together with an associative binary operation. However not all authors insist...
: the empty set forms a semigroup with the empty function as the binary operation. - Semigroup with one element: there is essentially just one, the singleton {a} with operation a · a = a.
- Semigroup with two elementsSemigroup with two elementsIn mathematics, a semigroup with two elements is a semigroup for which the cardinality of the underlying set is two. There are exactly five distinct nonisomorphic semigroups having two elements:* O2, the null semigroup of order two,...
: there are five which are essentially different. - The set of positive integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s with addition. - Square nonnegative matricesNonnegative matrixA nonnegative matrix is a matrix in which all the elements are equal to or greater than zeroA positive matrix is a matrix in which all the elements are greater than zero...
with matrix multiplication. - Any ideal of a ring with the multiplication of the ring.
- The set of all finite stringsString (computer science)In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
over a fixed alphabet Σ with concatenation of strings as the semigroup operation — the so-called "free semigroupFree semigroupIn abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
over Σ". With the empty string included, this semigroup becomes the free monoid over Σ. - A probability distribution F together with all convolution powers of F, with convolution as operation. This is called a convolution semigroup.
- A monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
is a semigroup with an identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. - A groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is a monoid in which every element has an inverse elementInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
. - Transformation semigroupTransformation semigroupIn algebra and theoretical computer science, an action or act of a semigroup on a set is a rule which associates to each element of the semigroup a transformation of the set in such a way that the product of two elements of the semigroup is associated with the composite of the two corresponding...
s and monoids
Identity and zero
Every semigroup, in fact every magmaMagma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
, has at most one identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. A semigroup with identity is called a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. A semigroup without identity may be embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
into a monoid simply by adjoining an element
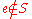 to
to  and defining
and defining  for all
for all  . The notation S1 denotes a monoid obtained from S by adjoining an identity if necessary (S1 = S for a monoid). Thus, every commutative semigroup can be embedded in a group via the Grothendieck group
. The notation S1 denotes a monoid obtained from S by adjoining an identity if necessary (S1 = S for a monoid). Thus, every commutative semigroup can be embedded in a group via the Grothendieck groupGrothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
construction.
Similary, every magma has at most one absorbing element
Absorbing element
In mathematics, an absorbing element is a special type of element of a set with respect to a binary operation on that set. The result of combining an absorbing element with any element of the set is the absorbing element itself. In semigroup theory, the absorbing element is called a zero element...
, which in semigroup theory is called a zero. Analogous to the above construction, for every semigroup S, one defines S0, a semigroup with 0 that embeds S.
Subsemigroups and ideals
The semigroup operation induces an operation on the collection of its subsets: given subsets A and B of a semigroup, A*B, written commonly as AB, is the set { ab | a in A and b in B }. In terms of this operations, a subset A is called- a subsemigroup if AA is a subset of A,
- a right ideal if AS is a subset of A, and
- a left ideal if SA is a subset of A.
If A is both a left ideal and a right ideal then it is called an ideal (or a two-sided ideal).
If S is a semigroup, then the intersection of any collection of subsemigroups of S is also a subsemigroup of S.
So the subsemigroups of S form a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
.
An example of semigroup with no minimal ideal is the set of positive integers under addition. The minimal ideal of a commutative semigroup, when it exists, is a group.
Green's relations
Green's relations
In mathematics, Green's relations are five equivalence relations that characterise the elements of a semigroup in terms of the principal ideals they generate. The relations are named for James Alexander Green, who introduced them in a paper of 1951...
, a set of five equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s that characterise the elements in terms of the principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
s they generate, are important tools for analysing the ideals of a semigroup and related notions of structure.
Homomorphisms and congruences
A semigroup homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
is a function that preserves semigroup structure. A function f: S → T between two semigroups is a homomorphism if the equation
- f(ab) = f(a)f(b).
holds for all elements a, b in S, i.e. the result is the same when performing the semigroup operation after or before applying the map f.
A semigroup homomorphism between monoids preserves identity iff it is a monoid homomorphism. But there are semigroup homomorphisms which are not monoid homomorphisms, e.g. the canonical embedding of a semigroup
 without identity into
without identity into  . Conditions characterizing monoid homomorphisms are discussed further. Let
. Conditions characterizing monoid homomorphisms are discussed further. Let  be a semigroup homomorphism. The image of
be a semigroup homomorphism. The image of  is also a semigroup. If
is also a semigroup. If  is a monoid with an identity element
is a monoid with an identity element  , then
, then 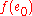 is the identity element in the image of
is the identity element in the image of  . If
. If 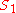 is also a monoid with an identity element
is also a monoid with an identity element  and
and  belongs to the image of
belongs to the image of  , then
, then 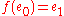 , i.e.
, i.e.  is a monoid homomorphism. Particularly, if
is a monoid homomorphism. Particularly, if  is surjective, then it is a monoid homomorphism.
is surjective, then it is a monoid homomorphism.Two semigroups S and T are said to be isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
if there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
f : S ↔ T with the property that, for any elements a, b in S, f(ab) = f(a)f(b). Isomorphic semigroups have the same structure.
A semigroup congruence
 is an equivalence relation
is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
that is compatible with the semigroup operation. That is, a subset
 that is an equivalence relation and
that is an equivalence relation and 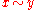 and
and  implies
implies  for every
for every  in S. Like any equivalence relation, a semigroup congruence
in S. Like any equivalence relation, a semigroup congruence  induces congruence classes
induces congruence classes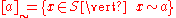
and the semigroup operation induces a binary operation
 on the congruence classes:
on the congruence classes:
Because
 is a congruence, the set of all congruence classes of
is a congruence, the set of all congruence classes of  forms a semigroup with
forms a semigroup with  , called the quotient semigroup or factor semigroup, and denoted
, called the quotient semigroup or factor semigroup, and denoted 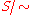 . The mapping
. The mapping  is a semigroup homomorphism, called the quotient map, canonical surjection or projection; if S is a monoid then quotient semigroup is a monoid with identity
is a semigroup homomorphism, called the quotient map, canonical surjection or projection; if S is a monoid then quotient semigroup is a monoid with identity  . Conversely, the kernel of any semigroup homomorphism is a semigroup congruence. These results are nothing more than a particularization of the first isomorphism theorem in universal algebra. Congruence classes and factor monoids are the objects of study in string rewriting systems.
. Conversely, the kernel of any semigroup homomorphism is a semigroup congruence. These results are nothing more than a particularization of the first isomorphism theorem in universal algebra. Congruence classes and factor monoids are the objects of study in string rewriting systems.Every ideal I of a semigroup induces a subsemigroup, the Rees factor semigroup
Rees factor semigroup
In mathematics, in semigroup theory, a Rees factor semigroup is a certain semigroup constructed using a semigroup and an ideal of the semigroup....
via the congruence x ρ y ⇔ either x = y or both x and y are in I.
Structure of semigroups
For any subset A of S there is a smallest subsemigroup T of S which contains A, and we say that A generates T. A single element x of S generates the subsemigroup { xn | n is a positive integer }.If this is finite, then x is said to be of finite order, otherwise it is of infinite order.
A semigroup is said to be periodic if all of its elements are of finite order.
A semigroup generated by a single element is said to be monogenic
Monogenic semigroup
In mathematics, a monogenic semigroup is a semigroup generated by a set containing only a single element. Monogenic semigroups are also called cyclic semigroups.-Structure:...
(or cyclic). If a monogenic semigroup is infinite then it is isomorphic to the semigroup of positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s with the operation of addition.
If it is finite and nonempty, then it must contain at least one idempotent.
It follows that every nonempty periodic semigroup has at least one idempotent.
A subsemigroup which is also a group is called a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
. There is a close relationship between the subgroups of a semigroup and its idempotents. Each subgroup contains exactly one idempotent, namely the identity element of the subgroup. For each idempotent e of the semigroup there is a unique maximal subgroup containing e. Each maximal subgroup arises in this way, so there is a one-to-one correspondence between idempotents and maximal subgroups. Here the term maximal subgroup
Maximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
differs from its standard use in group theory.
More can often be said when the order is finite. For example, every nonempty finite semigroup is periodic, and has a minimal ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
and at least one idempotent. For more on the structure of finite semigroups, see Krohn-Rhodes theory
Krohn-Rhodes theory
In mathematics and computer science, the Krohn–Rhodes theory is an approach to the study of finite semigroups and automata that seeks to decompose them in terms of elementary components...
.
Special classes of semigroups
- A monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
is a semigroup with identity. - A subsemigroup is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a semigroup that is closed under the semigroup operation. - A bandBand (algebra)In mathematics, a band is a semigroup in which every element is idempotent . Bands were first studied and named by ; the lattice of varieties of bands was described independently in the early 1970s by Biryukov, Fennemore and Gerhard...
is a semigroup the operation of which is idempotent. - A cancellative semigroupCancellative semigroupIn mathematics, a cancellative semigroup is a semigroup having the cancellation property. In intuitive terms, the cancellation property asserts that from an equality of the form a · b = a · c, where · is a binary operation, one can cancel the element a and deduce the equality b = c...
is one having the cancellation propertyCancellation propertyIn mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
: a · b = a · c implies b = c and similarly for b · a = c · a. - SemilatticeSemilatticeIn mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
s: A semigroup whose operation is idempotent and commutativeCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
is a semilatticeSemilatticeIn mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
. - 0-simple semigroups.
- Transformation semigroupTransformation semigroupIn algebra and theoretical computer science, an action or act of a semigroup on a set is a rule which associates to each element of the semigroup a transformation of the set in such a way that the product of two elements of the semigroup is associated with the composite of the two corresponding...
s: any finite semigroup S can be represented by transformations of a (state-) set Q of at most |S|+1 states. Each element x of S then maps Q into itself x: Q → Q and sequence xy is defined by q(xy) = (qx)y for each q in Q. Sequencing clearly is an associative operation, here equivalent to function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. This representation is basic for any automatonAutomatonAn automaton is a self-operating machine. The word is sometimes used to describe a robot, more specifically an autonomous robot. An alternative spelling, now obsolete, is automation.-Etymology:...
or finite state machineFinite state machineA finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
(FSM). - The bicyclic semigroupBicyclic semigroupIn mathematics, the bicyclic semigroup is an algebraic object important for the structure theory of semigroups. Although it is in fact a monoid, it is usually referred to as simply a semigroup. The first published description of this object was given by Evgenii Lyapin in 1953. Alfred H...
is in fact a monoid, which can be described as the free semigroupFree semigroupIn abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
on two generators p and q, under the relation p q = 1. - C0-semigroupsC0-semigroupIn mathematics, a C0-semigroup, also known as a strongly continuous one-parameter semigroup, is a generalization of the exponential function...
. - Regular semigroupRegular semigroupA regular semigroup is a semigroup S in which every element is regular, i.e., for each element a, there exists an element x such that axa = a. Regular semigroups are one of the most-studied classes of semigroups, and their structure is particularly amenable to study via Green's relations.- Origins...
s. Every element x has at least one inverse y satisfying xyx=x and yxy=y; the elements x and y are sometimes called "mutually inverse". - Inverse semigroupInverse semigroupIn mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
s are regular semigroups where every element has exactly one inverse. Alternatively, a regular semigroup is inverse if and only if any two idempotents commute. - Affine semigroup: a semigroup that is isomorphic to a finitely-generated subsemigroup of Zd. These semigroups have applications to commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
.
Group of fractions
The group of fractions of a semigroup S is the group G = G(S) generated by the elements of S as generators and all equations xy=z which hold true in S as relations. This has a universal property for morphisms from S to a group. There is an obvious map from S to G(S) by sending each element of S to the corresponding generator.An important question is to characterize those semigroups for which this map is an embedding. This need not always be the case: for example, take S to be the semigroup of subsets of some set X with set-theoretic intersection as the binary operation (this is an example of a semilattice). Since A.A = A holds for all elements of S, this must be true for all generators of G(S) as well: which is therefore the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
. It is clearly necessary for embeddability that S have the cancellation property
Cancellation property
In mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
. When S is commutative this condition is also sufficient and the Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
of the semigroup provides a construction of the group of fractions. The problem for non-commutative semigroups can be traced to the first substantial paper on semigroups, . Anatoly Maltsev
Anatoly Maltsev
Anatoly Ivanovich Maltsev was born in Misheronsky, near Moscow, and died in Novosibirsk, USSR. He was a mathematician noted for his work on the decidability of various algebraic groups...
gave necessary and conditions for embeddability in 1937.
Semigroup methods in partial differential equations
Semigroup theory can be used to study some problems in the field of partial differential equations. Roughly speaking, the semigroup approach is to regard a time-dependent partial differential equation as an ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
on a function space. For example, consider the following initial/boundary value problem for the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
on the spatial interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(0, 1) ⊂ R and times t ≥ 0:
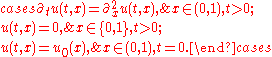
Let X be the Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
L2((0, 1); R) and let A be the second-derivative operator with domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
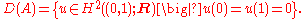
Then the above initial/boundary value problem can be interpreted as an initial value problem for an ordinary differential equation on the space X:

On an heuristic level, the solution to this problem "ought" to be u(t) = exp(tA)u0. However, for a rigorous treatment, a meaning must be given to the exponential
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of tA. As a function of t, exp(tA) is a semigroup of operators from X to itself, taking the initial state u0 at time t = 0 to the state u(t) = exp(tA)u0 at time t. The operator A is said to be the infinitesimal generator of the semigroup.
History
The study of semigroups trailed behind that of other algebraic structures with more complex axioms such as groupsGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
or rings. A number of sources attribute the first use of the term (in French) to J.-A. de Séguier in Élements de la Théorie des Groupes Abstraits (Elements of the Theory of Abstract Groups) in 1904. The term is used in English in 1908 in Harold Hinton's Theory of Groups of Finite Order.
Anton Suschkewitsch obtained the first non-trivial results about semigroups. His 1928 paper Über die endlichen Gruppen ohne das Gesetz der eindeutigen Umkehrbarkeit (On finite groups without the rule of unique invertibility) determined the structure of finite simple semigroups and showed that the minimal ideal (or Green's relations
Green's relations
In mathematics, Green's relations are five equivalence relations that characterise the elements of a semigroup in terms of the principal ideals they generate. The relations are named for James Alexander Green, who introduced them in a paper of 1951...
J-class) of a finite semigroup is simple. From that point on, the foundations of semigroup theory were further laid by David Rees
David Rees (mathematician)
David Rees ScD Cantab, FIMA, FRS is an emeritus professor of pure mathematics at the University of Exeter, having been head of the Mathematics / Mathematical Sciences Department at Exeter for many years....
, James Alexander Green
James Alexander Green
James Alexander "Sandy" Green FRS is a mathematician and retired Professor at the Mathematics Institute at the University of Warwick, who is still active in the field of representation theory.-Early life:...
, Evgenii Sergeevich Lyapin, Alfred H. Clifford
Alfred H. Clifford
Alfred Hoblitzelle Clifford was an American mathematician who is known for Clifford theory and for his work on semigroups. The Alfred H. CliffordMathematics Research Library at Tulane University is named after him....
and Gordon Preston
Gordon Preston
Gordon Bamford Preston is an English mathematician who is known for his work on semigroups. He received his D.Phil. in mathematics in 1954 from the University of Oxford.He was born in Workington and brought up in Carlisle...
. The latter two published a two-volume monograph on semigroup theory in 1961 and 1967 respectively. In 1970, a new periodical called Semigroup Forum
Semigroup Forum
Semigroup Forum is a mathematics research journal published by Springer. The journal serves as a platform for the speedy and efficient transmission of information on current research in semigroup theory...
(currently edited by Springer Verlag) became one of the few mathematical journals devoted entirely to semigroup theory.
In recent years researchers in the field have became more specialized with dedicated monographs appearing on important classes of semigroups, like inverse semigroup
Inverse semigroup
In mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
s, as well as monographs focusing on applications in algebraic automata theory, particularly for finite automata, and also in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
Generalizations
If the associativity axiom of a semigroup is dropped, the result is a magma, which is nothing more than a set M equipped with a binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
M × M → M.
Generalizing in a different direction, an n-ary semigroup (also n-semigroup, polyadic semigroup or multiary semigroup) is a generalization of a semigroup to a set G with a n-ary operation
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
instead of a binary operation. The associative law is generalized as follows: ternary associativity is , i.e. the string abcde with any three adjacent elements bracketed. N-ary associativity is a string of length with any n adjacent elements bracketed. A 2-ary semigroup is just a semigroup. Further axioms lead to an n-ary group
N-ary group
In mathematics, an n-ary group is a generalization of a group to a set G with a n-ary operation instead of a binary operation. The axioms for an n-ary group are defined in such a way as to reduce to those of a group in the case .-Associativity:The easiest axiom to generalize is the associative law...
.
A third generalization is the semigroupoid
Semigroupoid
In mathematics, a semigroupoid is a partial algebra which satisfies the axioms for a small category, except possibly for the requirement that there be an identity at each object...
, in which the requirement that the binary relation be total is lifted. As categories generalize monoids in the same way, a semigroupoid behaves much like a category but lacks identities.
See also
- Absorbing elementAbsorbing elementIn mathematics, an absorbing element is a special type of element of a set with respect to a binary operation on that set. The result of combining an absorbing element with any element of the set is the absorbing element itself. In semigroup theory, the absorbing element is called a zero element...
- Biordered setBiordered setA biordered set is a mathematical object that occurs in the description of the structure of the set of idempotents in a semigroup. The concept and the terminology were developed by K S S Nambooripad of Kerala, India, in the early 1970s....
- Empty semigroupEmpty semigroupIn mathematics, a semigroup with no elements is a semigroup in which the underlying set is the empty set. Many authors do not admit the existence of such a semigroup. For them a semigroup is by definition a non-empty set together with an associative binary operation. However not all authors insist...
- Identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
- Light's associativity testLight's associativity testIn mathematics, Light's associativity test is a procedure invented by F W Light for testing whether a binary operation defined in a finite set by a Cayley multiplication table is associative. Direct verification of the associativity of a binary operation specified by a Cayley table is cumbersome...
- Weak inverseWeak inverse- Theory of semigroups :In the theory of semigroups, a weak inverse of an element x in a semigroup is an element y such that .An element x of S for which there is an element y of S such that is called regular...

