Bicyclic semigroup
Encyclopedia
In mathematics
, the bicyclic semigroup is an algebraic object important for the structure theory of semigroup
s. Although it is in fact a monoid
, it is usually referred to as simply a semigroup. The first published description of this object was given by Evgenii Lyapin in 1953. Alfred H. Clifford
and Gordon Preston
claim that one of them, working with David Rees
, discovered it independently (without publication) at some point before 1943.
; and most recent papers have tended to use B. This article will use the modern style throughout.
on two generators p and q, under the relation p q = 1. That is, each semigroup element is a string of those two letters, with the proviso that the subsequence "p q" does not appear. The semigroup operation is concatenation of strings, which is clearly associative. It can then be shown that all elements of B in fact have the form qa pb, for some natural number
s a and b. The composition operation simplifies to
This is sufficient to define B so that it is the same object as in the original construction. Just as p and q generated B originally, with the empty string as the monoid identity, this new construction of B has generators (1, 0) and (0, 1), with identity (0, 0).
to the bicyclic semigroup.
It is not entirely obvious that this should be the case—perhaps the hardest task is understanding that S must be infinite. To see this, suppose that a (say) does not have infinite order, so ak + h = ah for some h and k. Then ak = e, and
so
which is not allowed—so there are infinitely many distinct powers of a. The full proof is given in Clifford and Preston's book.
Note that the two definitions given above both satisfy these properties. A third way of deriving B uses two appropriately-chosen functions to yield the bicyclic semigroup as a monoid of transformations of the natural numbers. Let α, β, and ι be elements of the transformation semigroup
on the natural numbers, where
These three functions have the required properties, so the semigroup they generate is B.
φ from B to another semigroup S is either cyclic, or it is an isomorphic copy of B. The elements φ(a), φ(b) and φ(e) of S will always satisfy the conditions above (because φ is a morphism) with the possible exception that φ(b) φ(a) might turn out to be φ(e). If this is not true, then φ(B) is isomorphic to B; otherwise, it is the cyclic semigroup generated by φ(a). In practice, this means that the bicyclic semigroup can be found in many different contexts.
The idempotents of B are all pairs (x, x), where x is any natural number (using the ordered pair characterisation of B). Since these commute, and B is regular (for every x there is a y such that x y x = x), the bicyclic semigroup is an inverse semigroup
. (This means that each element x of B has a unique inverse y, in the "weak" semigroup sense that x y x = x and y x y = y.)
Every ideal
of B is principal: the left and right principal ideals of (m, n) are
Each of these contains infinitely many others, so B does not have minimal left or right ideals.
In terms of Green's relations
, B has only one D-class (it is bisimple), and hence has only one J-class (it is simple). The L and R relations are given by
This implies that two elements are H-related if and only if they are identical. Consequently, the only subgroups of B are infinitely many copies of the trivial group, each corresponding to one of the idempotents.
The egg-box diagram
for B is infinitely large; the upper left corner begins:
Each entry represents a singleton H-class; the rows are the R-classes and the columns are L-classes. The idempotents of B appear down the diagonal, in accordance with the fact that in a regular semigroup with commuting idempotents, each L-class and each R-class must contain exactly one idempotent.
The bicyclic semigroup is the "simplest" example of a bisimple inverse semigroup with identity; there are many others. Where the definition of B from ordered pairs used the class of natural numbers (which is not only an additive semigroup, but also a commutative lattice
under min and max operations), another set with appropriate properties could appear instead, and the "+", "−" and "max" operations modified accordingly.
, as the syntactic monoid
of the Dyck language
. The Dyck language is the set of all strings of balanced pairs of parentheses, and thus finds common applications in defining binary tree
s and associative algebra
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the bicyclic semigroup is an algebraic object important for the structure theory of semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s. Although it is in fact a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
, it is usually referred to as simply a semigroup. The first published description of this object was given by Evgenii Lyapin in 1953. Alfred H. Clifford
Alfred H. Clifford
Alfred Hoblitzelle Clifford was an American mathematician who is known for Clifford theory and for his work on semigroups. The Alfred H. CliffordMathematics Research Library at Tulane University is named after him....
and Gordon Preston
Gordon Preston
Gordon Bamford Preston is an English mathematician who is known for his work on semigroups. He received his D.Phil. in mathematics in 1954 from the University of Oxford.He was born in Workington and brought up in Carlisle...
claim that one of them, working with David Rees
David Rees (mathematician)
David Rees ScD Cantab, FIMA, FRS is an emeritus professor of pure mathematics at the University of Exeter, having been head of the Mathematics / Mathematical Sciences Department at Exeter for many years....
, discovered it independently (without publication) at some point before 1943.
Construction
There are at least three standard ways of constructing the bicyclic semigroup, and various notations for referring to it. Lyapin called it P; Clifford and Preston used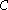; and most recent papers have tended to use B. This article will use the modern style throughout.From a free semigroup
The bicyclic semigroup is the free semigroupFree semigroup
In abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
on two generators p and q, under the relation p q = 1. That is, each semigroup element is a string of those two letters, with the proviso that the subsequence "p q" does not appear. The semigroup operation is concatenation of strings, which is clearly associative. It can then be shown that all elements of B in fact have the form qa pb, for some natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s a and b. The composition operation simplifies to
- (qa pb) (qc pd) = qa − b + max{b, c} pd − c + max{b, c}.
From ordered pairs
The way in which these exponents are constrained suggests that the "p and q structure" can be discarded, leaving only operations on the "a and b" part. So B is the semigroup of pairs of natural numbers (including zero), with operation (c, d) = (a − b + max{b, c}, d − c + max{b, c}).This is sufficient to define B so that it is the same object as in the original construction. Just as p and q generated B originally, with the empty string as the monoid identity, this new construction of B has generators (1, 0) and (0, 1), with identity (0, 0).
From functions
It can be shown that any semigroup S generated by elements e, a, and b satisfying the statements below is isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the bicyclic semigroup.
- a e = e a = a
- b e = e b = b
- a b = e
- b a ≠ e
It is not entirely obvious that this should be the case—perhaps the hardest task is understanding that S must be infinite. To see this, suppose that a (say) does not have infinite order, so ak + h = ah for some h and k. Then ak = e, and
- b = e b = ak b = ak - 1 e = ak - 1,
so
- b a = ak = e,
which is not allowed—so there are infinitely many distinct powers of a. The full proof is given in Clifford and Preston's book.
Note that the two definitions given above both satisfy these properties. A third way of deriving B uses two appropriately-chosen functions to yield the bicyclic semigroup as a monoid of transformations of the natural numbers. Let α, β, and ι be elements of the transformation semigroup
Transformation semigroup
In algebra and theoretical computer science, an action or act of a semigroup on a set is a rule which associates to each element of the semigroup a transformation of the set in such a way that the product of two elements of the semigroup is associated with the composite of the two corresponding...
on the natural numbers, where
- ι(n) = n
- α(n) = n + 1
- β(n) = 0 if n = 0, and n − 1 otherwise.
These three functions have the required properties, so the semigroup they generate is B.
Properties
The bicyclic semigroup has the property that the image of any morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
φ from B to another semigroup S is either cyclic, or it is an isomorphic copy of B. The elements φ(a), φ(b) and φ(e) of S will always satisfy the conditions above (because φ is a morphism) with the possible exception that φ(b) φ(a) might turn out to be φ(e). If this is not true, then φ(B) is isomorphic to B; otherwise, it is the cyclic semigroup generated by φ(a). In practice, this means that the bicyclic semigroup can be found in many different contexts.
The idempotents of B are all pairs (x, x), where x is any natural number (using the ordered pair characterisation of B). Since these commute, and B is regular (for every x there is a y such that x y x = x), the bicyclic semigroup is an inverse semigroup
Inverse semigroup
In mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
. (This means that each element x of B has a unique inverse y, in the "weak" semigroup sense that x y x = x and y x y = y.)
Every ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of B is principal: the left and right principal ideals of (m, n) are
- (m, n) B = {(s, t) : s ≥ m} and
- B (m, n) = {(s, t) : t ≥ n}.
Each of these contains infinitely many others, so B does not have minimal left or right ideals.
In terms of Green's relations
Green's relations
In mathematics, Green's relations are five equivalence relations that characterise the elements of a semigroup in terms of the principal ideals they generate. The relations are named for James Alexander Green, who introduced them in a paper of 1951...
, B has only one D-class (it is bisimple), and hence has only one J-class (it is simple). The L and R relations are given by
- (a, b) R (c, d) if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
a = c; and - (a, b) L (c, d) if and only if b = d.
This implies that two elements are H-related if and only if they are identical. Consequently, the only subgroups of B are infinitely many copies of the trivial group, each corresponding to one of the idempotents.
The egg-box diagram
Green's relations
In mathematics, Green's relations are five equivalence relations that characterise the elements of a semigroup in terms of the principal ideals they generate. The relations are named for James Alexander Green, who introduced them in a paper of 1951...
for B is infinitely large; the upper left corner begins:
| (0, 0) | (1, 0) | (2, 0) | ... |
| (0, 1) | (1, 1) | (2, 1) | ... |
| (0, 2) | (1, 2) | (2, 2) | ... |
| ... | ... | ... | ... |
Each entry represents a singleton H-class; the rows are the R-classes and the columns are L-classes. The idempotents of B appear down the diagonal, in accordance with the fact that in a regular semigroup with commuting idempotents, each L-class and each R-class must contain exactly one idempotent.
The bicyclic semigroup is the "simplest" example of a bisimple inverse semigroup with identity; there are many others. Where the definition of B from ordered pairs used the class of natural numbers (which is not only an additive semigroup, but also a commutative lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
under min and max operations), another set with appropriate properties could appear instead, and the "+", "−" and "max" operations modified accordingly.
Relation to combinatorics
The bicyclic monoid occurs in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, as the syntactic monoid
Syntactic monoid
In mathematics and computer science, the syntactic monoid M of a formal language L is the smallest monoid that recognizes the language L.-Syntactic quotient:...
of the Dyck language
Dyck language
In the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of parentheses [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of parentheses, such as arithmetic...
. The Dyck language is the set of all strings of balanced pairs of parentheses, and thus finds common applications in defining binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
s and associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s.