Absorbing element
Encyclopedia
In mathematics
, an absorbing element is a special type of element of a set with respect to a binary operation
on that set. The result of combining an absorbing element with any element of the set is the absorbing element itself. In semigroup
theory, the absorbing element is called a zero element because there is no risk of confusion with other notions
of zero. In this article the two notions are synonymous.
). A zero element is an element z such that for all s in S, z∘s=s∘z=z. A refinement are the notions of left zero, where one requires only that z∘s=z, and right zero, where s∘z=z.
Absorbing elements are particularly interesting for semigroup
s, especially the multiplicative semigroup of a semiring
. In the case of a semiring with 0, the definition of an absorbing element is sometimes relaxed so that it is not required to absorb 0; otherwise, 0 would be the only absorbing element.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an absorbing element is a special type of element of a set with respect to a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
on that set. The result of combining an absorbing element with any element of the set is the absorbing element itself. In semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
theory, the absorbing element is called a zero element because there is no risk of confusion with other notions
Zero element
In mathematics, a zero element is one of several generalizations of the number zero to other algebraic structures. These alternate meanings may or may not reduce to the same thing, depending on the context.-Additive identities:...
of zero. In this article the two notions are synonymous.
Definition
Formally, let (S, ∘) be a set S with a binary operation ∘ on it (known as a magmaMagma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
). A zero element is an element z such that for all s in S, z∘s=s∘z=z. A refinement are the notions of left zero, where one requires only that z∘s=z, and right zero, where s∘z=z.
Absorbing elements are particularly interesting for semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s, especially the multiplicative semigroup of a semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
. In the case of a semiring with 0, the definition of an absorbing element is sometimes relaxed so that it is not required to absorb 0; otherwise, 0 would be the only absorbing element.
Properties
- If a magma has both a left zero
and a right zero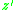 
, then it has a zero, since 
. - If a magma has a zero element, then the zero element is uniqueUniqueness quantificationIn mathematics and logic, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic, this sort of quantification is known as uniqueness quantification or unique existential quantification.Uniqueness quantification is...
.
Examples
- The set of binary relations over a set X, together with the composition of relationsComposition of relationsIn mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
forms a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
with zero, where the zero element is the empty relation (empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
). - The closed interval H=
[ 0, 1] with x∘y=min(x,y) is also a monoid with zero, and the zero element is 0. - More examples:
set operation absorber real number Real numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s· (multiplication) 0 0 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...nonnegative integers greatest common divisor Greatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...1 n-by-n square matrices Matrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...· (multiplication) matrix of all zeroes extended real numbers minimum/infimum −∞ extended real numbers maximum/supremum +∞ sets ∩ (intersection) { } (empty set Empty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
)subsets of a set M ∪ (union) M boolean logic Boolean logicBoolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
∧ (logical and) ⊥ (falsity) boolean logic Boolean logicBoolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
∨ (logical or) ⊤ (truth)
External links
- Absorbing element at PlanetMath