Semiring
Encyclopedia
In abstract algebra
, a semiring is an algebraic structure
similar to a ring, but without the requirement that each element must have an additive inverse
. The term rig is also used occasionally—this originated as a joke, suggesting that rigs are rings without negative elements.
s + and ·, called addition and multiplication, such that:
This last axiom
is omitted from the definition of a ring: it follows automatically from the other ring axioms. Here it does not, and it is necessary to state it in the definition.
The difference between rings and semirings, then, is that addition yields only a commutative monoid, not necessarily a commutative group. Specifically, elements in semirings do not necessarily have an inverse for the addition.
The symbol · is usually omitted from the notation; that is, a·b is just written ab. Similarly, an order of operations
is accepted, according to which · is applied before +; that is, is
A commutative semiring is one whose multiplication is commutative. An idempotent semiring (also known as a dioid) is one whose addition is idempotent: a + a = a, that is, (R, +, 0) is a join-semilattice with zero.
There are some authors who prefer to leave out the requirement that a semiring have a 0 or 1. This makes the analogy between ring and semiring on the one hand and group
and semigroup
on the other hand work more smoothly. These authors often use rig for the concept defined here.
In particular, one can generalise the theory of algebras
over commutative ring
s directly to a theory of algebras over commutative semirings.
Then a ring is simply an algebra over the commutative semiring Z of integer
s.
Some mathematicians go so far as to say that semirings are really the more fundamental concept, and specialising to rings should be seen in the same light as specialising to, say, algebras over the complex number
s.
Idempotent semirings are special to semiring theory as any ring which is idempotent under addition is trivial. One can define a partial order ≤ on an idempotent semiring by setting a ≤ b whenever a + b = b (or, equivalently, if there exists an x such that a + x = b). It is easy to see that 0 is the least element with respect to this order: 0 ≤ a for all a. Addition and multiplication respect the ordering in the sense that a ≤ b implies ac ≤ bc and ca ≤ cb and (a+c) ≤ (b+c).
does not require addition to be commutative, nor does it require right-distributivity. Just as cardinal numbers form a semiring, so do ordinal number
s form a near-ring.
In category theory
, a 2-ring is a category with functor
ial operations analogous to those of a ring. That the cardinal numbers form a ring can be categorified to say that the category of sets
(or more generally, any topos
) is a 2-ring.
on discrete event systems. The real numbers then are the "costs" or "arrival time"; the "max" operation corresponds to having to wait for all prerequisites of an events (thus taking the maximal time) while the "min" operation corresponds to being able to choose the best, less costly choice; and + corresponds to accumulation along the same path.
The Floyd-Warshall algorithm
for shortest paths can thus be reformulated as a computation over a (min, +) algebra. Similarly, the Viterbi algorithm
for finding the most probable state sequence corresponding to an observation sequence in a Hidden Markov model
can also be formulated as a computation over a (max, ×) algebra on probabilities. These dynamic programming
algorithms rely on the distributive property of their associated semirings to compute quantities over a large (possibly exponential) number of terms more efficiently than enumerating each of them.
Such semirings are used in measure theory. An example of a semiring of sets is the collection of half-open, half-closed real intervals
.
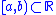Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a semiring is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
similar to a ring, but without the requirement that each element must have an additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
. The term rig is also used occasionally—this originated as a joke, suggesting that rigs are rings without negative elements.
Definition
A semiring is a set R equipped with two binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s + and ·, called addition and multiplication, such that:
- (R, +) is a commutative monoid with identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
0:- (a + b) + c = a + (b + c)
- 0 + a = a + 0 = a
- a + b = b + a
- (R, ·) is a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
with identity element 1:- (a·b)·c = a·(b·c)
- 1·a = a·1 = a
- Multiplication distributes over addition:
- a·(b + c) = (a·b) + (a·c)
- (a + b)·c = (a·c) + (b·c)
- 0 annihilates R, with respect to multiplication:
- 0·a = a·0 = 0
This last axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
is omitted from the definition of a ring: it follows automatically from the other ring axioms. Here it does not, and it is necessary to state it in the definition.
The difference between rings and semirings, then, is that addition yields only a commutative monoid, not necessarily a commutative group. Specifically, elements in semirings do not necessarily have an inverse for the addition.
The symbol · is usually omitted from the notation; that is, a·b is just written ab. Similarly, an order of operations
Order of operations
In mathematics and computer programming, the order of operations is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression....
is accepted, according to which · is applied before +; that is, is
A commutative semiring is one whose multiplication is commutative. An idempotent semiring (also known as a dioid) is one whose addition is idempotent: a + a = a, that is, (R, +, 0) is a join-semilattice with zero.
There are some authors who prefer to leave out the requirement that a semiring have a 0 or 1. This makes the analogy between ring and semiring on the one hand and group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
on the other hand work more smoothly. These authors often use rig for the concept defined here.
In general
- Any ring is also a semiring.
- The idealsIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of a ring form a semiring under addition and multiplication of ideals. - Any unital, quantaleQuantaleIn mathematics, quantales are certain partially ordered algebraic structures that generalize locales as well as various multiplicative lattices of ideals from ring theory and functional analysis...
is an idempotent semiring, or dioid, under join and multiplication. - Any bounded, distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
is a commutative, idempotent semiring under join and meet. - In particular, a Boolean algebra is such a semiring. A Boolean ringBoolean ringIn mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
is also a semiring—indeed, a ring—but it is not idempotent under addition. - A normal skew latticeSkew latticeIn abstract algebra, a skew lattice is an algebraic structure that is a non-commutative generalization of a lattice. While the term skew lattice can be used to refer to any non-commutative generalization of a lattice, over the past twenty years it has been used primarily as follows.-Definition:A...
in a ring R is an idempotent semiring for the operations multiplication and nabla, where the latter operation is defined by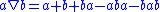
. - A Kleene algebraKleene algebraIn mathematics, a Kleene algebra is either of two different things:* A bounded distributive lattice with an involution satisfying De Morgan's laws , additionally satisfying the inequality x∧−x ≤ y∨−y. Kleene algebras are subclasses of Ockham algebras...
is an idempotent semiring R with an additional unary operator * : R → R called the Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
. Kleene algebras are important in the theory of formal languageFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s and regular expressionRegular expressionIn computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
s.
Specific examples
- The motivating example of a semiring is the set of natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s N (including zero0 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
) under ordinary addition and multiplication. Likewise, the non-negative rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s and the non-negative real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s form semirings. All these semirings are commutative. - The square n-by-n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with non-negative entries form a (non-commutative) semiring under ordinary addition and multiplication of matrices. More generally, this likewise applies to the square matrices whose entries are elements of any other given semiring S, and the semiring is generally non-commutative even though S may be commutative. - If A is a commutative monoid, the set End(A) of endomorphismEndomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s f:A→A form a semiring, where addition is pointwise addition and multiplication is function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. The zero morphismZero morphismIn category theory, a zero morphism is a special kind of morphism exhibiting properties like those to and from a zero object.Suppose C is a category, and f : X → Y is a morphism in C...
and the identity are the respective neutral elements. If A is the additive monoid of natural numbers we obtain the semiring of natural numbers as End(A), and if A=S^n with S a semiring, we obtain (after associating each morphism to a matrix) the semiring of square n-by-n matrices with coefficients in S. - The simplest example of a semiring which is not a ring is the commutative semiring B formed by the two-element Boolean algebra.
- N[x], polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with natural number coefficients form a commutative semiring. In fact, this is the freeFree objectIn mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
commutative semiring on a single generator {x}. - Of course, rings such as the integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s are also examples of semirings. - The tropical semiring, R ∪ {−∞}, is a commutative, idempotent semiring with max(a,b) serving as semiring addition (identity −∞) and ordinary addition (identity 0) serving as semiring multiplication. In an alternative formulation, the tropical semiring is R ∪ {∞}, and min replaces max as the addition operation.
- The set of cardinal numberCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s smaller than any given infinite cardinal form a semiring under cardinal addition and multiplication. The set of all cardinals of an inner modelInner modelIn mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
form a semiring under (inner model) cardinal addition and multiplication.
Semiring theory
Much of the theory of rings continues to make sense when applied to arbitrary semirings.In particular, one can generalise the theory of algebras
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
over commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s directly to a theory of algebras over commutative semirings.
Then a ring is simply an algebra over the commutative semiring Z of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
Some mathematicians go so far as to say that semirings are really the more fundamental concept, and specialising to rings should be seen in the same light as specialising to, say, algebras over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Idempotent semirings are special to semiring theory as any ring which is idempotent under addition is trivial. One can define a partial order ≤ on an idempotent semiring by setting a ≤ b whenever a + b = b (or, equivalently, if there exists an x such that a + x = b). It is easy to see that 0 is the least element with respect to this order: 0 ≤ a for all a. Addition and multiplication respect the ordering in the sense that a ≤ b implies ac ≤ bc and ca ≤ cb and (a+c) ≤ (b+c).
Further generalizations
A near-ringNear-semiring
In mathematics, a near-semiring is an algebraic structure more general to near-ring and semiring. Near-semirings arise naturally from functions on semigroups.- Definition :...
does not require addition to be commutative, nor does it require right-distributivity. Just as cardinal numbers form a semiring, so do ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s form a near-ring.
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a 2-ring is a category with functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
ial operations analogous to those of a ring. That the cardinal numbers form a ring can be categorified to say that the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
(or more generally, any topos
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
) is a 2-ring.
Applications
Dioids, especially the (max, +) and (min, +) dioids on the reals, are often used in performance evaluationPerformance Evaluation
Performance Evaluation is an international journal published by Elsevier. The current Editor-in-chief is Philippe Nain. The journal was previously published by North-Holland Publisher.-Editors:*1981–1986 Hisashi Kobayashi*1987–1990 Martin Reiser...
on discrete event systems. The real numbers then are the "costs" or "arrival time"; the "max" operation corresponds to having to wait for all prerequisites of an events (thus taking the maximal time) while the "min" operation corresponds to being able to choose the best, less costly choice; and + corresponds to accumulation along the same path.
The Floyd-Warshall algorithm
Floyd-Warshall algorithm
In computer science, the Floyd–Warshall algorithm is a graph analysis algorithm for finding shortest paths in a weighted graph and also for finding transitive closure of a relation R...
for shortest paths can thus be reformulated as a computation over a (min, +) algebra. Similarly, the Viterbi algorithm
Viterbi algorithm
The Viterbi algorithm is a dynamic programming algorithm for finding the most likely sequence of hidden states – called the Viterbi path – that results in a sequence of observed events, especially in the context of Markov information sources, and more generally, hidden Markov models...
for finding the most probable state sequence corresponding to an observation sequence in a Hidden Markov model
Hidden Markov model
A hidden Markov model is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E...
can also be formulated as a computation over a (max, ×) algebra on probabilities. These dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
algorithms rely on the distributive property of their associated semirings to compute quantities over a large (possibly exponential) number of terms more efficiently than enumerating each of them.
Semiring of sets
A semiring (of sets) is a non-empty collection S of sets such that-
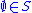
- If
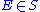and 
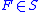then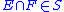 
. - If
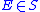and 
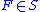then there exists a finite number of mutually disjoint sets 
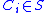for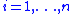 
such that 
.
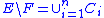Such semirings are used in measure theory. An example of a semiring of sets is the collection of half-open, half-closed real intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
.
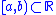