Free object
Encyclopedia
In mathematics
, the idea of a free object is one of the basic concepts of abstract algebra
. It is a part of universal algebra
, in the sense that it relates to all types of algebraic structure (with finitary
operations). It also has a formulation in terms of category theory
, although this is in yet more abstract terms. Examples include free group
s, tensor algebra
s, or free lattice
s. Informally, a free object over a set A can be thought as being a "generic" algebraic structure over A: the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure.
of the notion of basis
in a vector space. A linear function u : E1 → E2 between vector spaces is entirely determined by its values on a basis of the vector space E1. Conversely, a function u : E1 → E2 defined on a basis of E1 can be uniquely extended to a linear function. The following definition translates this to any category.
Let (C,F) be a concrete category
(i.e. F: C → Set is a faithful functor), let X be a set (called basis), A ∈ C an object, and i: X → F(A) a map between sets (called canonical injection). We say that A is the free object on X (with respect to i) if and only if they satisfy this universal property
:
This way the free functor that builds the free object A from the set X becomes left adjoint to the forgetful functor
.
s formed from an alphabet. Then one imposes a set of equivalence relation
s upon the words, where the relations are the defining relations of the algebraic object at hand. The free object then consists of the set of equivalence classes.
Consider, for example, the construction of the free group in two generators. One starts with an alphabet consisting of the five letters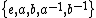
. In the first step, there is not yet any assigned meaning to the "letters" 
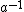or 
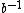; these will be given later, in the second step. Thus, one could equally well start with the alphabet in five letters that is 
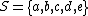. In this example, the set of all words or strings 
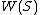will include strings such as aebecede and abdc, and so on, of arbitrary finite length, with the letters arranged in every possible order.
In the next step, one imposes a set of equivalence relations. The equivalence relations for a group
are that of multiplication by the identity,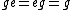
, and the multiplication of inverses: 
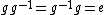. Applying these relations to the strings above, one obtains
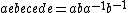
where it was understood that c is a stand-in for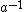
, and d is a stand-in for 
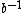, while e is the identity element. Similarly, one has
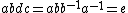
Denoting the equivalence relation or congruence
by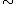
, the free object is then the collection of equivalence classes of words. Thus, in this example, the free group in two generators is the quotient
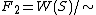
This is often written as
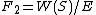
where
is the set of all words, and
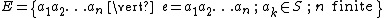
is the equivalence class of the identity, after the relations defining a group are imposed.
A simpler example are the free monoids. The free monoid on a set X, is the monoid of all finite strings
using X as alphabet, with operation concatenation
of strings. The identity is the empty string. In essence, the free monoid is simply the set of all words, with no equivalence relations imposed. This example is developed further in the article on the Kleene star
.
or a free magma; the leaves of the tree are the letters from the alphabet.
The algebraic relations may then be general arities
or finitary relations on the leaves of the tree. Rather than starting with the collection of all possible parenthesized strings, it can be more convenient to start with the Herbrand universe. Properly describing or enumerating the contents of a free object can be easy or difficult, depending on the particular algebraic object in question. For example, the free group in two generators is easily described. By contrast, little or nothing is known about the structure of free Heyting algebras in more than one generator. The problem of determining if two different strings belong to the same equivalence class is known as the word problem
.
As the examples suggest, free objects look like constructions from syntax
; one may reverse that to some extent by saying that major uses of syntax can be explained and characterised as free objects, in a way that makes apparently heavy 'punctuation' explicable (and more memorable).
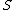be any set, let 
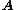be an algebraic structure
of type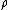
generated by 
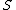. Let the underlying set of this algebraic structure 
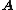, sometimes called universe, be 
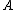, and let 
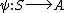be a function. We say that 
,
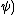(or informally just 
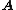) is a free algebra (of type 
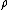) on the set 
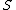of free generators if, for every algebra 
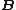of type 
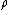and function 
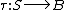, where 
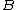is a universe of 
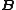, there exists a unique homomorphism 
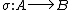such that 
.
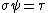, where one defines a functor
, the free functor, that is the left adjoint to the forgetful functor
.
Consider the category C of algebraic structure
s; these can be thought of as sets plus operations, obeying some laws. This category has a functor,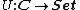
, the forgetful functor
, which maps objects and functions in C to Set, the category of sets
. The forgetful functor is very simple: it just ignores all of the operations.
The free functor F, when it exists, is the left adjoint to U. That is,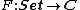
takes sets X in Set to their corresponding free objects F(X) in the category C. The set X can be thought of as the set of "generators" of the free object F(X).
For the free functor to be a left adjoint, one must also have a C-morphism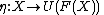
. More explicitly, F is, up to isomorphisms in C, characterized by the following universal property
:
Concretely, this sends a set into the free object on that set; it's the "inclusion of a basis". Abusing notation,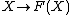
(this abuses notation because X is a set, while F(X) is an algebra; correctly, it is 
).
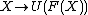The natural transformation
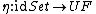is called the unit; together with the counit 
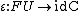, one may construct a T-algebra, and so a monad
. This leads to the next topic: free functors exist when C is a monad over Set.
Here, a variety is a synonym for a finitary algebraic category, thus implying that the set of relations are finitary, and algebraic because it is monadic
over Set.
For example the tensor algebra
construction on a vector space
as left adjoint to the functor on associative algebra
s that ignores the algebra structure. It is therefore often also called a free algebra
.
Likewise the symmetric algebra
and exterior algebra
are free symmetric and anti-symmetric algebras on a vector space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the idea of a free object is one of the basic concepts of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. It is a part of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, in the sense that it relates to all types of algebraic structure (with finitary
Finitary
In mathematics or logic, a finitary operation is one, like those of arithmetic, that takes a finite number of input values to produce an output. An operation such as taking an integral of a function, in calculus, is defined in such a way as to depend on all the values of the function , and is so...
operations). It also has a formulation in terms of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, although this is in yet more abstract terms. Examples include free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s, tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
s, or free lattice
Free lattice
In mathematics, in the area of order theory, a free lattice is the free object corresponding to a lattice. As free objects, they have the universal property. The word problem for free lattices is also challenging.-Formal definition:...
s. Informally, a free object over a set A can be thought as being a "generic" algebraic structure over A: the only equations that hold between elements of the free object are those that follow from the defining axioms of the algebraic structure.
Definition
Free objects are the direct generalization to categoriesCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of the notion of basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
in a vector space. A linear function u : E1 → E2 between vector spaces is entirely determined by its values on a basis of the vector space E1. Conversely, a function u : E1 → E2 defined on a basis of E1 can be uniquely extended to a linear function. The following definition translates this to any category.
Let (C,F) be a concrete category
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
(i.e. F: C → Set is a faithful functor), let X be a set (called basis), A ∈ C an object, and i: X → F(A) a map between sets (called canonical injection). We say that A is the free object on X (with respect to i) if and only if they satisfy this universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
:
- for any object B and any map between sets f: X → F(B), there exists a unique morphism
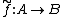such that 
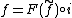. That is, the following diagram commutes:
This way the free functor that builds the free object A from the set X becomes left adjoint to the forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
.
Examples
The creation of free objects proceeds in two steps. For algebras that conform to the associative law, the first step is to consider the collection of all possible wordString (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
s formed from an alphabet. Then one imposes a set of equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s upon the words, where the relations are the defining relations of the algebraic object at hand. The free object then consists of the set of equivalence classes.
Consider, for example, the construction of the free group in two generators. One starts with an alphabet consisting of the five letters
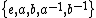. In the first step, there is not yet any assigned meaning to the "letters" 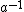or 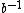; these will be given later, in the second step. Thus, one could equally well start with the alphabet in five letters that is 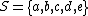. In this example, the set of all words or strings 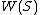will include strings such as aebecede and abdc, and so on, of arbitrary finite length, with the letters arranged in every possible order.In the next step, one imposes a set of equivalence relations. The equivalence relations for a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
are that of multiplication by the identity,
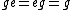, and the multiplication of inverses: 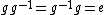. Applying these relations to the strings above, one obtains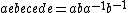where it was understood that c is a stand-in for
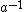, and d is a stand-in for 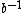, while e is the identity element. Similarly, one has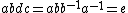Denoting the equivalence relation or congruence
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
by
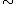, the free object is then the collection of equivalence classes of words. Thus, in this example, the free group in two generators is the quotientQuotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
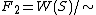
This is often written as
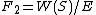
where
is the set of all words, and
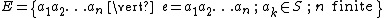
is the equivalence class of the identity, after the relations defining a group are imposed.
A simpler example are the free monoids. The free monoid on a set X, is the monoid of all finite strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
using X as alphabet, with operation concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
of strings. The identity is the empty string. In essence, the free monoid is simply the set of all words, with no equivalence relations imposed. This example is developed further in the article on the Kleene star
Kleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
.
General case
In the general case, the algebraic relations need not be associative, in which case the starting point is not the set of all words, but rather, strings punctuated with parentheses, which are used to indicate the non-associative groupings of letters. Such a string may equivalently be represented by a binary treeBinary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
or a free magma; the leaves of the tree are the letters from the alphabet.
The algebraic relations may then be general arities
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
or finitary relations on the leaves of the tree. Rather than starting with the collection of all possible parenthesized strings, it can be more convenient to start with the Herbrand universe. Properly describing or enumerating the contents of a free object can be easy or difficult, depending on the particular algebraic object in question. For example, the free group in two generators is easily described. By contrast, little or nothing is known about the structure of free Heyting algebras in more than one generator. The problem of determining if two different strings belong to the same equivalence class is known as the word problem
Word problem (mathematics)
In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
.
As the examples suggest, free objects look like constructions from syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
; one may reverse that to some extent by saying that major uses of syntax can be explained and characterised as free objects, in a way that makes apparently heavy 'punctuation' explicable (and more memorable).
Free universal algebras
Let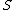 be any set, let 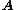be an algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
of type
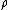generated by 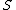. Let the underlying set of this algebraic structure 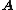, sometimes called universe, be 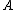, and let 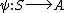be a function. We say that , 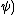(or informally just 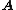) is a free algebra (of type 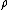) on the set 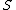of free generators if, for every algebra 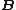of type 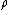and function 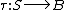, where 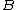is a universe of 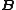, there exists a unique homomorphism 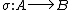such that 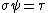.Free functor
The most general setting for a free object is in category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, where one defines a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
, the free functor, that is the left adjoint to the forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
.
Consider the category C of algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s; these can be thought of as sets plus operations, obeying some laws. This category has a functor,
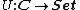, the forgetful functorForgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
, which maps objects and functions in C to Set, the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. The forgetful functor is very simple: it just ignores all of the operations.
The free functor F, when it exists, is the left adjoint to U. That is,
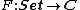takes sets X in Set to their corresponding free objects F(X) in the category C. The set X can be thought of as the set of "generators" of the free object F(X).For the free functor to be a left adjoint, one must also have a C-morphism
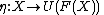. More explicitly, F is, up to isomorphisms in C, characterized by the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
:
- Whenever A is an algebra in C, and g: X→U(A) is a function (a morphism in the category of sets), then there is a unique C-morphism h: F(X)→A such that U(h)oη = g.
Concretely, this sends a set into the free object on that set; it's the "inclusion of a basis". Abusing notation,
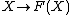(this abuses notation because X is a set, while F(X) is an algebra; correctly, it is 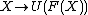).The natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
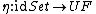is called the unit; together with the counit 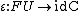, one may construct a T-algebra, and so a monadMonad (category theory)
In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
. This leads to the next topic: free functors exist when C is a monad over Set.
Existence
There are general existence theorems that apply; the most basic of them guarantees that- Whenever C is a varietyVariety (universal algebra)In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
, then for every set X there is a free object F(X) in C.
Here, a variety is a synonym for a finitary algebraic category, thus implying that the set of relations are finitary, and algebraic because it is monadic
Monad (category theory)
In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
over Set.
General case
Other types of forgetfulness also give rise to objects quite like free objects, in that they are left adjoint to a forgetful functor, not necessarily to sets.For example the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
construction on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
as left adjoint to the functor on associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s that ignores the algebra structure. It is therefore often also called a free algebra
Free algebra
In mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring .-Definition:...
.
Likewise the symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
and exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
are free symmetric and anti-symmetric algebras on a vector space.
List of free objects
Specific kinds of free objects include:- free algebraFree algebraIn mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring .-Definition:...
- free associative algebra
- free commutative algebra
- free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
- free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
- free abelian group
- free Kleene algebra
- free latticeFree latticeIn mathematics, in the area of order theory, a free lattice is the free object corresponding to a lattice. As free objects, they have the universal property. The word problem for free lattices is also challenging.-Formal definition:...
- free Boolean algebraFree Boolean algebraIn abstract algebra, a branch of mathematics, a free Boolean algebra is a Boolean algebra 〈B,F〉, such that the set B has a subset whose elements are called generators...
- free distributive lattice
- free Heyting algebra
- free Boolean algebra
- free Lie algebraFree Lie algebraIn mathematics, a free Lie algebra, over a given field K, is a Lie algebra generated by a set X, without any imposed relations.-Definition:Given a set X, one can show that there exists a unique free Lie algebra L generated by X....
- free magma
- free moduleFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
- free monoid
- free commutative monoid
- free ring
- free semigroupFree semigroupIn abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
- free semiring
- free commutative semiring
- free theory
- term algebraTerm algebraIn universal algebra and mathematical logic, a term algebra is a freely generated algebraic structure over a given signature. For example, in a signature consisting of a single binary operation, the term algebra over a set X of variables is exactly the free magma generated by X...