
Free Lie algebra
Encyclopedia
In mathematics
, a free Lie algebra, over a given field
K, is a Lie algebra
generated by a set X, without any imposed relations.
Given a set X, one can show that there exists a unique free Lie algebra L(X) generated by X.
In the language of category theory, the functor
sending a set X to the Lie algebra generated by X is the free functor from the category of sets to the category of Lie algebras. That is, it is left adjoint to the forgetful functor
.
As the 0-graded component of the free Lie algebra on a set X is just the free vector space on that group, one can alternatively define a free Lie algebra on a vector space V as left adjoint to the forgetful functor from Lie algebras over a field K to vector spaces over the field K – forgetting the Lie algebra structure, but remembering the vector space structure.
of a free Lie algebra on a set X is the free associative algebra generated by X. By the Poincaré-Birkhoff-Witt theorem it is the "same size" as the symmetric algebra of the free Lie algebra (meaning that if both sides are graded by giving elements of X degree 1 then they are isomorphic as graded vector spaces). This can be used to describe the dimension of the piece of the free Lie algebra of any given degree.
Witt showed that the number of basic commutators of degree k in the free Lie algebra on an m-element set is given by the necklace polynomial: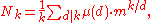
where is the Möbius function
is the Möbius function
.
The graded dual of the universal enveloping algebra of a free Lie algebra on a finite set is the shuffle algebra
.
s, with their leaves labelled by elements of X. Hall sets were introduced by based on work of Philip Hall
on groups. Subsequently Wilhelm Magnus
showed that they arise as the graded Lie algebra
associated with the filtration on a free group
given by the lower central series. This correspondence was motivated by commutator
identities in group theory
due to Philip Hall and Ernst Witt
.
s, called the Lyndon basis. (This is also called the Chen–Fox–Lyndon basis or the Lyndon–Shirshov basis, and is essentially the same as the Shirshov basis.)
There is a bijection γ from the Lyndon words in an ordered alphabet to a basis of the free Lie algebra on this alphabet defined as follows.
are related to the free Lie algebra, as discussed in that article.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a free Lie algebra, over a given field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, is a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
generated by a set X, without any imposed relations.
Definition
- Let X be a set and i: X → L a morphism of sets from X into a Lie algebra L. The Lie algebra L is called free on X if for any Lie algebra A with a morphism of sets f: X → A, there is a unique Lie algebra morphism g: L → A such that f = g o i.
Given a set X, one can show that there exists a unique free Lie algebra L(X) generated by X.
In the language of category theory, the functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
sending a set X to the Lie algebra generated by X is the free functor from the category of sets to the category of Lie algebras. That is, it is left adjoint to the forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
.
As the 0-graded component of the free Lie algebra on a set X is just the free vector space on that group, one can alternatively define a free Lie algebra on a vector space V as left adjoint to the forgetful functor from Lie algebras over a field K to vector spaces over the field K – forgetting the Lie algebra structure, but remembering the vector space structure.
Universal enveloping algebra
The universal enveloping algebraUniversal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of a free Lie algebra on a set X is the free associative algebra generated by X. By the Poincaré-Birkhoff-Witt theorem it is the "same size" as the symmetric algebra of the free Lie algebra (meaning that if both sides are graded by giving elements of X degree 1 then they are isomorphic as graded vector spaces). This can be used to describe the dimension of the piece of the free Lie algebra of any given degree.
Witt showed that the number of basic commutators of degree k in the free Lie algebra on an m-element set is given by the necklace polynomial:
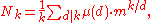
where
 is the Möbius function
is the Möbius functionMöbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
The graded dual of the universal enveloping algebra of a free Lie algebra on a finite set is the shuffle algebra
Shuffle algebra
In mathematics, a shuffle algebra is a Hopf algebra with a basis corresponding to words on some set, whose product is given by the shuffle product XшY of two words X, Y: the sum of all ways of interlacing them. The shuffle product was introduced by...
.
Hall sets
An explicit basis of the free Lie algebra can be given in terms of a Hall set, which is a particular kind of subset inside the free magma on X. Elements of the free magma are binary treeBinary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
s, with their leaves labelled by elements of X. Hall sets were introduced by based on work of Philip Hall
Philip Hall
Philip Hall FRS , was an English mathematician.His major work was on group theory, notably on finite groups and solvable groups.-Biography:...
on groups. Subsequently Wilhelm Magnus
Wilhelm Magnus
Wilhelm Magnus was a mathematician. He made important contributions in combinatorial group theory, Lie algebras, mathematical physics, elliptic functions, and the study of tessellations....
showed that they arise as the graded Lie algebra
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
associated with the filtration on a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
given by the lower central series. This correspondence was motivated by commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
identities in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
due to Philip Hall and Ernst Witt
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
.
Lyndon basis
In particular there is a basis of the free Lie algebra corresponding to Lyndon wordLyndon word
In mathematics, in the areas of combinatorics and computer science, a Lyndon word is a string that is strictly smaller in lexicographic order than all of its rotations...
s, called the Lyndon basis. (This is also called the Chen–Fox–Lyndon basis or the Lyndon–Shirshov basis, and is essentially the same as the Shirshov basis.)
There is a bijection γ from the Lyndon words in an ordered alphabet to a basis of the free Lie algebra on this alphabet defined as follows.
- If a word w has length 1 then γ(w)=w (considered as a generator of the free Lie algebra).
- If w has length at least 2, then write w=uv for Lyndon words u, v with v as long as possible. Then γ(w) = [γ(u),γ(v)]
Shirshov–Witt theorem
and showed that any Lie subalgebra of a free Lie algebra is itself a free Lie algebra.Applications
The Milnor invariants of the link groupLink group
In knot theory, an area of mathematics, the link group of a link is an analog of the knot group of a knot. They were described by John Milnor in his Bachelor's thesis, .- Definition :...
are related to the free Lie algebra, as discussed in that article.

