Link group
Encyclopedia
In knot theory
, an area of mathematics
, the link group of a link
is an analog of the knot group
of a knot
. They were described by John Milnor
in his Bachelor's thesis, .
The link group of an n-component link is essentially the set of (n + 1)-component links extending this link, up to link homotopy. In other words, each component of the extended link is allowed to move through regular homotopy
(homotopy through immersions), knotting or unknotting itself, but is not allowed to move through other component. This is a weaker condition than isotopy: for example, the Whitehead link
has linking number
0, and thus is link homotopic to the unlink
, but it is not isotopic
to the unlink.
It is not the fundamental group
of the link complement, since the components of the link are allowed to move through themselves, though not each other, but thus is a quotient group
of the link complement, since one can start with this, and then by knotting or unknotting components, some of these elements may become equivalent to each other.
on n generators,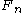
, as the link group of a single link is the knot group
of the unknot
, which is the integers, and the link group of an unlinked union is the free product
of the link groups of the components.
The link group of the Hopf link
, the simplest non-trivial link – two circles, linked once – is the free abelian group
on two generators,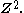
Note that the link group of two unlinked circles is the free nonabelian group on two generators, of which the free abelian group on two generators is a quotient
. In this case the link group is the fundamental group of the link complement, as the link complement deformation retracts onto a torus.
The Whitehead link
is link homotopic to the unlink – though it is not isotopic to the unlink – and thus has link group the free group on two generators.
which have thus come to be called "Milnor's μ-bar invariants", or simply the "Milnor invariants". For each k, there is an k-ary function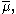 
which defines invariants according to which k of the links one selects, in which order.
Milnor's invariants can be related to Massey product
s on the link complement (the complement of the link); this was suggested in , and made precise in and .
As with Massey products, the Milnor invariants of length k + 1 are defined if all Milnor invariants of length less than or equal to k vanish. The first (2-fold) Milnor invariant is simply the linking number (just as the 2-fold Massey product is the cup product, which is dual to intersection), while the 3-fold Milnor invariant measures whether 3 pairwise unlinked circles are Borromean rings, and if so, in some sense, how many times (i.e., Borromean rings have a Milnor 3-fold invariant of 1 or –1, depending on order, but other 3-element links can have an invariant of 2 or more, just as linking numbers can be greater than 1).
Another definition is the following: let's consider a link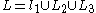
. Suppose that 
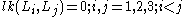. Find any Seifert surfaces for link components- 
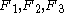correspondingly, such that 
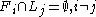. Then the Milnor 3-fold invariant equals the number of triple points in 
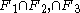counting with signs.
Milnor invariants can sometimes be defined if the lower order invariants do not vanish, but then there is an indeterminacy, which depends on the values of the lower order invariants. This failure to be determined or indeterminacy can be understood two ways: algebraically, it is due to the indeterminacy of Massey products if lower order Massey products do not vanish; geometrically, it is due to the indeterminacy in expressing a link as a closed string link, as discussed below.
Milnor invariants can be considered as invariants of string links, in which case they are universally defined, and the indeterminacy of the Milnor invariant of a link is precisely due to the multiple ways that a given links can be cut into a string link; this allows the classification of links up to link homotopy, as in . Viewed from this point of view, Milnor invariants are finite type invariant
s, and in fact they (and their products) are the only rational finite type concordance invariants of string links; .
The number of linearly independent Milnor invariants of length k+1 is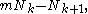
where 
is the number of basic commutators of length k in the free Lie algebra
, namely: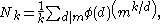
where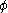
is the Möbius function
, which was shown in . This grows on the order of
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, an area of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the link group of a link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
is an analog of the knot group
Knot group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....
of a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
. They were described by John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
in his Bachelor's thesis, .
Definition
Regular homotopy
In the mathematical field of topology, a regular homotopy refers to a special kind of homotopy between immersions of one manifold in another. The homotopy must be a 1-parameter family of immersions....
(homotopy through immersions), knotting or unknotting itself, but is not allowed to move through other component. This is a weaker condition than isotopy: for example, the Whitehead link
Whitehead link
In knot theory, the Whitehead link, discovered by J.H.C. Whitehead, is one of the most basic links.J.H.C. Whitehead spent much of the 1930s looking for a proof of the Poincaré conjecture...
has linking number
Linking number
In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other...
0, and thus is link homotopic to the unlink
Unlink
In the mathematical field of knot theory, the unlink is a link that is equivalent to finitely many disjoint circles in the plane.- Properties :...
, but it is not isotopic
Isotopic
The word isotopic has a number of different meanings, including:* In the physical sciences, to do with chemical isotopes;* In mathematics, to do with a relation called isotopy.* In geometry, isotopic refers to facet-transitivity....
to the unlink.
It is not the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the link complement, since the components of the link are allowed to move through themselves, though not each other, but thus is a quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of the link complement, since one can start with this, and then by knotting or unknotting components, some of these elements may become equivalent to each other.
Examples
The link group of the n-component unlink is the free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on n generators,
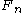, as the link group of a single link is the knot groupKnot group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....
of the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
, which is the integers, and the link group of an unlinked union is the free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
of the link groups of the components.
Hopf link
thumb|right|[[Skein relation]] for the Hopf link.In mathematical knot theory, the Hopf link, named after Heinz Hopf, is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly once...
, the simplest non-trivial link – two circles, linked once – is the free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
on two generators,
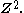Note that the link group of two unlinked circles is the free nonabelian group on two generators, of which the free abelian group on two generators is a quotientQuotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
. In this case the link group is the fundamental group of the link complement, as the link complement deformation retracts onto a torus.
The Whitehead link
Whitehead link
In knot theory, the Whitehead link, discovered by J.H.C. Whitehead, is one of the most basic links.J.H.C. Whitehead spent much of the 1930s looking for a proof of the Poincaré conjecture...
is link homotopic to the unlink – though it is not isotopic to the unlink – and thus has link group the free group on two generators.
Milnor invariants
Milnor defined invariants of a link (functions on the link group) in , using the character which have thus come to be called "Milnor's μ-bar invariants", or simply the "Milnor invariants". For each k, there is an k-ary function 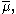which defines invariants according to which k of the links one selects, in which order.Milnor's invariants can be related to Massey product
Massey product
In algebraic topology, the Massey product is a cohomology operation of higher order introduced in , which generalizes the cup product.-Massey triple product:...
s on the link complement (the complement of the link); this was suggested in , and made precise in and .
As with Massey products, the Milnor invariants of length k + 1 are defined if all Milnor invariants of length less than or equal to k vanish. The first (2-fold) Milnor invariant is simply the linking number (just as the 2-fold Massey product is the cup product, which is dual to intersection), while the 3-fold Milnor invariant measures whether 3 pairwise unlinked circles are Borromean rings, and if so, in some sense, how many times (i.e., Borromean rings have a Milnor 3-fold invariant of 1 or –1, depending on order, but other 3-element links can have an invariant of 2 or more, just as linking numbers can be greater than 1).
Another definition is the following: let's consider a link
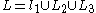. Suppose that 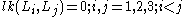. Find any Seifert surfaces for link components- 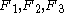correspondingly, such that 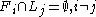. Then the Milnor 3-fold invariant equals the number of triple points in 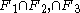counting with signs.Milnor invariants can sometimes be defined if the lower order invariants do not vanish, but then there is an indeterminacy, which depends on the values of the lower order invariants. This failure to be determined or indeterminacy can be understood two ways: algebraically, it is due to the indeterminacy of Massey products if lower order Massey products do not vanish; geometrically, it is due to the indeterminacy in expressing a link as a closed string link, as discussed below.
Milnor invariants can be considered as invariants of string links, in which case they are universally defined, and the indeterminacy of the Milnor invariant of a link is precisely due to the multiple ways that a given links can be cut into a string link; this allows the classification of links up to link homotopy, as in . Viewed from this point of view, Milnor invariants are finite type invariant
Finite type invariant
In the mathematical theory of knots, a finite type invariant is a knot invariant that can be extended to an invariant of certain singular knots that vanishes on singular knots with m + 1 singularities and does not vanish on some singular knot with 'm' singularities...
s, and in fact they (and their products) are the only rational finite type concordance invariants of string links; .
The number of linearly independent Milnor invariants of length k+1 is
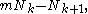where is the number of basic commutators of length k in the free Lie algebraFree Lie algebra
In mathematics, a free Lie algebra, over a given field K, is a Lie algebra generated by a set X, without any imposed relations.-Definition:Given a set X, one can show that there exists a unique free Lie algebra L generated by X....
, namely:
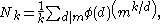
where
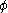is the Möbius functionMöbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
, which was shown in . This grows on the order of