
Knot (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a knot is an embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
in 3-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, R3, considered up to continuous deformations (isotopies
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
). A crucial difference between the standard mathematical and conventional notions of a knot
Knot
A knot is a method of fastening or securing linear material such as rope by tying or interweaving. It may consist of a length of one or several segments of rope, string, webbing, twine, strap, or even chain interwoven such that the line can bind to itself or to some other object—the "load"...
is that mathematical knots are closed—there are no ends to tie or untie on a mathematical knot. Physical properties such as friction and thickness also do not apply, although there are mathematical definitions of a knot that take such properties into account. The term knot is also applied to embeddings of
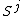 in
in 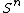 , especially in the case
, especially in the case 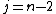 . The branch of mathematics that studies knots is known as knot theory
. The branch of mathematics that studies knots is known as knot theoryKnot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
.
Types of knots
The simplest knot, called the unknotUnknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
, is a round circle embedded in R3
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. In the ordinary sense of the word, the unknot is not "knotted" at all. The simplest nontrivial knots are the trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
(31 in the table), the figure-eight knot
Figure-eight knot (mathematics)
In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
(41) and the cinquefoil knot
Cinquefoil knot
In knot theory, the cinquefoil knot, also known as Solomon's seal knot or the pentafoil knot, is one of two knots with crossing number five, the other being the three-twist knot. It is listed as the 51 knot in the Alexander-Briggs notation, and can also be described as the -torus knot...
(51).
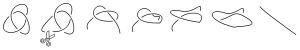
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
. Knots are links with a single component.
Often mathematicians prefer to consider knots embedded into the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
, S3, rather than R3 since the 3-sphere is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. The 3-sphere is equivalent to R3 with a single point added at infinity (see one-point compactification).

Solid torus
In mathematics, a solid torus is a topological space homeomorphic to S^1 \times D^2, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary...
,
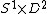 , into the 3-sphere. A knot is tame if and only if it can be represented as a finite closed polygonal chain
, into the 3-sphere. A knot is tame if and only if it can be represented as a finite closed polygonal chainPolygonal chain
A polygonal chain, polygonal curve, polygonal path, or piecewise linear curve, is a connected series of line segments. More formally, a polygonal chain P is a curve specified by a sequence of points \scriptstyle called its vertices so that the curve consists of the line segments connecting the...
. Knots that are not tame are called wild and can have pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
behavior. In knot theory and 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
theory, often the adjective "tame" is omitted. Smooth knots, for example, are always tame.
Given a knot in the 3-sphere, the knot complement
Knot complement
In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...
is all the points of the 3-sphere not contained in the knot. A major theorem of Gordon and Luecke states that at most two knots have homeomorphic complements (the original knot and its mirror reflection). This in effect turns the study of knots into the study of their complements, and in turn into 3-manifold theory.
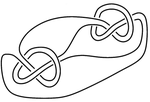
JSJ decomposition
In mathematics, the JSJ decomposition, also known as the toral decomposition, is a topological construct given by the following theorem:The acronym JSJ is for William Jaco, Peter Shalen, and Klaus Johannson...
and Thurston's hyperbolization theorem
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
reduces the study of knots in the 3-sphere to the study of various geometric manifolds via splicing or satellite operations.
Satellite knot
In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non-boundary parallel torus in its complement. The class of satellite knots include composite knots, cable knots and Whitehead doubles. A satellite knot K can be picturesquely described as follows:...
In the pictured knot, the JSJ-decomposition splits the complement into the union of three manifolds: two trefoil complements
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
and the complement of the Borromean rings
Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
. The trefoil complement has the geometry of
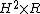 , while the Borromean rings complement has the geometry of
, while the Borromean rings complement has the geometry of 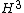 .
.Knots, more generally speaking
In contemporary mathematics the term knot is sometimes used to describe a more general phenomenon related to embeddings. Given a manifold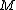 with a submanifold
with a submanifold 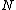 , one sometimes says
, one sometimes says 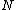 can be knotted in
can be knotted in  if there exists an embedding of
if there exists an embedding of  in
in 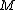 which is not isotopic to
which is not isotopic to 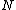 . Traditional knots form the case where
. Traditional knots form the case where 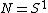 and
and 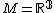 or
or 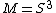 .
.The Schoenflies theorem states that the circle does not knot in the 2-sphere -- every circle in the 2-sphere is isotopic to the standard circle. Alexander's theorem states that the 2-sphere does not smoothly (or PL or tame topologically) knot in the 3-sphere. In the tame topological category, it's known that the
 -sphere does not knot in the
-sphere does not knot in the  -sphere for all
-sphere for all  . This is a theorem of Brown and Mazur. The Alexander horned sphere
. This is a theorem of Brown and Mazur. The Alexander horned sphereAlexander horned sphere
The Alexander horned sphere is a wild embedding of a sphere into space, discovered by . It is the particular embedding of a sphere in 3-dimensional Euclidean space obtained by the following construction, starting with a standard torus:...
is an example of a knotted 2-sphere in the 3-sphere which is not tame. In the smooth category, the
 -sphere is known not to knot in the
-sphere is known not to knot in the 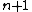 -sphere provided
-sphere provided 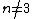 . The case
. The case  is a long-outstanding problem closely related to the question: does the 4-ball admit an exotic smooth structure
is a long-outstanding problem closely related to the question: does the 4-ball admit an exotic smooth structureExotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
?
Haefliger
André Haefliger
André Haefliger is a Swiss mathematician who works primarily on topology.He studied mathematics in Lausanne. He received his PhD in 1958 from the University of Strasbourg under the supervision of Charles Ehresmann with "Structures feuilletées et cohomologie à valeurs dans un faisceau de...
proved that there are no smooth j-dimensional knots in
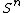 provided
provided 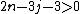 , and gave further examples of knotted spheres for all
, and gave further examples of knotted spheres for all 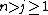 such that
such that 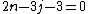 .
. 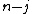 is called the codimension
is called the codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
of the knot. An interesting aspect of Haefliger's work is that the isotopy classes of embeddings of
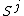 in
in 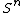 form a group, with group operation given by the connect sum, provided the co-dimension is greater than two.
form a group, with group operation given by the connect sum, provided the co-dimension is greater than two.Haefliger based his work on Smale's h-cobordism theorem. One of Smale's theorems is that when one deals with knots in co-dimension greater than two, even inequivalent knots have diffeomorphic complements. This gives the subject a different flavour than co-dimension 2 knot theory. If one allows topological or PL-isotopies, Zeeman proved that spheres do not knot when the co-dimension is larger than two. See a generalization to manifolds.
See also
- Knot theoryKnot theoryIn topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
- List of mathematical knots and links
- Pretzel linkPretzel linkIn knot theory, a branch of mathematics, a pretzel link is a special kind of link. A pretzel link which is also a knot is a pretzel knot....
knot - Prime knotPrime knotIn knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
- Rosette (design)Rosette (design)A rosette is a round, stylized flower design, used extensively in sculptural objects from antiquity. Appearing in Mesopotamia and used to decorate the funeral stele in Ancient Greece...
Further reading
- David W. Farmer & Theodore B. Stanford, Knots and Surfaces: A Guide to Discovering Mathematics, 1995.
- Colin C. Adams, The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, W. H. Freeman & Company, March 1994.
- Charles Livingstone, Knot Theory, The Mathematical Association of America, September 1996.

