
Borromean rings
Encyclopedia
In mathematics
, the Borromean rings consist of three topological circle
s which are link
ed and form a Brunnian link
, i.e., removing any ring results in two unlinked rings.
It is, however, true that one can use ellipses (third picture). These may be taken to be of arbitrarily small eccentricity
, i.e. no matter how close to being circular their shape may be, as long as they are not perfectly circular, they can form Borromean links if suitably positioned: for example, Borromean rings made from thin circles of elastic metal wire will bend.
Simplest is that the fundamental group
of the complement of two unlinked circles is the free group
on two generators, a and b, by the Seifert–van Kampen theorem
, and then the third loop has the class of the commutator
, [a, b] = aba−1b−1, as one can see from the link diagram: over one, over the next, back under the first, back under the second. This is non-trivial in the fundamental group, and thus the Borromean rings are linked.
Another way is that the cohomology
of the complement supports a non-trivial Massey product
, which is not the case for the unlink. This is a simple example of the Massey product and further, the algebra corresponds to the geometry: a 3-fold Massey product is a 3-fold product which is only defined if all the 2-fold products vanish, which corresponds to the Borromean rings being pairwise unlinked (2-fold products vanish), but linked overall (3-fold product does not vanish).
: the complement of the Borromean rings in the 3-sphere admits a complete hyperbolic
metric of finite volume. The canonical (Epstein-Penner) polyhedral decomposition of the complement consists of two ideal octahedra
.
 If one cuts the Borromean rings, one obtains one iteration of the standard braid; conversely, if one ties together the ends of (one iteration of) a standard braid, one obtains the Borromean rings. Just as removing one Borromean ring unlinks the remaining two, removing one strand of the standard braid unbraids the other two: they are the basic Brunnian link
If one cuts the Borromean rings, one obtains one iteration of the standard braid; conversely, if one ties together the ends of (one iteration of) a standard braid, one obtains the Borromean rings. Just as removing one Borromean ring unlinks the remaining two, removing one strand of the standard braid unbraids the other two: they are the basic Brunnian link
and Brunnian braid, respectively.
In the standard link diagram, the Borromean rings are ordered non-transitively, in a rock-paper-scissors
order. Using the colors above, these are red over yellow, yellow over blue, blue over red – and thus after removing any one ring, for the remaining two, one is above the other and they can be unlinked. Similarly, in the standard braid, each strand is above one of the others and below the other.
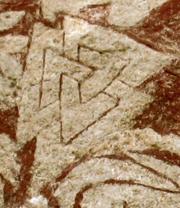

.svg.png) The name "Borromean rings" comes from their use in the coat of arms
The name "Borromean rings" comes from their use in the coat of arms
of the aristocratic
Borromeo
family in Italy
. The link itself is much older and has appeared in Gandhara (Afghan) Buddhist art from around the 2nd century, and in the form of the valknut
on Norse
image stones dating back to the 7th century.
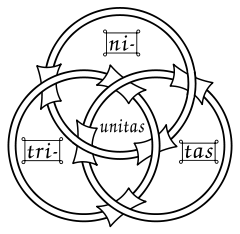
The Borromean rings have been used in different contexts to indicate strength in unity, e.g., in religion or art. In particular, some have used the design to symbolize the Trinity
. The psychoanalyst Jacques Lacan
famously found inspiration in the Borromean rings as a model for his topology of human subjectivity, with each ring representing a fundamental Lacanian component of reality (the "real", the "imaginary", and the "symbolic").
The Borromean rings were formerly used as the logo of the German Krupp
industrial concern and are used as part of the logo for the successor ThyssenKrupp
. The rings were used as the logo of Ballantine beer and are still used by the Ballantine brand beer, now produced by successor Falstaff
.
In 2006, the International Mathematical Union
decided at the 25th International Congress of Mathematicians in Madrid
, Spain
to use a new logo based on the Borromean rings.
A stone pillar at Marundeeswarar Temple
in Thiruvanmiyur
, Chennai, Tamil Nadu, India, has such a figure dating to before 6th century.
horns and the Diana of Poitiers crescents. An example with three distinct elements is the logo of Sport Club Internacional
.
Similarly, a monkey's fist
knot is essentially a 3-dimensional representation of the Borromean rings, albeit with three layers, in most cases.
, based on a depiction in the Principia Discordia
.
are the molecular counterparts of Borromean rings, which are mechanically-interlocked molecular architectures
.
In 1997, biologist
s Chengde Mao and coworkers of New York University
succeeded in constructing molecular Borromean rings
from DNA
(Nature
, volume 386, page 137, March 1997).
In 2003, chemist
Fraser Stoddart
and coworkers at UCLA utilised coordination chemistry to construct molecular Borromean rings
in one step from 18 components. This work was published in Science
2004, 304, 1308–1312. Abstract
, was predicted by physicist Vitaly Efimov
in 1970. A team of physicists led by Randall Hulet of Rice University
in Houston achieved this with a set of three bound lithium
atoms and published their findings in the online journal Science Express. In 2010, a team led by K. Tanaka created an Efimov state within a nucleus.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Borromean rings consist of three topological circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s which are link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
ed and form a Brunnian link
Brunnian link
In knot theory, a branch of mathematics, a Brunnian link is a nontrivial link that becomes trivial if any component is removed. In other words, cutting any loop frees all the other loops ....
, i.e., removing any ring results in two unlinked rings.
Mathematical properties
Although the typical picture of the Borromean rings (above right picture) may lead one to think the link can be formed from geometrically round circles, they cannot be. proves why a certain class of links including the Borromean links cannot be exactly circular. Alternatively, this can be seen from considering the link diagram: if one assumes that circles 1 and 2 touch at their two crossing points, then they either lie in a plane or a sphere. In either case, the third circle must pass through this plane or sphere four times, without lying in it, which is impossible; see .It is, however, true that one can use ellipses (third picture). These may be taken to be of arbitrarily small eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
, i.e. no matter how close to being circular their shape may be, as long as they are not perfectly circular, they can form Borromean links if suitably positioned: for example, Borromean rings made from thin circles of elastic metal wire will bend.
Linking
There are a number of ways of seeing that the Borromean rings cannot be unlinked.Simplest is that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the complement of two unlinked circles is the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on two generators, a and b, by the Seifert–van Kampen theorem
Seifert–van Kampen theorem
In mathematics, the Seifert-van Kampen theorem of algebraic topology, sometimes just called van Kampen's theorem, expresses the structure of the fundamental group of a topological space X, in terms of the fundamental groups of two open, path-connected subspaces U and V that cover X...
, and then the third loop has the class of the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
, [a, b] = aba−1b−1, as one can see from the link diagram: over one, over the next, back under the first, back under the second. This is non-trivial in the fundamental group, and thus the Borromean rings are linked.
Another way is that the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of the complement supports a non-trivial Massey product
Massey product
In algebraic topology, the Massey product is a cohomology operation of higher order introduced in , which generalizes the cup product.-Massey triple product:...
, which is not the case for the unlink. This is a simple example of the Massey product and further, the algebra corresponds to the geometry: a 3-fold Massey product is a 3-fold product which is only defined if all the 2-fold products vanish, which corresponds to the Borromean rings being pairwise unlinked (2-fold products vanish), but linked overall (3-fold product does not vanish).
Hyperbolic
The Borromean rings are a hyperbolic linkHyperbolic link
In mathematics, a hyperbolic link is a link in the 3-sphere with complement that has a complete Riemannian metric of constant negative curvature, i.e. has a hyperbolic geometry...
: the complement of the Borromean rings in the 3-sphere admits a complete hyperbolic
Hyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
metric of finite volume. The canonical (Epstein-Penner) polyhedral decomposition of the complement consists of two ideal octahedra
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
.
Connection to braid

Brunnian link
In knot theory, a branch of mathematics, a Brunnian link is a nontrivial link that becomes trivial if any component is removed. In other words, cutting any loop frees all the other loops ....
and Brunnian braid, respectively.
In the standard link diagram, the Borromean rings are ordered non-transitively, in a rock-paper-scissors
Rock-paper-scissors
Rock-paper-scissors is a hand game played by two people. The game is also known as roshambo, or another ordering of the three items ....
order. Using the colors above, these are red over yellow, yellow over blue, blue over red – and thus after removing any one ring, for the remaining two, one is above the other and they can be unlinked. Similarly, in the standard braid, each strand is above one of the others and below the other.
History of origin and depictions
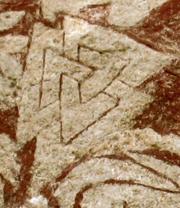


.svg.png)
Coat of arms
A coat of arms is a unique heraldic design on a shield or escutcheon or on a surcoat or tabard used to cover and protect armour and to identify the wearer. Thus the term is often stated as "coat-armour", because it was anciently displayed on the front of a coat of cloth...
of the aristocratic
Aristocracy
Aristocracy , is a form of government in which a few elite citizens rule. The term derives from the Greek aristokratia, meaning "rule of the best". In origin in Ancient Greece, it was conceived of as rule by the best qualified citizens, and contrasted with monarchy...
Borromeo
House of Borromeo
The aristocratic Borromeo family, said to date from before the twelfth century, were counts of Arona from the mid-fifteenth century and played important roles in the politics of the Duchy of Milan and in the Catholic Reformation...
family in Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
. The link itself is much older and has appeared in Gandhara (Afghan) Buddhist art from around the 2nd century, and in the form of the valknut
Valknut
The Valknut is a symbol consisting of three interlocked triangles, and appears on various Germanic objects. A number of theories have been proposed for its significance....
on Norse
Norsemen
Norsemen is used to refer to the group of people as a whole who spoke what is now called the Old Norse language belonging to the North Germanic branch of Indo-European languages, especially Norwegian, Icelandic, Faroese, Swedish and Danish in their earlier forms.The meaning of Norseman was "people...
image stones dating back to the 7th century.
The Borromean rings have been used in different contexts to indicate strength in unity, e.g., in religion or art. In particular, some have used the design to symbolize the Trinity
Trinity
The Christian doctrine of the Trinity defines God as three divine persons : the Father, the Son , and the Holy Spirit. The three persons are distinct yet coexist in unity, and are co-equal, co-eternal and consubstantial . Put another way, the three persons of the Trinity are of one being...
. The psychoanalyst Jacques Lacan
Jacques Lacan
Jacques Marie Émile Lacan was a French psychoanalyst and psychiatrist who made prominent contributions to psychoanalysis and philosophy, and has been called "the most controversial psycho-analyst since Freud". Giving yearly seminars in Paris from 1953 to 1981, Lacan influenced France's...
famously found inspiration in the Borromean rings as a model for his topology of human subjectivity, with each ring representing a fundamental Lacanian component of reality (the "real", the "imaginary", and the "symbolic").
The Borromean rings were formerly used as the logo of the German Krupp
Krupp
The Krupp family , a prominent 400-year-old German dynasty from Essen, have become famous for their steel production and for their manufacture of ammunition and armaments. The family business, known as Friedrich Krupp AG Hoesch-Krupp, was the largest company in Europe at the beginning of the 20th...
industrial concern and are used as part of the logo for the successor ThyssenKrupp
ThyssenKrupp
ThyssenKrupp AG is a German multinational conglomerate corporation headquartered in Duisburg Essen, Germany. The corporation consists of 670 companies worldwide. While ThyssenKrupp is one of the world's largest steel producers, the company also provides components and systems for the automotive...
. The rings were used as the logo of Ballantine beer and are still used by the Ballantine brand beer, now produced by successor Falstaff
Falstaff Brewing Corporation
The Falstaff Brewing Corporation was a major American brewery located in St. Louis, Missouri. With roots in the 1838 Lemp Brewery of St. Louis, the company was renamed after the Shakespearean character of Sir John Falstaff in 1903. Production peaked in 1965 with 7,010,218 barrels brewed, and then...
.
In 2006, the International Mathematical Union
International Mathematical Union
The International Mathematical Union is an international non-governmental organisation devoted to international cooperation in the field of mathematics across the world. It is a member of the International Council for Science and supports the International Congress of Mathematicians...
decided at the 25th International Congress of Mathematicians in Madrid
Madrid
Madrid is the capital and largest city of Spain. The population of the city is roughly 3.3 million and the entire population of the Madrid metropolitan area is calculated to be 6.271 million. It is the third largest city in the European Union, after London and Berlin, and its metropolitan...
, Spain
Spain
Spain , officially the Kingdom of Spain languages]] under the European Charter for Regional or Minority Languages. In each of these, Spain's official name is as follows:;;;;;;), is a country and member state of the European Union located in southwestern Europe on the Iberian Peninsula...
to use a new logo based on the Borromean rings.
A stone pillar at Marundeeswarar Temple
Marundeeswarar Temple
Marundeeswarar Temple is a legendary temple located in the breezy area of Thiruvanmiyur, Chennai adjacent to the beach of Bay of Bengal. This is the biggest temple in Thiruvanmiyur. This is a magnificent temple built for Lord Shiva, in his incarnation of Lord Marundeeswarar. Lord Marundeeswarar is...
in Thiruvanmiyur
Thiruvanmiyur
-Transport:The area is easily accessible by Metropolitan Transport Corporation buses and has a sprawling bus terminus. Bus Routes connecting Thiruvanmiyur with other places in Chennai are: 1, 1A, 1C, 1D, 6D, 22A, 23C Extn., 29M,29C Extn., 41C, A47, 47A, 47D, M1, M49, M7, C51, T51, M23, M19, M70,...
, Chennai, Tamil Nadu, India, has such a figure dating to before 6th century.
Partial Borromean rings
In medieval and renaissance Europe, a number of visual signs are found that consist of three elements interlaced together in the same way that the Borromean rings are shown interlaced (in their conventional two-dimensional depiction), but the individual elements are not closed loops. Examples of such symbols are the Snoldelev stoneSnoldelev Stone
The Snoldelev Stone, listed as DR 248 in the Rundata catalog, is a 9th century runestone that was originally located at Snoldelev, Ramsø, Denmark.-Description:...
horns and the Diana of Poitiers crescents. An example with three distinct elements is the logo of Sport Club Internacional
Sport Club Internacional
Sport Club Internacional is a Brazilian football team and multi-sport club from Porto Alegre, Rio Grande do Sul, founded on April 4, 1909, and are one of the only five clubs to have never been relegated, along with Santos, São Paulo, Flamengo and Cruzeiro. They play in red shirts, white shorts and...
.
Similarly, a monkey's fist
Monkey's fist
A monkey's fist or monkey paw is a type of knot, so named because it looks somewhat like a small bunched fist/paw. It is tied at the end of a rope to serve as a weight, making it easier to throw, and also as an ornamental knot. This type of weighted rope can be used as an improvised weapon,...
knot is essentially a 3-dimensional representation of the Borromean rings, albeit with three layers, in most cases.
Balancing knives
Using the pattern in the incomplete Borromean rings, one can balance three knives on three supports, such as three bottles or glasses, providing a support in the middle for a fourth bottle or glass.Multiple Borromean rings
Some knot-theoretic links contain multiple Borromean rings configurations; one five-loop link of this type is used as a symbol in DiscordianismDiscordianism
Discordianism is a religion based on the worship of Eris , the Greco-Roman goddess of strife. It was founded circa 1958–1959 after the publication of its holy book the Principia Discordia, written by Malaclypse the Younger and Omar Khayyam Ravenhurst after a series of shared hallucinations at a...
, based on a depiction in the Principia Discordia
Principia Discordia
Principia Discordia is a Discordian religious text written by Greg Hill and Kerry Thornley . It was originally published under the title "Principia Discordia or How The West Was Lost" in a limited edition of 5 copies in 1965...
.
Molecular Borromean rings
Molecular Borromean ringsMolecular Borromean rings
Molecular Borromean rings are an example of a mechanically-interlocked molecular architecture in which three macrocycles are interlocked in such a way that breaking any macrocycle allows the others to disassociate. They are the smallest examples of Borromean rings. The synthesis of molecular...
are the molecular counterparts of Borromean rings, which are mechanically-interlocked molecular architectures
Mechanically-interlocked molecular architectures
Mechanically interlocked molecular architectures are connections of molecules not through traditional bonds, but instead as a consequence of their topology. This connection of molecules is analogous to keys on a key chain loop. The keys are not directly connected to the key chain loop but they...
.
In 1997, biologist
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
s Chengde Mao and coworkers of New York University
New York University
New York University is a private, nonsectarian research university based in New York City. NYU's main campus is situated in the Greenwich Village section of Manhattan...
succeeded in constructing molecular Borromean rings
Molecular Borromean rings
Molecular Borromean rings are an example of a mechanically-interlocked molecular architecture in which three macrocycles are interlocked in such a way that breaking any macrocycle allows the others to disassociate. They are the smallest examples of Borromean rings. The synthesis of molecular...
from DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
(Nature
Nature (journal)
Nature, first published on 4 November 1869, is ranked the world's most cited interdisciplinary scientific journal by the Science Edition of the 2010 Journal Citation Reports...
, volume 386, page 137, March 1997).
In 2003, chemist
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
Fraser Stoddart
James Fraser Stoddart
Sir James Fraser Stoddart is a Scottish chemist currently at the Department of Chemistry at Northwestern University. He works in the area of supramolecular chemistry and nanotechnology...
and coworkers at UCLA utilised coordination chemistry to construct molecular Borromean rings
Molecular Borromean rings
Molecular Borromean rings are an example of a mechanically-interlocked molecular architecture in which three macrocycles are interlocked in such a way that breaking any macrocycle allows the others to disassociate. They are the smallest examples of Borromean rings. The synthesis of molecular...
in one step from 18 components. This work was published in Science
Science (journal)
Science is the academic journal of the American Association for the Advancement of Science and is one of the world's top scientific journals....
2004, 304, 1308–1312. Abstract
Quantum-mechanical rings
A quantum-mechanical analog of Borromean rings, called an Efimov stateEfimov state
The Efimov effect is an effect in the quantum mechanics of Few-body systems predicted by the Soviet theoretical physicist V. N. Efimov in 1970. Efimov’s effect refers to a scenario in which three identical bosons interact, with the prediction of an infinite series of excited three-body energy...
, was predicted by physicist Vitaly Efimov
Vitaly Efimov
Vitaly N. Efimov is a Russian theoretical physicist. He proposed the existence of a novel and exotic state of matter now dubbed the Efimov State as a researcher in A.F...
in 1970. A team of physicists led by Randall Hulet of Rice University
Rice University
William Marsh Rice University, commonly referred to as Rice University or Rice, is a private research university located on a heavily wooded campus in Houston, Texas, United States...
in Houston achieved this with a set of three bound lithium
Lithium
Lithium is a soft, silver-white metal that belongs to the alkali metal group of chemical elements. It is represented by the symbol Li, and it has the atomic number 3. Under standard conditions it is the lightest metal and the least dense solid element. Like all alkali metals, lithium is highly...
atoms and published their findings in the online journal Science Express. In 2010, a team led by K. Tanaka created an Efimov state within a nucleus.
See also
- Knot theoryKnot theoryIn topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
- Link (knot theory)Link (knot theory)In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
- Venn diagramVenn diagramVenn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
- GankyilGankyilThe Gankyil[Tibetan:དགའ་འཁྱིལ་] is a symbol and ritual tool in Tibetan Buddhism, Bön, Himalayan Shamanism and Korean Buddhism. In Bön and Nyingma Dzogchen lineages, the Gankyil is the principal symbol and teaching tool: it is symbolic of primordial energy and represents the central unity and...
- ValknutValknutThe Valknut is a symbol consisting of three interlocked triangles, and appears on various Germanic objects. A number of theories have been proposed for its significance....
External links
- Site devoted to the Borromean Rings.
- The Borromean link and related entities in knot theory
- The Borromean Rings at the wiki Knot Atlas.
- History of the Borromean rings
- Borromean rings and John Robinson (sculptor)John Robinson (sculptor)John Robinson was a British sculptor and co-founder of the . Accounts of his work may be seen at the , the website of the and the June and July 2007, issues of...
. - African Borromean ring carving
- Borromean rings spinning as a group
- Video animation: International Mathematical Union logo

