
Cinquefoil knot
Encyclopedia
In knot theory
, the cinquefoil knot, also known as Solomon's seal knot or the pentafoil knot, is one of two knots with crossing number
five, the other being the three-twist knot
. It is listed as the 51 knot in the Alexander-Briggs notation, and can also be described as the (5,2)-torus knot
. The cinquefoil is the closed version of the double overhand knot.
The cinquefoil is a prime knot
. Its writhe
is 5, and it is invertible
but not amphichiral
. Its Alexander polynomial
is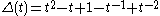 ,
,
its Conway polynomial
is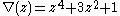 ,
,
and its Jones polynomial is
Surprisingly, these are the same as the Alexander, Conway, and Jones polynomials of the knot 10132. However, the Kauffman polynomial can be used to distinguish between these two knots.
The name “cinquefoil” comes from the five-petaled flowers of plants in the genus Potentilla
.
Students can be introduced to the essentials of knot theory by being challenged to create edible cinquefoil pretzels.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the cinquefoil knot, also known as Solomon's seal knot or the pentafoil knot, is one of two knots with crossing number
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
five, the other being the three-twist knot
Three-twist knot
In knot theory, the three-twist knot is the twist knot with three-half twists. It is listed as the 52 knot in the Alexander-Briggs notation, and is one of two knots with crossing number five, the other being the cinquefoil knot....
. It is listed as the 51 knot in the Alexander-Briggs notation, and can also be described as the (5,2)-torus knot
Torus knot
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
. The cinquefoil is the closed version of the double overhand knot.
The cinquefoil is a prime knot
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
. Its writhe
Writhe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
is 5, and it is invertible
Invertible knot
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant...
but not amphichiral
Amphichiral knot
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot or amphicheiral knot. The chirality of a knot is a knot invariant...
. Its Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
is
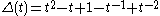 ,
,its Conway polynomial
Conway polynomial
In mathematics, Conway polynomial can refer to:* the Alexander–Conway polynomial in knot theory* the Conway polynomial...
is
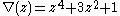 ,
,and its Jones polynomial is

Surprisingly, these are the same as the Alexander, Conway, and Jones polynomials of the knot 10132. However, the Kauffman polynomial can be used to distinguish between these two knots.
The name “cinquefoil” comes from the five-petaled flowers of plants in the genus Potentilla
Potentilla
Potentilla is the genus of typical cinquefoils, containing about 500 species of annual, biennial and perennial herbs in the rose family Rosaceae. They are generally Holarctic in distribution, though some may even be found in montane biomes of the New Guinea Highlands...
.
Students can be introduced to the essentials of knot theory by being challenged to create edible cinquefoil pretzels.

