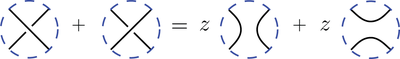Kauffman polynomial
Encyclopedia
In knot theory
, the Kauffman polynomial is a 2-variable knot polynomial
due to Louis Kauffman
. It is initially defined on a link
diagram as
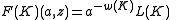
where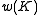
is the writhe
of the link diagram and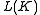
is a polynomial in a and z defined on link diagrams by the following properties:
Here
is a strand and 
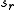(resp. 
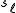) is the same strand with a right-handed (resp. left-handed) curl added (using a type I Reidemeister move).
Additionally L must satisfy Kauffman's skein relation
:
The pictures represent the L polynomial of the diagrams which differ inside a disc as shown but are identical outside.
Kauffman showed that L exists and is a regular isotopy
invariant of unoriented links. It follows easily that F is an ambient isotopy
invariant of oriented links.
The Jones polynomial is a special case of the Kauffman polynomial, as the L polynomial specializes to the bracket polynomial
. The Kauffman polynomial is related to Chern-Simons gauge theories for SO(N) in the same way that the HOMFLY polynomial
is related to Chern-Simons gauge theories for SU(N) (see Witten's article
"Quantum field theory and the Jones polynomial", in Commun. Math. Phys.)
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the Kauffman polynomial is a 2-variable knot polynomial
Knot polynomial
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.-History:The first knot polynomial, the Alexander polynomial, was introduced by J. W...
due to Louis Kauffman
Louis Kauffman
Louis H. Kauffman is an American mathematician, topologist, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago...
. It is initially defined on a link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
diagram as
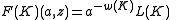
where
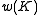is the writheWrithe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
of the link diagram and
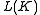is a polynomial in a and z defined on link diagrams by the following properties:
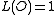(O is the unknot)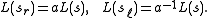
- L is unchanged under type II and III Reidemeister moveReidemeister moveIn the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
s
Here
is a strand and 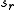(resp. 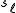) is the same strand with a right-handed (resp. left-handed) curl added (using a type I Reidemeister move).Additionally L must satisfy Kauffman's skein relation
Skein relation
A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial which is an invariant of the knot. If two diagrams have different polynomials, they represent different knots. The reverse may not...
:
The pictures represent the L polynomial of the diagrams which differ inside a disc as shown but are identical outside.
Kauffman showed that L exists and is a regular isotopy
Regular isotopy
In the mathematical subject of knot theory, a regular isotopy of a link diagram is the equivalence relation generated by using the 2nd and 3rd Reidemeister moves only. The notion of regular isotopy was introduced by Louis Kauffman . It can be thought of as an isotopy of a ribbon pressed flat...
invariant of unoriented links. It follows easily that F is an ambient isotopy
Ambient isotopy
In the mathematical subject of topology, an ambient isotopy, also called an h-isotopy, is a kind of continuous distortion of an "ambient space", a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the...
invariant of oriented links.
The Jones polynomial is a special case of the Kauffman polynomial, as the L polynomial specializes to the bracket polynomial
Bracket polynomial
In the mathematical field of knot theory, the bracket polynomial is a polynomial invariant of framed links. Although it is not an invariant of knots or links , a suitably "normalized" version yields the famous knot invariant called the Jones polynomial...
. The Kauffman polynomial is related to Chern-Simons gauge theories for SO(N) in the same way that the HOMFLY polynomial
HOMFLY polynomial
In the mathematical field of knot theory, the HOMFLY polynomial, sometimes called the HOMFLY-PT polynomial or the generalized Jones polynomial, is a 2-variable knot polynomial, i.e. a knot invariant in the form of a polynomial of variables m and l....
is related to Chern-Simons gauge theories for SU(N) (see Witten's article
"Quantum field theory and the Jones polynomial", in Commun. Math. Phys.)