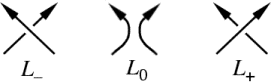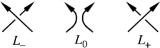
Skein relation
Encyclopedia
A central question in the mathematical theory of knots
is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial
which is an invariant of the knot
. If two diagrams have different polynomial
s, they represent different knots. The reverse may not be true.
Skein relations are often used to give a simple definition of knot polynomials. Informally, a skein relation gives a linear relation between the values of a knot polynomial on a collection of three links
which differ from each other only in a small region. For some knot polynomials, such as the Conway
, Alexander
, and Jones polynomials, the relevant skein relations are sufficient to calculate the polynomial recursively
. For others, such as the HOMFLYPT polynomial, more complicated algorithms are necessary.
The three diagrams are labelled as follows. Turn the diagrams so the directions at the crossing in question are both roughly northward. One diagram will have northwest over northeast, it is labelled L−. Another will have northeast over northwest, it's L+. The remaining diagram is lacking that crossing and is labelled L0.
(The labelling is actually independent of direction insofar as it remains the same if all directions are reversed. Thus polynomials on undirected knots are unambiguously defined by this method. However, the directions on links are a vital detail to retain as one recurses through a polynomial calculation.)
It is also sensible to think in a generative sense, by taking an existing link diagram and "patching" it to make the other two—just so long as the patches are applied with compatible directions.
To recursively define a knot (link) polynomial, a function F is fixed and for any triple of diagrams and their polynomials labelled as above,
or more pedantically
for all 
(Finding an F which produces polynomials independent of the sequences of crossings used in a recursion is no trivial exercise.)
More formally, a skein relation can be thought of as defining the kernel
of a quotient map from the planar algebra
of tangles. Such a map corresponds to a knot polynomial if all closed diagrams are taken to some (polynomial) multiple of the image of the empty diagram.
showed how to compute the Alexander polynomial using skein relations. As it is recursive
, it is not quite so direct as Alexander's original matrix
method; on the other hand, parts of the work done for one knot will apply to others. In particular, the network of diagrams is the same for all skein-related polynomials.
Let function P from link diagrams to Laurent series
in
be
such that
and a triple of skein-relation diagrams 
satisfies the equation
Then P maps a knot to one of its Alexander polynomials.
In this example, we calculate the Alexander polynomial of the cinquefoil knot
(
), the alternating knot
with five crossings in its minimal diagram. At each stage we exhibit a relationship involving a more complex link and two simpler diagrams. Note that the more complex link is on the right in each step below except the last. For convenience, let A = x−1/2−x1/2.
To begin, we create two new diagrams by patching one of the cinquefoil's crossings (highlighted in yellow) so
The first diagram is actually a trefoil; the second diagram is two unknots with four crossings. Patching the latter
gives, again, a trefoil, and two unknots with two crossings (the Hopf link
http://mathworld.wolfram.com/HopfLink.html). Patching the trefoil
gives the unknot and, again, the Hopf link. Patching the Hopf link
gives a link with 0 crossings (unlink) and an unknot. The unlink takes a bit of sneakiness:
We now have enough relations to compute the polynomials of all the links we've encountered, and can use the above equations in reverse order to work up to the cinquefoil knot itself:
Thus the Alexander polynomial for a cinquefoil is P(x) = x−2 -x -1 +1 -x +x2.
Useful formulas:
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial
Knot polynomial
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.-History:The first knot polynomial, the Alexander polynomial, was introduced by J. W...
which is an invariant of the knot
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
. If two diagrams have different polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, they represent different knots. The reverse may not be true.
Skein relations are often used to give a simple definition of knot polynomials. Informally, a skein relation gives a linear relation between the values of a knot polynomial on a collection of three links
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
which differ from each other only in a small region. For some knot polynomials, such as the Conway
Conway polynomial
In mathematics, Conway polynomial can refer to:* the Alexander–Conway polynomial in knot theory* the Conway polynomial...
, Alexander
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
, and Jones polynomials, the relevant skein relations are sufficient to calculate the polynomial recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. For others, such as the HOMFLYPT polynomial, more complicated algorithms are necessary.
Definition
A skein relationship requires three link diagrams that are identical except at one crossing. The three diagrams must exhibit the three possibilities that could occur at that crossing, it could be under, it could be over or it could not exist at all. Link diagrams must be considered because a single skein change can alter a diagram from representing a knot to representing a link and vice versa. Depending on the knot polynomial in question, the links (or tangles) appearing in a skein relation may be oriented or unoriented.The three diagrams are labelled as follows. Turn the diagrams so the directions at the crossing in question are both roughly northward. One diagram will have northwest over northeast, it is labelled L−. Another will have northeast over northwest, it's L+. The remaining diagram is lacking that crossing and is labelled L0.
(The labelling is actually independent of direction insofar as it remains the same if all directions are reversed. Thus polynomials on undirected knots are unambiguously defined by this method. However, the directions on links are a vital detail to retain as one recurses through a polynomial calculation.)
It is also sensible to think in a generative sense, by taking an existing link diagram and "patching" it to make the other two—just so long as the patches are applied with compatible directions.
To recursively define a knot (link) polynomial, a function F is fixed and for any triple of diagrams and their polynomials labelled as above,
or more pedantically
for all (Finding an F which produces polynomials independent of the sequences of crossings used in a recursion is no trivial exercise.)
More formally, a skein relation can be thought of as defining the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of a quotient map from the planar algebra
Planar algebra
In mathematics, planar algebras first appeared in the work of Vaughan Jones on the standard invariant of a II1 subfactor . They also provide an appropriate algebraic framework for many knot invariants , and have been used in describing the properties of Khovanov homology with respect to tangle...
of tangles. Such a map corresponds to a knot polynomial if all closed diagrams are taken to some (polynomial) multiple of the image of the empty diagram.
Example
Sometime in the early 1960s, ConwayJohn Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
showed how to compute the Alexander polynomial using skein relations. As it is recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
, it is not quite so direct as Alexander's original matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
method; on the other hand, parts of the work done for one knot will apply to others. In particular, the network of diagrams is the same for all skein-related polynomials.
Let function P from link diagrams to Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
in
besuch that
and a triple of skein-relation diagrams satisfies the equationThen P maps a knot to one of its Alexander polynomials.
In this example, we calculate the Alexander polynomial of the cinquefoil knot
Cinquefoil knot
In knot theory, the cinquefoil knot, also known as Solomon's seal knot or the pentafoil knot, is one of two knots with crossing number five, the other being the three-twist knot. It is listed as the 51 knot in the Alexander-Briggs notation, and can also be described as the -torus knot...
(
), the alternating knotAlternating knot
In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
with five crossings in its minimal diagram. At each stage we exhibit a relationship involving a more complex link and two simpler diagrams. Note that the more complex link is on the right in each step below except the last. For convenience, let A = x−1/2−x1/2.
To begin, we create two new diagrams by patching one of the cinquefoil's crossings (highlighted in yellow) so
- P(
) = A × P(
) + P()
The first diagram is actually a trefoil; the second diagram is two unknots with four crossings. Patching the latter
- P(
) = A × P(
) + P(
)
gives, again, a trefoil, and two unknots with two crossings (the Hopf link
Hopf link
thumb|right|[[Skein relation]] for the Hopf link.In mathematical knot theory, the Hopf link, named after Heinz Hopf, is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly once...
http://mathworld.wolfram.com/HopfLink.html). Patching the trefoil
- P(
) = A × P(
) + P(
)
gives the unknot and, again, the Hopf link. Patching the Hopf link
- P(
) = A × P(
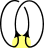) + P(
)
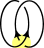gives a link with 0 crossings (unlink) and an unknot. The unlink takes a bit of sneakiness:
- P(
) = A × P(
) + P(
)
We now have enough relations to compute the polynomials of all the links we've encountered, and can use the above equations in reverse order to work up to the cinquefoil knot itself:
| knot name | diagrams | P (diagram) | ||
|---|---|---|---|---|
| skein equation | ? | P in full | ||
| unknot | 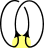| defined as 1 | x→1 | |
| unlink | | 1=A?+1 | 0 | x→0 |
| Hopf link | 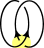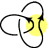| 0=A1+? | -A | x→x1/2-x-1/2 |
| trefoil | | 1=A(-A)+? | 1+A2 | x→x-1-1+x |
| 4 crossing link | | -A=A(1+A2)+? | -A(2+A2) | x→-x-3/2+x-1/2-x1/2+x3/2 |
| cinquefoil | | 1+A2=A(-A(2+A2))+? | 1+3A2+A4 | x→x-2-x-1+1-x+x2 |
Thus the Alexander polynomial for a cinquefoil is P(x) = x−2 -x -1 +1 -x +x2.
Useful formulas:
- A = (1 − x)/x1/2
- A2 = (1 − 2x + x2)/x
- A3 = (1 − x)3/x3/2 = (1 − 3x + 3x2 − x3)/x3/2
- A4 = (1 − x)4/x2 = (1 − 4x + 6x2 − 4x3 + x4)/x2