Alternating knot

Alternating Knot

	Email		Print
	Bookmark		Link

Alternating knot

In knot theory

Knot theory

In mathematics, knot theory is the area of topology that studies knot s. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs drastically in that the ends are joined together to prevent it from becoming undone....
, a link

Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations ....
diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram.

Many of the knots with crossing number less than 10 are alternating. This fact and useful properties of alternating knots, such as the Tait conjectures, was what enabled early knot tabulators, such as Tait, to construct tables with relatively few mistakes or omissions.

Discussion

Ask a question about 'Alternating knot'

Start a new discussion about 'Alternating knot'

Answer questions from other users

Full Discussion Forum

Encyclopedia

In knot theory

Knot theory

Knot (mathematics)

Prime knot

In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-unknot knot which cannot be written as the knot sum of two non-trivial knots....
s have 8 crossings

Crossing number

In mathematics, crossing numbers arise in two related contexts: in knot theory and in graph theory.*In knot theory, crossing number of a knot refers to the minimal number of crossings in any knot diagram for the knot....
(and there are three such).

It is conjectured that as the crossing number increases, the percentage of knots that are alternating goes to 0 exponentially quickly.

Alternating links end up having an important role in knot theory and 3-manifold theory, due to their complements having useful and interesting geometric and topological properties. This led Ralph Fox

Ralph Fox

Ralph Hartzler Fox was an United States of America mathematician. As a professor at Princeton University, he taught and advised many of the contributors to the Golden Age of differential topology, and he played an important role in the modernization and main-streaming of knot theory....
to ask, "What is an alternating knot?" By this he was asking what non-diagrammatic properties of the knot complement would characterize alternating knots.

Various geometric and topological information is revealed in an alternating diagram. Primeness

Prime knot

Split link

In the mathematics field of knot theory, a split link is a link that has a 2-sphere in its complement separating one or more link components from the others....
of a link is easily seen from the diagram. Applying Seifert's algorithm to a knot results in a minimal genus Seifert surface

Seifert surface

In mathematics, a Seifert surface is a surface whose boundary of a manifold is a given knot or link . Such surfaces can be used to study the properties of the associated knot or link....
. The crossing number

Crossing number

In mathematics, crossing numbers arise in two related contexts: in knot theory and in graph theory.*In knot theory, crossing number of a knot refers to the minimal number of crossings in any knot diagram for the knot....
of a reduced, alternating diagram is the crossing number of the knot. This last is one of the celebrated Tait Conjectures.

An alternating knot diagram is in one to one correspondence with a planar graph

Planar graph

In graph theory, a planar graph is a graph which can be graph embedding in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints....
. Each crossing is associated with an edge and half of the connected components of the complement of the diagram are associated with vertices in a checker board manner.

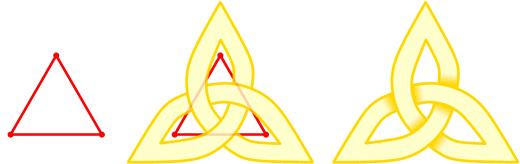
Tait conjectures

The Tait conjectures are:

Any reduced diagram of an alternating link has the fewest possible crossings
Crossing number

In mathematics, crossing numbers arise in two related contexts: in knot theory and in graph theory.*In knot theory, crossing number of a knot refers to the minimal number of crossings in any knot diagram for the knot....
.
Any two reduced diagrams of the same alternating knot
Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations ....
have the same writhe
Writhe

In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
.
Given any two reduced alternating diagrams D₁ and D₂ of an oriented, prime alternating link: D₁ may be transformed to D₂ by means of a sequence of certain simple moves called flype
Flype

In the knot theory, a flype is a knot move used in the Tait conjectures.It consists of twisting a part of a knot, a tangle : T by 180 degrees....
s. Also known as the Tait flyping conjecture.

Morwen Thistlethwaite

Morwen B. Thistlethwaite is a Knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory....
, Louis Kauffman

Louis Kauffman

Louis H. Kauffman is an American mathematician, topology, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago....
and K. Murasugi proved the first two Tait conjectures in 1987 and Morwen Thistlethwaite

Morwen Thistlethwaite

William Menasco

William W. Menasco is a topologist and a professor at the University at Buffalo. He is best known for his work in knot theory....
proved the Tait flyping conjecture in 1991.

Hyperbolic volume

Menasco

William Menasco

William W. Menasco is a topologist and a professor at the University at Buffalo. He is best known for his work in knot theory....
, applying Thurston

William Thurston

William Paul Thurston is an United States mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields medal for the depth and originality of his contributions to mathematics....
's geometrization theorem for Haken manifold

Haken manifold

In mathematics, a Haken manifold is a compact space, P?-irreducible 3-manifold that contains a 2-sided incompressible surface. Sometimes one considers only orientable Haken manifolds, in which case a Haken manifold is a compact, orientable, irreducible 3-manifold that contains an orientable, incompressible surface....
s, showed that any prime, non-split alternating link is hyperbolic

Hyperbolic link

In mathematics, a hyperbolic link is a link in the 3-sphere with knot complement that has a complete Riemannian metric of constant negative curvature, i.e....
, i.e. the link complement has a hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced. The parallel postulate in Euclidean geometry is equivalent to the statement that, in two dimensional space, for any given line l and point P not on l, there is exactly one line through P th...
, unless the link is a torus link.

Thus hyperbolic volume is an invariant of many alternating links. Marc Lackenby has shown that the volume has upper and lower linear bounds as functions of the number of twist regions of a reduced, alternating diagram.

External links

at MathWorld
MathWorld

MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by Wolfram Research Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana-Champaign....
at MathWorld
to build an alternating knot from its planar graph