Louis Kauffman
Encyclopedia
Louis H. Kauffman is an American mathematician
, topologist
, and professor of Mathematics
in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago
. He is known for the introduction and development of the bracket polynomial
and Kauffman polynomial.
in mathematics
from Princeton University
in 1972.
Kauffman has worked at many places as a visiting professor and researcher, including the University of Zaragoza in Spain, the University of Iowa in Iowa City, the Institute Hautes Etudes Scientifiques in Bures Sur Yevette, France, the Institute Henri Poincaré in Paris, France, the Università di Bologna, Italy, the Universidade Federal de Pernambuco in Recife, Brasil, and the Newton Institute in Cambridge England.
He is the founding editor and one of the managing editors of the Journal of Knot Theory and Its Ramifications
, and editor of the World Scientific Book Series On Knots and Everything. He writes a column entitled Virtual Logic for the journal Cybernetics and Human Knowing
From 2005 to 2008 he was president of the American Society for Cybernetics
. He is the 1993 recipient of the Warren McCulloch award of the American Society for Cybernetics and the 1996 award of the Alternative Natural Philosophy Association for his work in discrete physics. He plays
clarinet in the ChickenFat Klezmer Orchestra in Chicago.
and connections with statistical mechanics
, quantum theory
, algebra
, combinatorics
and foundations. In topology
he introduced and developed the bracket polynomial
and Kauffman polynomial.
, the bracket polynomial
, also known as the Kauffman bracket, is a polynomial
invariant of framed links. Although it is not an invariant of knots or links (as it is not invariant under type I Reidemeister move
s), a suitably "normalized" version yields the famous knot invariant
called the Jones polynomial. The bracket polynomial plays an important role in unifying the Jones polynomial with other quantum invariant
s. In particular, Kauffman's interpretation of the Jones polynomial allows generalization to state sum invariants of 3-manifold
s. Recently the bracket polynomial formed the basis for Mikhail Khovanov's construction of a homology for knots and links, creating
a stronger invariant than the Jones polynomial and such that the graded Euler chacteristic of the Khovanov homology
is equal to the original
Jones polynomial. The generators for the chain complex of the Khovanov homology are states of the bracket polynomial decorated with elements
of a Frobenius algebra
.
due to Louis Kauffman. It is defined as
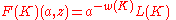
where
is the writhe
and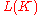
is a regular isotopy
invariant which generalizes the bracket polynomial.
Articles and papers, a selection:
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, topologist
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, and professor of Mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago
University of Illinois at Chicago
The University of Illinois at Chicago, or UIC, is a state-funded public research university located in Chicago, Illinois, United States. Its campus is in the Near West Side community area, near the Chicago Loop...
. He is known for the introduction and development of the bracket polynomial
Bracket polynomial
In the mathematical field of knot theory, the bracket polynomial is a polynomial invariant of framed links. Although it is not an invariant of knots or links , a suitably "normalized" version yields the famous knot invariant called the Jones polynomial...
and Kauffman polynomial.
Biography
Kauffman was valedictorian of his graduating class at Norwood Norfolk Central High School in 1962. He received his B.S. at MIT in 1966 and his Ph.D.Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
from Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
in 1972.
Kauffman has worked at many places as a visiting professor and researcher, including the University of Zaragoza in Spain, the University of Iowa in Iowa City, the Institute Hautes Etudes Scientifiques in Bures Sur Yevette, France, the Institute Henri Poincaré in Paris, France, the Università di Bologna, Italy, the Universidade Federal de Pernambuco in Recife, Brasil, and the Newton Institute in Cambridge England.
He is the founding editor and one of the managing editors of the Journal of Knot Theory and Its Ramifications
Journal of Knot Theory and Its Ramifications
The Journal of Knot Theory and Its Ramifications was established in 1992 by Louis Kauffman and was the first journal purely devoted to knot theory. It is an interdisciplinary journal covering developments in knot theory, with emphasis on creating connections between with other branches of...
, and editor of the World Scientific Book Series On Knots and Everything. He writes a column entitled Virtual Logic for the journal Cybernetics and Human Knowing
From 2005 to 2008 he was president of the American Society for Cybernetics
American Society for Cybernetics
The American Society for Cybernetics is an American non-profit scholastic organization for organization for the advancement of cybernetics as a science and the interdisciplinary collaboration and synthesis of cybernetics. The society contributes to the cooperation around the research and...
. He is the 1993 recipient of the Warren McCulloch award of the American Society for Cybernetics and the 1996 award of the Alternative Natural Philosophy Association for his work in discrete physics. He plays
clarinet in the ChickenFat Klezmer Orchestra in Chicago.
Work
Kauffman's research interests are in the fields of cybernetics, topology and foundations of mathematics and physics. His work is primarily in the topics of knot theoryKnot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
and connections with statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, quantum theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and foundations. In topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
he introduced and developed the bracket polynomial
Bracket polynomial
In the mathematical field of knot theory, the bracket polynomial is a polynomial invariant of framed links. Although it is not an invariant of knots or links , a suitably "normalized" version yields the famous knot invariant called the Jones polynomial...
and Kauffman polynomial.
Bracket polynomial
In the mathematical field of knot theoryKnot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the bracket polynomial
Bracket polynomial
In the mathematical field of knot theory, the bracket polynomial is a polynomial invariant of framed links. Although it is not an invariant of knots or links , a suitably "normalized" version yields the famous knot invariant called the Jones polynomial...
, also known as the Kauffman bracket, is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
invariant of framed links. Although it is not an invariant of knots or links (as it is not invariant under type I Reidemeister move
Reidemeister move
In the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
s), a suitably "normalized" version yields the famous knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
called the Jones polynomial. The bracket polynomial plays an important role in unifying the Jones polynomial with other quantum invariant
Quantum invariant
In the mathematical field of knot theory, a quantum invariant of a knot or link is a linear sum of colored Jones polynomial of surgery presentations of the knot complement.-List of invariants:*Finite type invariant*Kontsevich invariant*Kashaev's invariant...
s. In particular, Kauffman's interpretation of the Jones polynomial allows generalization to state sum invariants of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s. Recently the bracket polynomial formed the basis for Mikhail Khovanov's construction of a homology for knots and links, creating
a stronger invariant than the Jones polynomial and such that the graded Euler chacteristic of the Khovanov homology
Khovanov homology
In mathematics, Khovanov homology is an invariant of oriented knots and links that arises as the homology of a chain complex. It may be regarded as a categorification of the Jones polynomial....
is equal to the original
Jones polynomial. The generators for the chain complex of the Khovanov homology are states of the bracket polynomial decorated with elements
of a Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
.
Kauffman polynomial
The Kauffman polynomial is a 2-variable knot polynomialKnot polynomial
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.-History:The first knot polynomial, the Alexander polynomial, was introduced by J. W...
due to Louis Kauffman. It is defined as
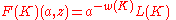
where
is the writheWrithe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
and
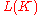is a regular isotopyRegular isotopy
In the mathematical subject of knot theory, a regular isotopy of a link diagram is the equivalence relation generated by using the 2nd and 3rd Reidemeister moves only. The notion of regular isotopy was introduced by Louis Kauffman . It can be thought of as an isotopy of a ribbon pressed flat...
invariant which generalizes the bracket polynomial.
Publications
Louis H. Kauffman is author of several monographs on knot theory and mathematical physics. His publication list numbers over 170. Books:- 1987, On Knots, Princeton University Press 498 pp.
- 1993, Quantum Topology (Series on Knots & Everything), with Randy A. Baadhio, World Scientific Pub Co Inc, 394 pp.
- 1994, Temperley-Lieb Recoupling Theory and Invariants of 3-Manifolds, with Sostenes Lins, Princeton University Press, 312 pp.
- 1995, Knots and Applications (Series on Knots and Everything, Vol 6)
- 1995, The Interface of Knots and Physics: American Mathematical Society Short Course January 2-3, 1995 San Francisco, California (Proceedings of Symposia in Applied Mathematics), with the American Mathematical Society.
- 1998, Knots at Hellas 98: Proceedings of the International Conference on Knot Theory and Its Ramifications, with Cameron McA. GordonCameron Gordon (mathematician)Cameron Gordon is a Professor and Sid W. Richardson Foundation Regents Chair in the Department of mathematics at the University of Texas at Austin, known for his work in knot theory. Among his notable results is his work with Marc Culler, John Luecke, and Peter Shalen on the cyclic surgery theorem...
, Vaughan F. R. Jones and Sofia Lambropoulou, - 1999, Ideal Knots, with Andrzej Stasiak and Vsevolod Katritch, World Scientific Publishing Company, 414 pp.
- 2001, Knots and Physics (Series on Knots and Everything, Vol. 1), World Scientific Publishing Company, 788 pp.
- 2002, Hypercomplex Iterations: Distance Estimation and Higher Dimensional Fractals (Series on Knots and Everything , Vol 17), with Yumei Dang and Daniel Sandin.
- 2006, Formal Knot Theory, Dover Publications, 272 pp.
- 2007, Intelligence of Low Dimensional Topology 2006, with J. Scott Carter and Seiichi Kamada.
Articles and papers, a selection:
- 2001, The Mathematics of Charles Sanders Peirce, in: Cybernetics & Human Knowing, Vol.8, no.1–2, 2001, pp. 79–110
External links
- Louis Kauffman Homepage at uic.edu.
- http://www.evl.uic.edu/hypercomplex/ Hypercomplex Fractals.
- http://front.math.ucdavis.edu/search?a=louis+kauffman&t=&q=&c=&n=25&s=Listings Arxiv Papers.
- http://chickenfat.bandcamp.com/album/chickenfat-demos ChickenFat Klezmer Orchestra.