
Bracket polynomial
Encyclopedia
In the mathematical
field of knot theory
, the bracket polynomial (also known as the Kauffman bracket) is a polynomial
invariant of framed links. Although it is not an invariant of knots or links (as it is not invariant under type I Reidemeister move
s), a suitably "normalized" version yields the famous knot invariant
called the Jones polynomial. The bracket polynomial plays an important role in unifying the Jones polynomial with other quantum invariant
s. In particular, Kauffman's interpretation of the Jones polynomial allows generalization to invariants of 3-manifold
s.
The bracket polynomial was discovered by Louis Kauffman
in 1987.
The pictures in the second rule represent brackets of the link diagrams which differ inside a disc as shown but are identical outside. The third rule means that adding a circle disjoint from the rest of the diagram multiplies the bracket of the remaining diagram by -A2 - A-2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the bracket polynomial (also known as the Kauffman bracket) is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
invariant of framed links. Although it is not an invariant of knots or links (as it is not invariant under type I Reidemeister move
Reidemeister move
In the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
s), a suitably "normalized" version yields the famous knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
called the Jones polynomial. The bracket polynomial plays an important role in unifying the Jones polynomial with other quantum invariant
Quantum invariant
In the mathematical field of knot theory, a quantum invariant of a knot or link is a linear sum of colored Jones polynomial of surgery presentations of the knot complement.-List of invariants:*Finite type invariant*Kontsevich invariant*Kashaev's invariant...
s. In particular, Kauffman's interpretation of the Jones polynomial allows generalization to invariants of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s.
The bracket polynomial was discovered by Louis Kauffman
Louis Kauffman
Louis H. Kauffman is an American mathematician, topologist, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago...
in 1987.
Definition
The bracket polynomial of any (unoriented) link diagram L, denoted <L>, is characterized by the three rules:-
= 1, where O is the standard diagram of the unknot -
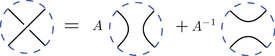
-
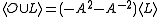
The pictures in the second rule represent brackets of the link diagrams which differ inside a disc as shown but are identical outside. The third rule means that adding a circle disjoint from the rest of the diagram multiplies the bracket of the remaining diagram by -A2 - A-2.

