Reidemeister move
Encyclopedia
In the mathematical
area of knot theory
, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister
and independently, in 1927, J.W. Alexander and G.B. Briggs, demonstrated that two knot diagrams belonging to the same knot, up to planar isotopy, can be related by a sequence of the three Reidemeister moves.
Each move operates on a small region of the diagram and is one of three types:
No other part of the diagram is involved in the picture of a move, and a planar isotopy may distort the picture. The numbering for the types of moves corresponds to how many strands are involved, e.g. a type II move operates on two strands of the diagram.
One important context in which the Reidemeister moves appear is in defining knot invariants. By demonstrating a property of a knot diagram which is not changed when we apply any of the Reidemeister moves, an invariant is defined. Many important invariants can be defined in this way, including the Jones polynomial.
The type I move is the only move that affects the writhe
of the diagram. The type III move is the only one which does not change the crossing number of the diagram.
In applications such as the Kirby calculus
, in which the desired equivalence class of knot diagrams is not a knot but a framed link, one must replace the type I move with a "modified type I" (type I') move composed of two type I moves of opposite sense. The type I' move affects neither the framing of the link nor the writhe of the overall knot diagram.
Bruce Trace showed that two knot diagrams are related by using only type II and III moves if and only if they have the same writhe
and winding number
. Furthermore, combined work of O. Östlund, V. O. Manturov, and T. Hagge shows that for every knot type there are a pair of knot diagrams so that every sequence of Reidemeister moves taking one to the other must use all three types of moves. Alexander Coward demonstrated that for link diagrams representing equivalent links, there is a sequence of moves ordered by type: first type I moves, then type II moves, type III, and then type II. The moves before the type III moves increase crossing number while those after decrease crossing number.
Joel Hass and Jeffrey Lagarias
proved the existence of an exponential upper bound (depending on crossing number) on the number of Reidemeister moves required to change a diagram of the unknot to the standard unknot. This gives an inefficient algorithm to solve the unknotting problem
. A weaker bound was announced by Galatolo around the same time.
Chuichiro Hayashi proved there is also an upper bound, depending on crossing number, on the number of Reidemeister moves required to split a link
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister
Kurt Reidemeister
Kurt Werner Friedrich Reidemeister was a mathematician born in Braunschweig , Germany.He received his doctorate in 1921 with a thesis in algebraic number theory at the University of Hamburg under the supervision of Erich Hecke. In 1923 he was appointed assistant professor at the University of Vienna...
and independently, in 1927, J.W. Alexander and G.B. Briggs, demonstrated that two knot diagrams belonging to the same knot, up to planar isotopy, can be related by a sequence of the three Reidemeister moves.
 |
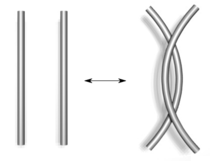 |
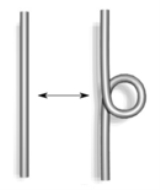
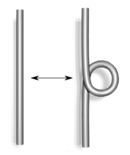
| Type I | Type II |
 |
|
| Type III | |
Each move operates on a small region of the diagram and is one of three types:
- Twist and untwist in either direction.
- Move one loop completely over another.
- Move a string completely over or under a crossing.
No other part of the diagram is involved in the picture of a move, and a planar isotopy may distort the picture. The numbering for the types of moves corresponds to how many strands are involved, e.g. a type II move operates on two strands of the diagram.
One important context in which the Reidemeister moves appear is in defining knot invariants. By demonstrating a property of a knot diagram which is not changed when we apply any of the Reidemeister moves, an invariant is defined. Many important invariants can be defined in this way, including the Jones polynomial.
The type I move is the only move that affects the writhe
Writhe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
of the diagram. The type III move is the only one which does not change the crossing number of the diagram.
In applications such as the Kirby calculus
Kirby calculus
In mathematics, the Kirby calculus in geometric topology, named after Robion Kirby, is a method for modifying framed links in the 3-sphere using a finite set of moves, the Kirby moves...
, in which the desired equivalence class of knot diagrams is not a knot but a framed link, one must replace the type I move with a "modified type I" (type I') move composed of two type I moves of opposite sense. The type I' move affects neither the framing of the link nor the writhe of the overall knot diagram.
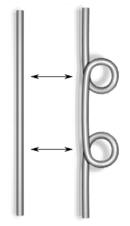 |
| Type I' |
Bruce Trace showed that two knot diagrams are related by using only type II and III moves if and only if they have the same writhe
Writhe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
and winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
. Furthermore, combined work of O. Östlund, V. O. Manturov, and T. Hagge shows that for every knot type there are a pair of knot diagrams so that every sequence of Reidemeister moves taking one to the other must use all three types of moves. Alexander Coward demonstrated that for link diagrams representing equivalent links, there is a sequence of moves ordered by type: first type I moves, then type II moves, type III, and then type II. The moves before the type III moves increase crossing number while those after decrease crossing number.
Joel Hass and Jeffrey Lagarias
Jeffrey Lagarias
Jeffrey Clark Lagarias is a mathematics professor at the University of Michigan.- Education :While in high school in 1966, Lagarias studied astronomy at the Summer Science Program....
proved the existence of an exponential upper bound (depending on crossing number) on the number of Reidemeister moves required to change a diagram of the unknot to the standard unknot. This gives an inefficient algorithm to solve the unknotting problem
Unknotting problem
In mathematics, the unknotting problem is the problem of algorithmically recognizing the unknot, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms...
. A weaker bound was announced by Galatolo around the same time.
Chuichiro Hayashi proved there is also an upper bound, depending on crossing number, on the number of Reidemeister moves required to split a link
Split link
In the mathematical field of knot theory, a split link is a link that has a 2-sphere in its complement separating one or more link components from the others. A split link is said to be splittable, and a link that is not split is called a non-split link or not splittable...
.

